Orbit 9-12-2020
A particle of mass M = 1 0 is fixed at the origin. At time t = 0 , another particle of mass m = 1 begins with position ( x , y ) = ( 1 , 0 ) and velocity ( x ˙ , y ˙ ) = ( − 2 , 2 ) . The universal gravitational constant G = 1 .
At time t = 5 , how far away is the moving particle from the origin?
Note: This one is surprisingly badly behaved, so make sure to do proper time-step convergence testing if solving numerically
The answer is 0.788.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Krishna Karthik
very nice solution.
Is the solution incomplete with that above image?
Log in to reply
Yes, it is incomplete without the guy. Michael Rosen's a legend.
"Hot food!"
@Lil Doug btw I thought you had a date? Lol
Log in to reply
@Krishna Karthik she is busy. We have decided it to tomorrow.
Log in to reply
@Talulah Riley – Lol. How did you start dating her? Did you just ask her out like that?
@Lil Doug btw did you solve the problem? How did you solve the differential equation?
Log in to reply
@Krishna Karthik i reached that two coupled differential equation after that I am unable to solve them.
Log in to reply
@Talulah Riley – But how did you get the answer then? Who is the second solver, if that is the case that you didn't solve it?
Log in to reply
@Krishna Karthik – @Krishna Karthik i don't know. Maybe Karan sir the ultimate Legend.
Log in to reply
@Talulah Riley – Yeah. He's always the first solver, isn't he? Lol.
Log in to reply
@Krishna Karthik – @Krishna Karthik in 90% cases he is the 1st solver.
Coupled equations are too hard to solve by hand. Better if you learn how to do it using code.
Well done! There is a typo in your equations of motion. A negative sign is missing.
Using polar coordinates, we can write
r ( t ) = ( x , y ) = r ( cos θ , sin θ )
Differentiating with respect to time t ,
r ˙ = r ˙ ( cos θ , sin θ ) + r ( − sin θ , cos θ ) θ ˙
Differentiating again,
r ¨ = r ¨ ( cos θ , sin θ ) + 2 r ˙ ( − sin θ , cos θ ) θ ˙ + r ( − cos θ , − sin θ ) ( θ ˙ ) 2 + r ( − sin θ , cos θ ) θ ¨
The force acting on the particle is F = r 2 − 1 0 ( cos θ , sin θ ) = m r ¨
Equating radial and traverse components of the vectors, on both sides of the equation, we deduce that,
r ¨ − r ( θ ˙ ) 2 = r 2 − 1 0 ( 1 )
and
2 r ˙ θ ˙ + r θ ¨ = 0 ( 2 )
Multiplying the second equation by r , we get,
2 r r ˙ θ ˙ + r 2 θ ¨ = 0 ( 3 )
The left hand side is just the derivative of r 2 θ ˙ , therefore,
r 2 θ ˙ = K ( 4 )
To determine K, we use the initial conditions, we're given that r ( 0 ) = 1 , θ ( 0 ) = 0 , r ˙ = ( − 2 , 2 ) , Using the expression for velocity developed above, we have,
r ˙ = r ˙ ( cos θ , sin θ ) + r ( − sin θ , cos θ ) θ ˙
so that,
( − 2 , 2 ) = r ˙ ( 1 , 0 ) + ( 1 ) ( 0 , 1 ) θ ˙
Therefore, r ˙ ( 0 ) = − 2 , and θ ˙ ( 0 ) = 2 , and it follows from this that the constant K = 2 . Plugging in equation (4) into (1),
r ¨ − r 3 4 = − r 2 1 0 ( 5 )
By relating the time-derivative of r to the θ -derivative, equation (5) becomes,
r 4 4 r ′ ′ − r 5 8 r ′ 2 − r 3 4 = − r 2 1 0 ( 6 )
where r ′ = d θ d r and r ′ ′ = d θ 2 d 2 r .
Now, we will use the change of variables, u = r 1 . This will change equation ( 6 ) into,
4 u ′ ′ + 4 u − 1 0 = 0 ( 7 )
where u ′ ′ = d θ 2 d 2 u . Equation ( 7 ) is a linear differential equation with constant coefficients. Dividing by 4,
u ′ ′ + u − 2 5 = 0 ( 8 )
The solution of this differential equation is:
u = 2 5 + A cos θ + B sin θ
Since r ( 0 ) = 1 , then , u ( 0 ) = 1 , and therefore, A = − 2 3 , and one can show that u ( 0 ) = 1 , hence B = 1 . And therefore,
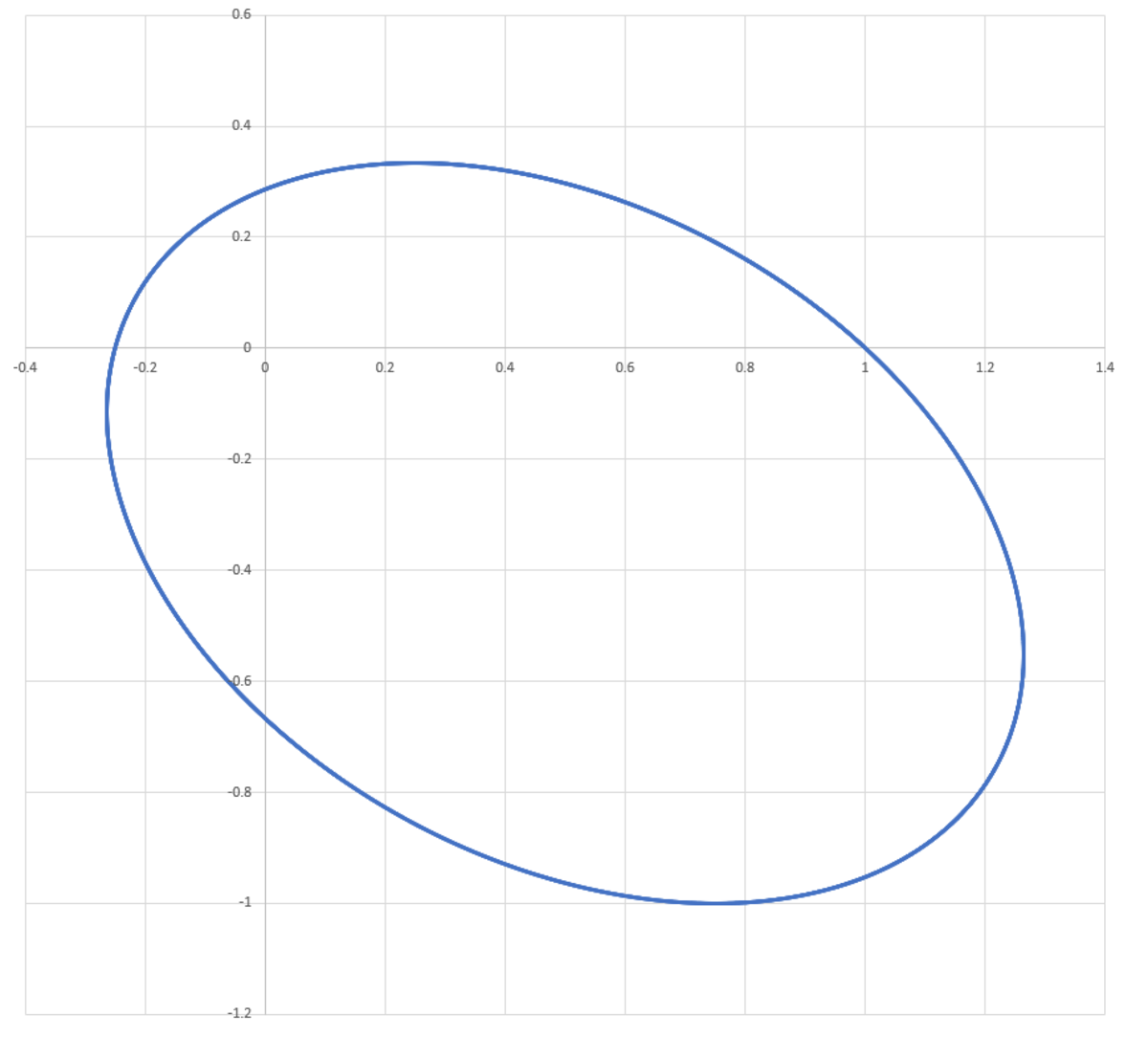
r ( θ ) = 2 5 − 2 3 cos θ + sin θ 1 ( 9 )
This is an equation of an ellipse. Now from equation (4), we have,
d t d θ = θ ˙ = r 2 2 = 2 ( 2 5 − 2 3 cos θ + sin θ ) 2
And this is a first-order differential equation in θ , which we want to integrate over [ 0 , 5 ] . For this I used the Runge-Kutta 4th-order method, with a step-size of h = 1 0 − 4 , I got θ ( 5 ) = 2 3 . 7 2 5 radians. Plugging this value for θ into equation ( 9 ) , gives r = 0 . 7 8 7 6 .
@Hosam Hajjir
You are on fire.
Very very very nice solution.
I was searching for this only. Upvoted.
Log in to reply
Yeah. See, if you want to avoid a coupled system, this is the way to go @Lil Doug .
Nice solution.
Thanks for the complement.
You're first solver, eh? I like how you used a different method to get an easier differential equation. Brilliant indeed.
@Krishna Karthik Hosam sir always rocks with his sttuborn anaylitical solutions.
Log in to reply
@Lil Doug Wait a minute... I just read that he used Runge-Kutta 4. Eitherway, he reduced a coupled system into a first order differential equation, which is still admirable.
It's still not fully analytical, though. I'm sure Mark Hennings will come up with something lol
Log in to reply
@Krishna Karthik yeah it is still admirable. Bye
@Hosam Hajjir i think you deleted the problem Ladder dynamics.
I've reposted it now.
I solved the problem using a Lagrangian approach. The Newtonian approach would be less straightforward and possibly harder. With this, I just yielded a system of equations, and numerically solved.
In Hossam's solution, a first order equation was produced using a lot of mathematical manipulation. In the end, Hossam's equation of motion is far better behaved and easier to numerically solve than the coupled system below.
With the system, there are 2 generalised coordinates, hence two coupled differential equations will result.
Later, I might try using generalised polar coordinates r and θ , and solve the Euler-Lagrange equation for them.
It may lead to a first order equation, actually.
So, the Euler-Lagrange equations for this system is given by:
d t d ( ∂ x ˙ ∂ L ) = ∂ x ∂ L
d t d ( ∂ y ˙ ∂ L ) = ∂ y ∂ L
The Lagrangian for the system can be found by finding the kinetic energy (the easy part) and the potential energy (the slightly harder part).
The gravitational potential energy can be found by:
U g = − r G M m
Where r is the distance from the origin. This distance can be found with a bit of Pythagoras:
r = x 2 + y 2
The Lagrangian:
L = 2 x ˙ 2 + 2 y ˙ 2 − x 2 + y 2 1 0
Solving the Euler-Lagrange equation will give:
x ¨ = − ( x 2 + y 2 ) 2 3 1 0 x
y ¨ = − ( x 2 + y 2 ) 2 3 1 0 y
The system is kind of badly behaved, even when you solve with a small timestep. But a timestep of 1 0 − 6 is enough to give you a good result.
Here's code if you want to see how I solved the coupled equation @Lil Doug