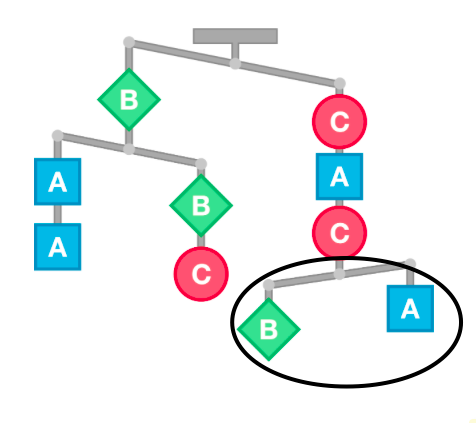
Order those Weights.

Geometry Level 1

Order the shapes from lightest to heaviest.

A < B < C A<B<C A < C < B A<C<B B < A < C B<A<C C < A < B C<A<B C < B < A C<B<A

Hana Wehbi by Hana Wehbi , 51, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

10 solutions

Chew-Seong Cheong
Apr 12, 2018

Relevant wiki: Linear Inequalities Word Problems

The right bottom balance indicates that A < B A<B .

The top balance indicates that

2 A + 2 B + C < 2 A + B + 2 C 2 A + 2 B + C < 2 A + B + 2 C 2 B − B < 2 C − C ⟹ B < C \begin{aligned} 2A+2B + C & < 2A+B+2C \\ \cancel{2A} + 2B + C & < \cancel{2A}+B+2C \\ 2B - B & < 2C - C \\ \implies B & < C \end{aligned}

Therefore, A < B < C \boxed{A<B<C} .

122 Helpful 0 Interesting 0 Brilliant 0 Confused

Doesn't necessarily mean that C > B. But if you count left and right you will see there's 1 B more left and 1 C more right(next to the 2 A's, 1B and 1 C om both sides). Hence B<C.

Peter van der Linden - 3 years, 2 months ago

Log in to reply

The inequality actually do the balancing.

Chew-Seong Cheong - 3 years, 2 months ago

Note: there is one more inequality that can be written 2 A < B + C 2A<B+C but nothing can be deduced about C C from it.

Jeremy Galvagni - 3 years, 1 month ago

That's not enough. So far you've only proved that B > A. There's more than that.

Pedram Ardakani - 3 years, 1 month ago

Log in to reply

The top balance indicates that

2 A + 2 B + C < 2 A + B + 2 C 2 A + 2 B + C < 2 A + B + 2 C 2 B − B < 2 C − C ⟹ B < C \begin{aligned} 2A+2B + C & < 2A+B+2C \\ \cancel{2A} + 2B + C & < \cancel{2A}+B+2C \\ 2B - B & < 2C - C \\ \implies B & < C \end{aligned}

Chew-Seong Cheong - 3 years, 1 month ago
Inksa Inkeroinen
Apr 30, 2018

My solution is totally pictorial. First, A < B : A<B:

Then, let's remove 2 A , B 2A, B and C C from both sides:

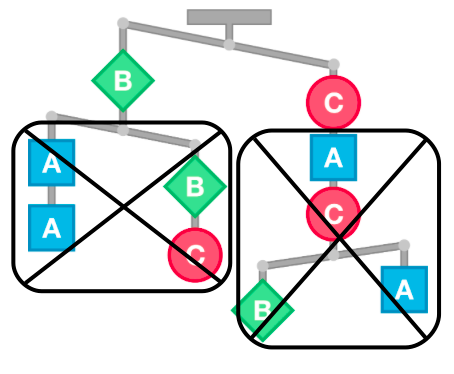
So, B < C B<C

Finally, combining both pictures we get A < B < C \boxed{A<B<C}

91 Helpful 0 Interesting 1 Brilliant 0 Confused

Draw a bit bettar!!!!!!

Ashab Jahin - 3 years, 1 month ago

Log in to reply

I have tried now. Hope it's a bit better! :)

Inksa Inkeroinen - 3 years, 1 month ago

it's a very elegant proof!

Austin David - 3 years, 1 month ago

Can you really do it this way? For example, the two C:s are not on the same distance from the center of the balance.

Stefan Pohl - 3 years, 1 month ago

Log in to reply

Without actually being told we are assuming that the weights are equal distances on each side (otherwise you can't really solve the problem). Therefore each set of weights is acting the same distance from center (it doesn't matter where they are positioned on the lower bars, the lower weights are all acting on the same point of the upper bar).

Chris Cheek - 3 years, 1 month ago

I just assume that removing same things from different sides of the balance doesn't change the equilibrium.

Inksa Inkeroinen - 3 years, 1 month ago

Log in to reply

It doesn't, as long as they are acting at the same distance from center.

Chris Cheek - 3 years, 1 month ago

Log in to reply

@Chris Cheek – I see, you're right. We only have to assume that the sides of the upper bar are equally length. As you described below.

Inksa Inkeroinen - 3 years, 1 month ago

A very elegant proof.

Rajath Pai - 3 years, 1 month ago
Daniel Maher
Apr 29, 2018

In the lower right corner of the picture, it shows 1 A weighed against 1 B. Since the B is lower, A < B. Both sides of the overall balance have 2 A's, and at least 1 B and C. However, the left side has an additional B, and the right side has an additional C. The C side is lower, so B < C. In the end, it's A < B < C.

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Clean reasoning indeed

Agnishom Chattopadhyay - 3 years, 1 month ago
Corbin Lambert
May 4, 2018

Lol I'm 11 and did a quiz and got all right I'm smart

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Justin Chung
May 6, 2018

This diagrams depicts that 2A + 2B + C < 2A + B + 2C. We can simplify this to B < C. The scale on the bottom of the right side of the big scale shows that A < B. Therefore, A<B<C.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

B > A

2A + B +2C > 2A + 2B + C

2A - 2A + 2C - C > 2B - B

C > B

Therefore: C > B > A

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Conclusion from the right end : B bigger than A And when solve the hall system which is ( right) 2c+2a+b > 2a+ 2b+c ( left) Result : c> b and already known b>a Total : c>b>a

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Aayush Karn
May 2, 2018

Well I got the answer in a bit different way. Firstly, look at the last balance in the left side where there are two As against a B and a C combined. From this, we can say that 2A<B+C (or) A<(B+C)/2 This means that A is even lighter than the mean of the other two blocks. So one can make a guess that A is the lightest. This can even be confirmed by looking at the last balance of the right side where clearly B is more heavier than A. So for the time being we can write. A<B Now in the main balance, there are two Bs in the left side and 2 Cs in the right side and we can see that the right side is more dominating the left side. This means that C>B. And from our last two expressions we get that A is the least heaviest of all. So, A<B<C.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Rahul GAutam
May 1, 2018

1.B>A 2.2A+2C+B>2B+2A+C :- 2C+B>2B+C :-C>B THEREFORE- A<B<C

0 Helpful 0 Interesting 0 Brilliant 0 Confused
한얼 이
Apr 30, 2018

A < B,

2A + 2B + C < 2A + B + 2C

2A - 2A + 2B - B < 2C - C

B < C

So, A < B < C

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I have a question!!!! who can tell me why the A and B in bottom of the right side can keep balance. their weights are different, but the distance to the fulcrum are the same(no matter the lever has been tilted or not). that's means their moments are different. So how can the leverage keep balance???

云修 马 - 3 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...