Oscillation Frequencies...
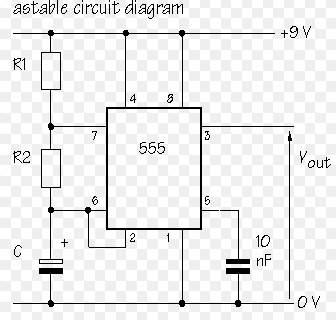 I have an Astable 555 Timer set up as shown above. What is the value of
R
1
(in
k
Ω
) to generate a pulse of 37.7 [Hz] with a pause of 0.0265 [s] per wave, given that the value of
R
2
is 15
k
Ω
and the value of
C
1
is 1
µ
F
?
I have an Astable 555 Timer set up as shown above. What is the value of
R
1
(in
k
Ω
) to generate a pulse of 37.7 [Hz] with a pause of 0.0265 [s] per wave, given that the value of
R
2
is 15
k
Ω
and the value of
C
1
is 1
µ
F
?
Give your answer to 1 d.p. Calculators ARE ALLOWED. If you want to challenge yourself don't use one!
The answer is 8.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This question requires the use of the formula for the frequency of pulses which is :
f = ( R 1 + 2 R 2 ) × C 1 . 4 4
In the frequency calculation, if the units k Ω and μF are used. The output frequency will be in kHz. The question states that:
- R 1 is unknown
- R 2 is 15k Ω
- C 1 is 1μF
- The frequency ( f ) is 37.7 Hz
To enable us to get a correct answer, we need to convert the frequency of 37.7Hz to kHz since we will be using k Ω and μF. If you need additional clarification look at the table on this page.
To convert Hz to kHz we ÷ 1 0 0 0 . So...
- 37.7Hz = 0.0377 kHz
Lets re-arrange to get the value of R 1 :
R 1 = f × C 1 . 4 4 − 2 R 2
Substitute into the formula:
- R 1 = 0 . 0 3 7 7 k H z × 1 μ F 1 . 4 4 − 2 ( 1 5 k Ω )
Which gives us 8.196 , rounded to 1 d.p which is 8 . 2 k Ω
Note: The time period is not used here. It is not required since we are only looking for the frequency which has a direct influence on the time delay between each pulse.
well done with your solution. i solved it using the same way. except i didn't convert them all into khz and stuff like that...i did it at the end
Log in to reply
Well Done Kunal! Yes, that's the alternative way of doing it...
Log in to reply
by the way...you're solution is wrong. you've written 8.2 ohm instead of 8.2 kilo ohm
Log in to reply
@Kunal Jadhav – SIMPLE MISTAKE!!!!
Log in to reply
@Kavinda Jayasinghege Don – you're still wrong you faker
Before we begin, we normalize all voltage, currents, time and elements by the values given below: voltages: 1 V , currents: 1 m A , time: 1 m s , ⇒ R : 1 k Ω , C : 1 μ F , f : 1 k H z The network equations remain the same in the process, but now all variables represent their normalized, dimensionless counterparts.
Short solution
A quick look into an (old) datasheet for the N*555* yields the formula between frequency and element values on page 11 (astable timer mode): f = ln ( 2 ) ( R 1 + 2 R 2 ) C 1 ≈ ( R 1 + 2 R 2 ) C 1 . 4 4 ⇒ R 1 = ln ( 2 ) f C 1 − 2 R 2 = ln ( 2 ) ⋅ 3 7 . 7 × 1 0 − 3 1 − 3 0 ≈ 8 . 2 ( ∗ )
Longer solution
You think just using the frequency formula feels like cheating? Let's analyze how the circuit actually works - another look into the datasheet for the N*555* tells us which pins of the IC are relevant here. The pins for trigger- and threshold-voltage ( pin 2 and pin 6 ) are shorted, so the IC-logic simplifies to
All pin voltages u k ( t ) are measured from pin to ground.
Let's assume the network was de-energized and we switch on the supply voltage V c c = 9 . Then the network will go through three distinct stages:
To calculate T 0 , T 1 , we need to analyze two basic RC-circuits with different resistors and initial conditions. Using KVL and defining i C ( t ) as the current through C from top to bottom, we get the following ODEs. We also shift time such that the initial conditions are set at t = 0 in both cases: T 0 : T 1 : 0 0 = R 2 i C ( t ) + u 2 ( t ) = R 2 C u 2 ( 1 ) ( t ) + u 2 ( t ) = − V c c + ( R 1 + R 2 ) i C ( t ) + u 2 ( t ) = − V c c + ( R 1 + R 2 ) C u 2 ( 1 ) ( t ) + u 2 ( t ) ⇒ ⇒ u 2 ( 1 ) ( t ) u 2 ( 1 ) ( t ) = − A 0 u 2 ( t ) , = − A 1 u 2 ( t ) + 9 A 1 , u 2 ( 0 ) u 2 ( 0 ) = 6 = 3 The new short-hands are A 0 : = R 2 C 1 , A 1 : = ( R 1 + R 2 ) C 1 . Solving both ODEs, we can calculate T 0 , T 1 and finally the period T = f 1 of the output u 3 ( t ) : T 0 : T 1 : u 2 ( T 0 ) u 2 ( T 1 ) = 6 e − A 0 T 0 = ! 3 = 9 − 6 e − A 1 T 1 = ! 6 ⇒ ⇒ T 0 T 1 = ln ( 2 ) R 2 C = ln ( 2 ) ( R 1 + R 2 ) C ⎭ ⎪ ⎬ ⎪ ⎫ ⇒ T = T 0 + T 1 = ln ( 2 ) ( R 1 + 2 R 2 ) C = ! f 1 , R 1 ( ∗ ) ≈ 8 . 2
Rem.: The value 2 6 . 5 m s given for "pause time per wave" is actually the period T = f 1 and not T 0 , as I thought at first.