Oscillation on inline
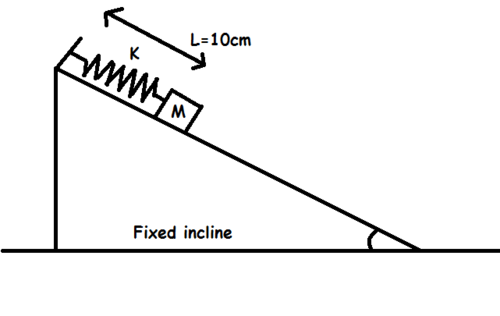 A block of mass M = 1 kg is placed of a fixed rough incline of inclination
θ
=
sin
−
1
1
0
7
and coefficient of friction
μ
=
5
1
1
connected to a spring of spring constant 100 N/m.
A block of mass M = 1 kg is placed of a fixed rough incline of inclination
θ
=
sin
−
1
1
0
7
and coefficient of friction
μ
=
5
1
1
connected to a spring of spring constant 100 N/m.
Initially the spring is in relaxed state with length = 10 cm. If the block is left to move, then, find the increment in the length (in cms) in spring when block is completely at rest .
Take g = 1 0 m/s 2 .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since the solution directly below mine is slightly flawed, I have posted a code solution just to make sure.
So, the gravitational force acting on the block in the ramp's direction is:
F g = m g sin ( θ )
Spring force:
F s = − k ( x − l )
Friction force:
F μ = ± μ m g cos ( θ )
The friction force depends on the direction of velocity. Programming all these forces into a Python simulation program, and calculating net force at each point, thereby calculating the acceleration, we can numerically integrate.
Here's the code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
|
As we can see, extending the time, the final elongation appears to be 8 centimeters.
As the block moves down the incline, the spring starts getting elongated.
At maximum elongation, the spring shall have the tendency to move the block upwards ( or towards the spring's equilibrium position). We know force component mg sin theta shall act downwards the incline. Now since the block has tendency to move upwards, the friction force shall be acting downwards the incline.
Hence, kx = mg sin theta + f ; f is the force of friction at that instant.
Therefore, f = kx - mg sin theta
We know f is smaller than equal to its limiting value, which is equal to umg cos theta for an inclined plane situation.
OR kx - mg sin theta = f ( instant ) <= f ( limiting ) <= u mg cos theta
OR
kx <= u mg cos theta + mg sin theta
Solve the equation to obtain the maximum elongation.
You made a wrong assumption that the friction force will have its limiting value which may not be true. The block can also come to rest with the friction force acting downward and having a value less than its maximum.
Log in to reply
is it even correct now+i think you should remove certain things from the q like make ans 8.000(as decimals) because it easier to crack it now and also remove the word elongation let it be to us to think that next i would love to have a proper sol.
how will you proceed through the question
oh! so completely at rest means equilibrium, thought it was extreme!! :( nice one!
Log in to reply
Same thoughts! But later my friend @Thomas Jacob said, its not so
Log in to reply
Then how to proceed through the question
Can we do it by energy conservation ?
Log in to reply
Actually no. As in energy, u don't get a place where both accln and velocity is zero
Log in to reply
Then without using energy conservation how can you solve the question
Let x denote the block's position on the incline relative to its starting position with positive values denoting positions down the wedge. In the x -direction, the block experiences three forces: a component of its weight M g sin θ , the tension in the spring − k x , and friction, which has magnitude μ M g cos θ and initially acts in the same direction as the spring. Let x 1 denote the block's position at the bottom of its first oscillation. At x = 0 , the block has 0 velocity, and from x = 0 to x = x 1 , the net work of gravity, the spring, and friction is 0 because the block again has 0 velocity. This means ∫ 0 x 1 ( M g sin θ − μ M g cos θ − k x ) d x = 0 and thus x 1 = k 2 M g ( sin θ − μ cos θ ) . At this point, the block's velocity and friction change directions. Let x 2 denote the position of the block at the top of the first oscillation. By the same argument as before, the work integral (with friction acting in the same direction as gravity) must again equal 0, so ∫ x 1 x 2 ( M g sin θ + μ M g cos θ − k x ) d x = 0 ⟹ x 2 = − x 1 + k 2 M g ( sin θ + μ cos θ ) . In general, if x n denotes the block's position the n th time it comes to rest, then x n + 1 = − x n + k 2 M g [ sin θ + ( − 1 ) n + 1 μ cos θ ] . This recurrence relation continues to hold until the block comes to rest at some x n where the magnitude of the combined force from gravity and the spring, ∣ M g sin θ − k x n ∣ , is less than or equal to the magnitude of the friction force, μ M g cos θ . When this happens, gravity and the spring can no longer overcome friction, so the block remains completely at rest. In this particular case, this happens at x 3 . Taking x 0 = 0 and applying the recurrence relation three times gives the values x 1 = k 2 M g ( sin θ − μ cos θ ) = 0 . 1 2 m , x 2 = − x 1 + k 2 M g ( sin θ + μ cos θ ) = 0 . 0 4 m , x 3 = − x 2 + k 2 M g ( sin θ − μ cos θ ) = 0 . 0 8 m . Therefore, the block's final position is x 3 = 0 . 0 8 m from its starting position, where the spring is stretched by 8 c m .