Small Ring Oscillation
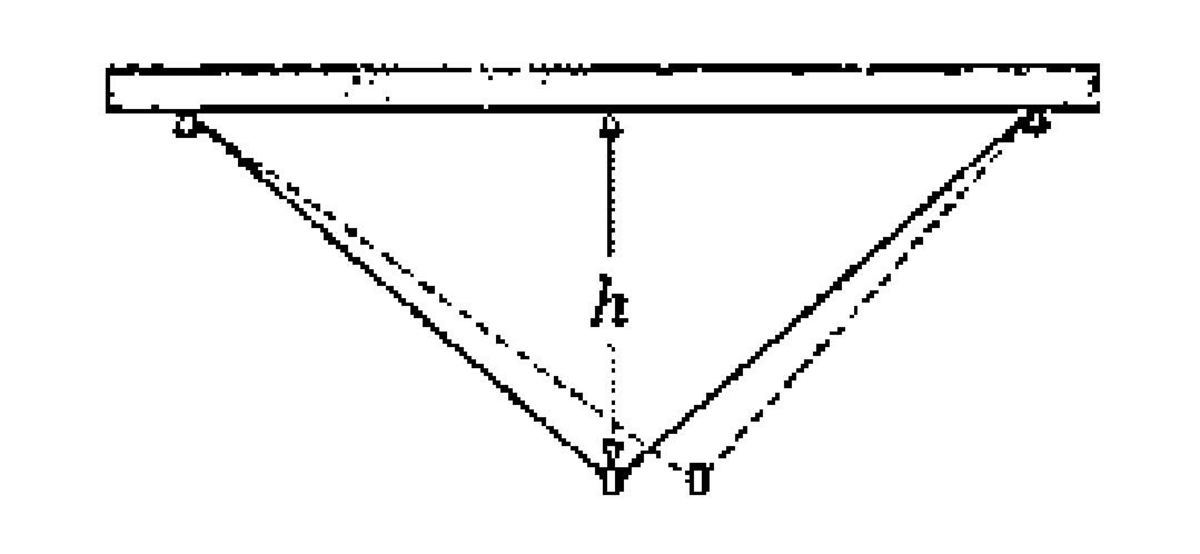 A small ring is threaded on an inextensible frictionless cord of length
2
l
. The ends of the cord are fixed to a horizontal ceiling. In equilibrium, the ring is at a depth
h
below the ceiling. Now the ring is pulled aside by a small distance in the vertical plane containing the cord and released.
Find period of small oscillations of the ring. Acceleration of free fall is
g
.
A small ring is threaded on an inextensible frictionless cord of length
2
l
. The ends of the cord are fixed to a horizontal ceiling. In equilibrium, the ring is at a depth
h
below the ceiling. Now the ring is pulled aside by a small distance in the vertical plane containing the cord and released.
Find period of small oscillations of the ring. Acceleration of free fall is
g
.
α
l
g
h
1
Type
α
+
1
−
5
+
2
2
The answer is 6.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Mark Hennings Thanks for the solution. Upvoted.
@Mark Hennings By the way congratulations for 17k problems solved.
@Mark Hennings if I would take + h cos θ instead of − h cos θ then my θ will he 2 7 0 ° . Am I right?
@Mark Hennings
Your solution is so sweet and small and explanatory.
You should at least awarded a Nobel Prize in Physics.
Log in to reply
Glad you like it. As a mathematician, I could never aspire to a Nobel prize, even if I were good enough (I am not!) - they don't give them for mathematics. If I can persuade you, and others, to perform some analysis before reaching for a computer to code the solution, I will be happy.
Log in to reply
@Mark Hennings So basically you want to say that we should try a problem anaylitcally before going for computer to code the solution. Am I right?
Log in to reply
@Talulah Riley – You've got it. You can write down the equations, and let the computer give you an (approximate) solution. Alternatively, you can solve those equations, and really know what is going on, and why.
Log in to reply
@Mark Hennings – @Mark Hennings Are you more of a mathematician, or a physicist?
Log in to reply
@Krishna Karthik – I am a Pure Mathematician by training. I have researched on the Pure Mathematics behind quantum mechanics, but I have not been in a lab since I was at school. You might best describe me as someone interested in the mathematics of theoretical physics.
Log in to reply
@Mark Hennings – That's pretty cool. Did you do any math competitions when you were younger?
@Mark Hennings – Btw I agree; I really need to develop my ability to use pure mathematics to solve physics problems. Computers have their uses, but an analytical idea is the thing that develops the physical theories.
Btw great solution. I reached for the computer a little too early with this one.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
yeah I agree with you.
By the way, What is the wrong with mathematics, people should also get Nobel Prize in that.
Log in to reply
@Talulah Riley – There is already a prize for that. It's called the "Fields Medal". It is the equivalent of a Nobel prize for mathematics.
I derived a solution method for arbitrarily large oscillations, and then simulated some small oscillations as special cases. The sum of the distances from the ring to the two points is a constant. It therefore follows that the ring is confined to an ellipse, and the two anchor points are the ellipse foci:
A x 2 + B y 2 = 1 A = ℓ 2 1 B = h 2 1
Derive an acceleration constrain equation:
A x 2 + B y 2 = 1 A x x ˙ + B y y ˙ = 0 A ( x x ¨ + x ˙ 2 ) + B ( y y ¨ + y ˙ 2 ) = 0
Assuming the ring mass to be one, write the Newton's Second Law equations. In these equations, N is the magnitude of the normal force to the curve, and u = ( u x , u y ) is the unit normal vector:
x ¨ = N u x y ¨ = N u y − g
Plugging these into the acceleration constraint equation and solving yields:
N = A x u x + B y u y − A x ˙ 2 − B y ˙ 2 + B g y
Having solved for N , plug it back in to find the double-dot terms. Numerically integrate to simulate the dynamics. For small oscillations, the constant α = 2 π .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
|
@Steven Chase can we solve it analytically ?
Placing the coordinate origin halfway between the two suspension points, the ring moves one the ellipse ℓ 2 x 2 + h 2 y 2 = 1 with the two suspension points at the foci. If the ring is at the point with position vector r = ( ℓ sin θ − h cos θ ) then conservation of energy gives us that 2 1 m ( ℓ 2 cos 2 θ + h 2 sin 2 θ ) θ ˙ 2 − m g h cos θ is constant. Thus m ( ℓ 2 cos 2 θ + h 2 sin 2 θ ) θ ¨ − m ( ℓ 2 − h 2 ) sin θ cos θ θ ˙ 2 + m g h sin θ = 0 Linearising about the equilibrium position θ = 0 , we deduce that ℓ 2 θ ¨ + g h θ ≈ 0 and so we have small oscillations of period 2 π g h ℓ 2 and hence α = 2 π .