Oscillations of a tetra-atomic molecule
Consider the following model of a tetra-atomic molecule: Four point-charges with charge q and mass m are connected by light rigid rods of length l . Clearly, the molecule is in equilibrium when the charges form a square of side l . Since this equilibrium is stable, the molecule can oscillate as shown in the figure. If the parameters q , m , and l satisfy m l 3 k q 2 = 1 0 4 s − 2 where k = 4 π ϵ 0 1 , find the period T in seconds of small oscillations.
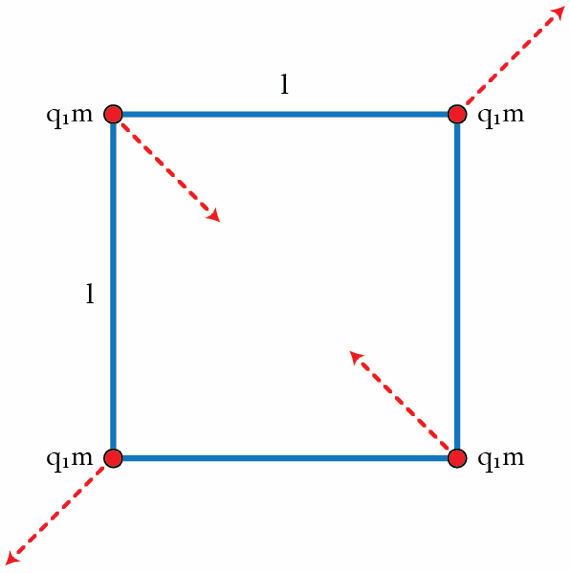
The answer is 0.0528.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
You don't mean an "infinitely small", or even an "infinitesimally small" distance. You mean a very small distance (so that second order effects can be ignored), giving approximate SHM.
Hello Jatin!
A similar problem was posted before ( click here ). I solved the problem by writing the energy of the system at any instant i.e E=K+U and differentiated wrt to time to obtain the time period of oscillation. Is it possible to apply the same method here? I hope you can help me out with this.
Thanks!
Log in to reply
See this method is exactly same as taing derivative of (K + U) ,but wrt x and not t .
Actually,
K + U = 2 1 m v 2 + U
d x d ( K + U ) = 0
⇒ m d x v d v + d x d U = 0 , F = d x − d U .
Here , in this question , due to symmetry, i could directly divide by four .Actually, i would derivate 4 K + U t o t a l wrt x to get that relation. But , there in your question i would be considering non- symmetrical factors and then would apply d x d ( α K + U t o t a l ) = 0 , where x is the displacement of a particular charge and K is the kinetic energy of that particular charge. α is a constant such that α K = K t o t a l . F = α − 1 d x d U . In present question , α = 4 .
I hope it helps. :)
Log in to reply
Great explanation Jatin! Thanks a lot! :)
Sorry to bother you again but can you please show your solution to the "Oscillation of triatomic molecule"?
I face trouble in finding the kinetic energy of system. If the vertical velocity of middle charge is v, the other two have v/2 in the opposite directions. How did you find the horizontal velocity of the other two charges? By equating the components along the rod? If so, can you please show the final expression you get for kinetic energy?
Any help is appreciated. Thanks!
Log in to reply
@Pranav Arora – Let the horizontal component of velocity of end charges is v 1 and vertical component is v 2 , velocity of mid charge be v 0 and the rod has rotated by small angle θ .Taking derivative , v 0 = 2 v 2 .Now,equating velocity component along the rod,
v 1 cos θ − v 2 sin θ = v 0 sin θ
v 1 = 3 v 2 tan θ < < v 2 .
Hence , the contribution of v 1 in kinetic energy would be negligible.
Now , v 2 can be replaced by v , the total velocity of end charges (as v 1 < < v 2 ).
velocity of mid charge = 2 v .
Hence , kinetic energy = 2 2 1 m v 2 + 2 1 m ( 2 v ) 2 = 3 m v 2 = 6 K . ⇒ α = 6 .
U s y s t e m = 2 l k q 2 + 2 l cos θ k q 2
= 2 l k q 2 + 2 l 2 − ( 3 x ) 2 k q 2 .
Already derived , F = − α 1 d x d U = − 6 1 4 l 3 1 8 k q 2 x = 4 l 3 3 k q 2 x
Hence , we deduce that T = 2 π 3 k q 2 4 m l 3 .
Again , i hope it helps.
Log in to reply
@Jatin Yadav – I must be an idiot but I don't see why the contribution due to v 1 is negligible.
I did reach to the point that v 1 = 3 v 2 tan θ . Why is v 1 much less than v 2? Is it because that the angle is very small and hence tan θ is small?
As always, help is appreciated. Thanks!
Log in to reply
@Pranav Arora – Of course because t a n θ = l 2 − 9 x 2 3 x is small, as x is small.
@Jatin Yadav – I didn't get how υ 0 = 2 υ 2 directly. What derivative did you take? Thanks anyways.
wow! great method of U and K . nicely explained. I always wondered how F = d x − d U .
Yes , mark.H , i actually meant small with respect to l , not infinitely small.
I don't see why you need to differentiate U to find force at all. Once you recognize that U is in the form of a spring potential, you simply need to extract the spring constant by inspection.
Hi Do you mind explaining how did you get from the first line to the second line for the last two terms? 2 ( a + x ) k q 2 + 2 ( a − x ) k q 2 to a k q 2 ( 1 + a 2 x 2 ) I couldn't work it out... Much appreciated :)
Log in to reply
2 ( a + x ) 1 + 2 ( a − x ) 1 = 2 ( a 2 − x 2 ) a + x + a − x = a 2 − x 2 a = ( a 1 ) ( a 2 − x 2 a 2 ) = ( a 1 ) ( 1 − a 2 x 2 1 ) = ( a 1 ) ( 1 − a 2 x 2 ) − 1
The key insight is that the displacement, x , is very small, so we may use the binomial approximation: ( 1 + ε ) α ≈ 1 + α ε . Thus: ( a 1 ) ( 1 − a 2 x 2 ) − 1 ≈ ( a 1 ) ( 1 + a 2 x 2 )
All you need to do is stick the k q 2 back in.
Suppose the distance from 2 opposite charges to the center of the system is a , from 2 other charges to the center is b . Hence, a 2 + b 2 = l 2 .
Therefore, 2 a Δ a + 2 b Δ b = 0 .
When the system is in equilibrium, a = b = 2 l . Therefore, with small oscillation, Δ a + Δ b = 0 or the displacement of all the charges are the same.
Suppose each charge is displaced by x .
The energy of the whole system is:
E = 4 2 m x ′ 2 + 4 l k q 2 + l 2 + 2 x k q 2 + l 2 − 2 x k q 2
= 2 m x ′ 2 + l 4 k q 2 + 2 l 2 − 4 x 2 2 2 l k q 2
≈ 2 m x ′ 2 + l 4 k q 2 + 2 l 2 2 2 l k q 2 ( 1 + 2 l 2 4 x 2 )
= 2 m x ′ 2 + l 4 k q 2 + l 2 k q 2 ( 1 + l 2 2 x 2 )
Since the energy of the system is constant, d t d E = 0
Hence, 4 m x ′ x ′ ′ + l 2 k q 2 l 2 4 x x ′ = 0
x ′ ′ + x m l 3 2 k q 2 = 0 .
Therefore, the period of the small oscillation is: T = 2 π 2 k q 2 m l 3 = 0 . 0 5 2 8 ( s ) .
Nicely done, thank you Dinh! I was wondering how would you approach the problem using the energy method. Your solution cleared the dilemma! Thank you. :)
In general, the four particles form a rhombus. Suppose that the lengths of the two diagonals of the rhombus are 2 x and 2 y , where x 2 + y 2 = ℓ 2 . Then the kinetic energy of the system is 2 1 m x ˙ 2 + 2 1 m x ˙ 2 + 2 1 m y ˙ 2 + 2 1 m y ˙ 2 = m ( x ˙ 2 + y ˙ 2 ) and the potential energy of the system is 2 x k q 2 + 2 y k q 2 Only the distances between the opposite pairs of particles change (the other four pairs of particles are all distance ℓ apart), and hence we only need to add their contribution to the potential energy equation. Thus m ( x ˙ 2 + y ˙ 2 ) + 2 x k q 2 + 2 y k q 2 = c for some constant c , and hence 2 m x ˙ x ¨ + 2 m y ˙ y ¨ − 2 x 2 k q 2 x ˙ − 2 y 2 k q 2 y ˙ = 0 Linearising this equation near the point of equilibrium we have x ≈ 2 ℓ + u , y ≈ 2 ℓ − u , where u ¨ + m ℓ 3 k q 2 2 u u ¨ + ( 2 × 1 0 4 ) u ≈ ≈ 0 0 giving SHM with approximate period of 2 π / 2 × 1 0 4 = 0 . 0 5 2 8 seconds.
Let us displace the charges along diagonals by a infinitely small distance x . Let U be the potential energy of system.Let a = 2 l
U = 4 l k q 2 + 2 ( a + x ) k q 2 + 2 ( a − x ) k q 2
= 4 l k q 2 + a k q 2 ( 1 + a 2 x 2 )
d x d U = a 3 2 k q 2 x = l 3 4 2 k q 2 x
F = 4 1 ( − d x d U ) = − l 3 2 k q 2 x
⇒ T = 2 π 2 k q 2 m l 3 = 0 . 0 5 2 8