Out shopping

Calculus Level 2

While shopping, you find an item with a random price evenly distributed between $0 and $60. You buy as many of these items as possible with the $60 you brought.

What is the expected amount of money you have spent (in dollars)?

Note: You may assume that $60 is large compared to a penny so that the distribution of prices is essentially continuous.

4.5\pi^2

5\pi^2

5.5\pi^2

6\pi^2

4 solutions

Mark Hennings
Aug 27, 2018

We want to calculate $E \; = \; \frac{1}{60}\int_0^{60} x \left\lfloor \tfrac{60}{x} \right\rfloor\,dx$ With the substitution $x = \tfrac{60}{y}$ , this becomes $\begin{aligned} E & = \; 60\int_1^\infty \frac{\lfloor y\rfloor}{y^3}\,dy \; = \; 60\sum_{n=1}^\infty n\int_n^{n+1} \frac{dy}{y^3} \; = \; 30\sum_{n=1}^\infty n\left(\frac{1}{n^2} - \frac{1}{(n+1)^2}\right) \\ & = \; 30\sum_{n=1}^\infty \left(\frac{1}{n} - \frac{1}{n+1} + \frac{1}{(n+1)^2}\right) \; = \; 30\left(1 + \sum_{n=2}^\infty \frac{1}{n^2}\right) \; = \; 30\zeta(2) \; = \; \boxed{5\pi^2} \end{aligned}$

That's a concise way of expressing the expected value that needs to be calculated. But it's interesting to see how you've gone about to evaulate that floor function. If one tries to put that integral in Wolfram Alpha, it won't return a value.

Michael Mendrin - 2 years, 9 months ago

It gives me a numerical answer accurate to $4$ SF which is, sadly, enough to get the correct answer for the question.

Making the argument of a floor function a simple variable, and then splitting the integral into strips of width $1$ , is the standard approach to handling integrals involving the floor function.

Mark Hennings - 2 years, 9 months ago

I'm consistently getting around 43 with MC.

Charlie Recchia - 2 years, 9 months ago

I imagine you are suffering from rounding errors. You are having to multiply things that can be very small, like $x$ , by things that can be very large, like the integer part of {60/x). Add to this the fact that small values of $x$ make an important contribution to the sum...

What happens if you try to calculate the $y$ integral instead?

Mark Hennings - 2 years, 9 months ago

Me too, numerically, by MC, I get something like 43.09. I have also developed a theoretical analysis, which is quite involved, that provides that the correct result is 60(e-2), where e is Neper number, and this is actually equal to 43.0969....

Stefano Micheletti - 2 years, 9 months ago

Well, I and Michael have both provided elementary proofs of the $5\pi^2$ result. If you want to post your calculations, I will critique them for you.

Mark Hennings - 2 years, 9 months ago

@Mark Hennings – I'll try to summarize my findings. I think that the main difference with respect to your and Michael's solutions is that in order to establish that it takes n draws of items not to spend more than $60, you need to also draw the (n+1)-item. Actually, this is what one would do when implementing a MC method: keep picking items until the total cost exceeds $60, say at the n+1 item, so that you actually can afford to buy only n items. Based on that, I first computed the distribution of probability of the number of items, i.e., p(n) = probability that it takes exactly n items not to exceed $60, provided that the total cost of n+1 items exceeds $60. Then I computed the mean cost associated with the different n, i.e., C(n) = mean cost spent by collecting n items, under the same conditions on n as for p(n). Finally, I computed the mean cost by summing the product p(n) C(n) for n>=1. The result of this computation is that the mean cost is $60(e - 2), where e is Neper number, which amounts to 43.0969. This value and also the distributions p(n) and C(n) match very well the MC results, beyond any reasonable doubt (I used 10^6 samples).

Stefano Micheletti - 2 years, 9 months ago

@Stefano Micheletti – You do not need to draw $n+1$ items to know whether you can pay for them or not - you know when you look at the first of these items what it costs, and so you can work out (by dividing the cost into $60$ and taking the integer part) exactly how many you can buy, since once the costs per item is established, all items cost the same.

The bottom line is that your MC method is probably not implementing a uniform distribution of costs. The cost of an item should be a continuous random variable $X$ with probability distribution function $f(x) \; = \; \left\{ \begin{array}{lll} \tfrac{1}{60} & \hspace{1cm} 0 < x < 60 \\ 0 & & \mathrm{o.w.}\end{array}\right.$ If you are going to apply a MC method here, you need to do something like this:

Take a random integer $N$ between $1$ and $1000000$ (say) inclusive (all equally likely), and calculate the cost $C = \frac{60N}{1000000}$ per item.
Calculate the number of items $\big\lfloor \tfrac{60}{C}\big\rfloor$ that can be bought at this cost, and calculate the total cost $T = C \times \big\lfloor \tfrac{60}{C}\big\rfloor$ .
Do this a large number of times and calculate the average value of $T$ so obtained.

I did this quickly in Mathematica, obtaining $C$ as 60RandomReal[] . A quick run-through for $100000$ samples gave me expected values of $T$ consistently between $49.3$ and $49.4$ , where it belongs.

I think you are solving a different problem. You are choosing a sequence of items at different costs, and keep on doing so until the total cost exceeds $60$ . This sort of problem does give expected values involving $e$ , but this is not what is going on here.

Mark Hennings - 2 years, 9 months ago

@Mark Hennings – Thanks Mark for your answer. Now it's clear what the original problem dealt with. Actually, I did what you mention at the bottom. That was how I understood the original question. I did implement correctly the MC method, but not as you suggested, of course, but consistently with my interpretation of the problem. Indeed, we are solving two different problems. I encourage you to try and work out my problem too, since it appears to me to be much more involved to attack than the original one.

Stefano Micheletti - 2 years, 9 months ago

@Stefano Micheletti – If $X_1,X_2,...$ are independent $U(0,1)$ random variables, it is a simple induction that $P[X_1 + X_2 + \cdots + X_n \le x] \; = \; \frac{x^n}{n!} \hspace{2cm} 0 < x \le 1\;,\; n \in \mathbb{N}$ This probability is much more complex for $x > 1$ , but never mind. We deduce that part of the p.d.f. of $X_1+X_2+\cdots + X_n$ is equal to $f_{X_1+X_2+\cdots + X_n}(x) \; = \; \frac{x^{n-1}}{(n-1)!} \hspace{2cm} 0 < x \le 1 \;,\; n \in \mathbb{N}$ If $N$ is the number of $X_j$ required to add to more than $1$ , and $T$ is the largest running total of the $X_j$ that is less than $1$ , then $\begin{aligned} P[T \le x \,,\, N = n] & = \; P[X_1 + X_2 + \cdots + X_{n-1} \le x \,,\, X_1+X_2 + \cdots + X_n > 1] \\ & = \; \int_0^x f_{X_1+X_2+\cdots+X_{n-1}}(y) P[X_n > 1-y]\,dy \; = \; \int_0^x \frac{y^{n-2}}{(n-2)!} \,y\,dy \\ & = \; \frac{x^n}{n (n-2)!} \; = \; \frac{(n-1)x^n}{n!} \; = \; \frac{x^n}{(n-1)!} - \frac{x^n}{n!} \end{aligned}$ for $0 \le x \le 1$ and $n \ge 2$ and hence $P[T \le x] \; = \;\sum_{n \ge 2} P[T \le x \,,\, N = n] \; = \; x(e^x-1) - (e^x-1-x) \; = \; (x-1)e^x + 1 \hspace{2cm} 0 \le x \le 1$ Thus $T$ has p.d.f. $f_T(x) \; = \; \left\{ \begin{array}{lll} xe^x & \hspace{1cm} & 0 < x < 1 \\ 0 & & \mathrm{o.w.} \end{array} \right.$ and hence the expected value of $T$ is $E[T] \; = \; \int_0^1 x^2e^x\,dx \; = \; e - 2$ Which makes the answer to your question $60E[T] = 60(e-2)$ .

Mark Hennings - 2 years, 9 months ago

@Mark Hennings – Brilliant! I did it in a completely different way, but yours is theoretically neater and more elegant. By the way, how can you incorporate Latex commands in your posts, if this is the case?

Stefano Micheletti - 2 years, 9 months ago

@Stefano Micheletti – $\backslash\mathrm{alpha}$ works, but is a bit of a cheat (I am typing \backslash\mathrm{alpha} in a math environment).

In other implementations of LaTeX, the command \verb does the trick, but that does not seem to be implemented here.

Mark Hennings - 2 years, 9 months ago

@Mark Hennings – Thanks, I'll try!

Stefano Micheletti - 2 years, 9 months ago

@Stefano Micheletti – OK, so $ is the verbatim toggle here... Well, not quite, since $\backslash($ and $\backslash)$ commands are still active inside $.

Mark Hennings - 2 years, 9 months ago

Michael Mendrin
Aug 21, 2018

The expected value is that area of this square with the [infinite number of] triangles as marked subtracted from it, divided by the length of its side. The slope of the blue lines are $1, 2, 3, 4, 5,...$ . Any integer multiple of any value $x$ will be at the red bottoms of those triangles, if less the height of the square.

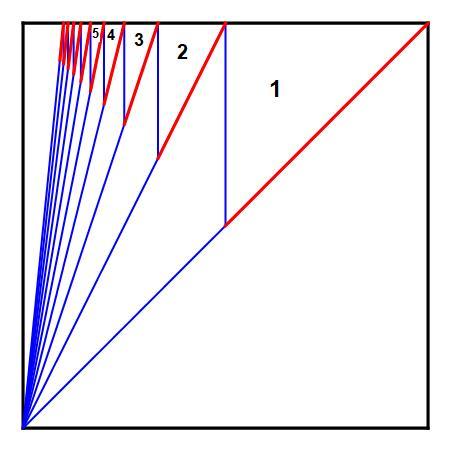
For an unit square, this area is

$1-\displaystyle \sum _{ n=1 }^{ \infty }{ \left( \frac { 1 }{ 2 } \dfrac { 1 }{ n+1 } \left( \frac { 1 }{ n } -\dfrac { 1 }{ n+1 } \right) \right) } =1-\dfrac { 1 }{ 2 } \displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { 1 }{ n{ \left( n+1 \right) }^{ 2 } } } =\dfrac { { \pi }^{ 2 } }{ 12 }$

To prove the above result, first we start with

$\displaystyle \sum _{ n=1 }^{ \infty }{ \left( \dfrac { 1 }{ n } -\dfrac { 1 }{ n+1 } \right) } =1= \displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { 1 }{ n\left( n+1 \right) } =\displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { n+1 }{ n{ \left( n+1 \right) }^{ 2 } } } } =\displaystyle \sum _{ n=1 }^{ \infty }{ \left( \dfrac { 1 }{ { \left( n+1 \right) }^{ 2 } } +\dfrac { 1 }{ n{ \left( n+1 \right) }^{ 2 } } \right) }$

Now, we know from the Basel Problem that

$\displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { 1 }{ { \left( n+1 \right) }^{ 2 } } } =-1+\dfrac { { \pi }^{ 2 } }{ 6 }$

so that

$\displaystyle \sum _{ n=1 }^{ \infty }{ \dfrac { 1 }{ { n\left( n+1 \right) }^{ 2 } } } =2-\dfrac { { \pi }^{ 2 } }{ 6 }$

Thus, the final expected value is $60 \cdot \dfrac { { \pi }^{ 2 } }{ 12 } = 5{ \pi }^2$

Alternative:

Let us denote amount of capital we have with $c$ , price of a random item with $p$ , number of items we can afford with $n$ and money we spent by buying $n$ items priced $\$p$ with $s = np$ . The following relationships hold when $n = k$ :

$\frac{c}{k+1}<p\leq\frac{c}{k}$
$\textrm{E}[s_{k}] = \frac{k(p_{max} + p_{min})}{2} = \frac{ck}{2}\left(\frac{1}{k} + \frac{1}{k+1}\right)$ (based on uniform probability distribution)
$\mathbb{P}(n = k) = \frac{1}{k} - \frac{1}{k+1}$

If we denote money spent with $S$ , we have:

$\begin{aligned} \textrm{E}\left [ S \right ] &= \sum_{k = 1}^{\infty}\textrm{E}\left [ s_{k} \right ]\cdot \mathbb{P}(n=k) \\ &= \sum_{k = 1}^{\infty}\frac{ck}{2}\left(\frac{1}{k} + \frac{1}{k+1}\right)\left(\frac{1}{k} - \frac{1}{k+1}\right) \\ &= \frac{c}{2}\sum_{k = 1}^{\infty}k\left(\frac{1}{k^{2}} - \frac{1}{(k+1)^{2}}\right) = \frac{c}{2}\sum_{k = 1}^{\infty}\frac{1}{k} - \frac{1}{k+1} + \frac{1}{(k+1)^{2}} \\ &= \frac{c}{2}\left(1 + \sum_{k = 2}^{\infty}\frac{1}{k} - \sum_{k = 2}^{\infty}\frac{1}{k} + \sum_{k = 1}^{\infty}\frac{1}{k^{2}} - 1\right) \\ &= \frac{c}{2}\sum_{k = 1}^{\infty}\frac{1}{k^{2}} = c \frac{\pi^{2}}{12}\end{aligned}$

By the way, I'm struggling to understand your square analogy. Could you explain it further?

Uros Stojkovic - 2 years, 9 months ago

Oh, I got it. It can be interpreted to be similar to my reasoning.

Uros Stojkovic - 2 years, 9 months ago

yeah, it started out by plotting how much money would be spent given the cost of any particular item.

Michael Mendrin - 2 years, 9 months ago

It is probably easiest to evaluate the sum as you had first written it and not rewriting as $\frac{1}{n(n+1)^2}$ . You can just distribute the $\frac{1}{n+1}$ to get $\frac{1}{n(n+1)}$ (a telesoping series) minus $\frac{1}{(n+1)^2}$ (a shifted basel problem).

John Ross - 2 years, 9 months ago

ahh maybe so, I could have gone that way

I actually first figured $\frac{1}{2} \frac{1}{n(n+1)^2}$ as the area of the triangles just from looking at the figure, and then decided to break it down for clarity later, on the left side.

Michael Mendrin - 2 years, 9 months ago

Do you think this problem is really similar with this one ?

X X - 2 years, 9 months ago

DEAR AUTHOR! please correct the text so the conditions of that "shopping" would be more clear! at this moment there are two ways of interpreting this puzzle's text and these two ways they lead to different solutions! (maybe not just two ways, maybe there's even more)

Nik Gibson - 2 years, 9 months ago

Uros Stojkovic
Aug 27, 2018

$\frac{c}{k+1}<p\leq\frac{c}{k}$
$\textrm{E}[s_{k}] = \frac{k(p_{max} + p_{min})}{2} = \frac{ck}{2}\left(\frac{1}{k} + \frac{1}{k+1}\right)$ (based on uniform probability distribution)
$\mathbb{P}(n = k) = \frac{1}{k} - \frac{1}{k+1}$

If we denote money spent with $S$ , we have:

Ervyn Manuyag
Aug 26, 2018

60/12xpixpi

Out shopping

4 solutions

0 pending reports