Outfoxing a Fox

Calculus Level 5

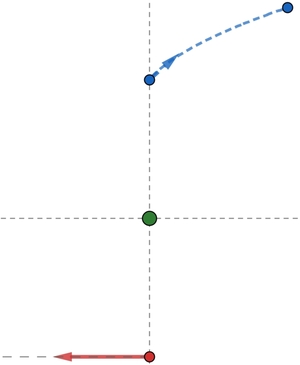
A rabbit is trying to avoid detection by a nearby fox.

Initially, the fox and the rabbit are out of each other's sights as they are on the vertical axis, and 1 unit away from a tree at the origin.

The fox starts to run to its left in a straight line with a constant speed 1 unit.

To avoid detection, the rabbit starts to run to its right along a certain path with a constant speed 2 units, so as to always keep the tree between itself and the fox.

Which of the given differential equations describes the path (in polar coordinates r = f ( θ ) r=f\left(\theta\right) ) of the hiding rabbit?

( d r d θ ) 2 = 4 cot ⁡ 4 θ − r 2 \left(\dfrac{dr}{d\theta}\right)^2=4\cot^4\theta-r^2 ( d r d θ ) 2 = 4 csc ⁡ 4 θ − r 2 \left(\dfrac{dr}{d\theta}\right)^2=4\csc^4\theta-r^2 ( d r d θ ) 2 = 4 tan ⁡ 4 θ − r 2 \left(\dfrac{dr}{d\theta}\right)^2=4\tan^4\theta-r^2 ( d r d θ ) 2 = 4 sec ⁡ 4 θ − r 2 \left(\dfrac{dr}{d\theta}\right)^2=4\sec^4\theta-r^2

Digvijay Singh by Digvijay Singh , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Steven Chase
Dec 5, 2018

Rabbit Position and Speed:

x = r c o s θ y = r s i n θ θ = a t a n ( 1 t ) v 2 = x ˙ 2 + y ˙ 2 = r 2 θ ˙ 2 + r ˙ 2 = 4 x = r \, cos \theta \\ y = r \, sin \theta \\ \theta = atan \Big(\frac{1}{t} \Big ) \\ v^2 = \dot{x}^2 + \dot{y}^2 = r^2 \dot{\theta}^2 + \dot{r}^2 = 4

Expanding and Applying Chain Rule:

r 2 θ ˙ 2 + r ˙ 2 = 4 r 2 ( d θ d t ) 2 + ( d r d t ) 2 = 4 r 2 ( d θ d t ) 2 + ( d r d θ d θ d t ) 2 = 4 ( d θ d t ) 2 [ r 2 + ( d r d θ ) 2 ] = 4 r^2 \dot{\theta}^2 + \dot{r}^2 = 4 \\ r^2 \Big ( \frac{d \theta}{dt} \Big)^2 + \Big ( \frac{d r}{dt} \Big)^2 = 4 \\ r^2 \Big ( \frac{d \theta}{dt} \Big)^2 + \Big ( \frac{d r}{d \theta} \frac{d \theta}{d t} \Big)^2 = 4 \\ \Big ( \frac{d \theta}{dt} \Big)^2 \Big [ r^2 + \Big ( \frac{d r}{d \theta} \Big)^2 \Big ] = 4

Calculating theta derivative:

d θ d t = d d t a t a n ( 1 t ) = 1 1 + 1 t 2 − 1 t 2 = − 1 1 + t 2 = − s i n 2 θ \frac{d \theta}{dt} = \frac{d}{dt} \, atan \Big (\frac{1}{t} \Big ) = \frac{1}{1 + \frac{1}{t^2}} \frac{-1}{t^2} = \frac{-1}{1 + t^2} = -sin^2 \theta

Plugging back in:

( d θ d t ) 2 [ r 2 + ( d r d θ ) 2 ] = 4 s i n 4 θ [ r 2 + ( d r d θ ) 2 ] = 4 ( d r d θ ) 2 = 4 c s c 4 θ − r 2 \Big ( \frac{d \theta}{dt} \Big)^2 \Big [ r^2 + \Big ( \frac{d r}{d \theta} \Big)^2 \Big ] = 4 \\ sin^4 \theta \Big [ r^2 + \Big ( \frac{d r}{d \theta} \Big)^2 \Big ] = 4 \\ \Big ( \frac{d r}{d \theta} \Big)^2 = 4 \, csc^4 \theta - r^2

9 Helpful 1 Interesting 0 Brilliant 0 Confused

Could you help me with something please? How can i find the distance traveled by the rabbit if it choses the hiding path that ends at the tree?

Digvijay Singh - 2 years, 6 months ago

Log in to reply

I used a numerical simulation to determine that the path is from ( r , θ ) = ( 1 , π / 2 ) (r,\theta) = (1,\pi/2) to ( r , θ ) ≈ ( 0 , 1.0894 ) (r,\theta) \approx (0,1.0894) . This website has a formula for polar arc length which plays very well with the result from this problem.

http://tutorial.math.lamar.edu/Classes/CalcII/PolarArcLength.aspx

Plugging in yields:

L ≈ ∫ 1.0894 π / 2 2 c s c 2 θ d θ ≈ 1.0447 L \approx \int_{1.0894}^{\pi/2} 2 \, csc^2 \theta \, d \theta \approx 1.0447

The path is almost a straight line from the start point to the origin, but it has a parabolic quality to it.

Steven Chase - 2 years, 6 months ago

Log in to reply

How did you find the lower limit of the integral? Does it have a closed form?

Digvijay Singh - 2 years, 6 months ago

Log in to reply

@Digvijay Singh – I don't know if it has a closed form or not, but here's how I found it:

θ 0 = π 2 r 0 = 1 Δ θ = − ϵ = very small negative number Δ r = 4 c s c 4 θ − r 2 Δ θ r k = r k − 1 + Δ r θ k = θ k − 1 + Δ θ \theta_0 = \frac{\pi}{2} \\ r_0 = 1 \\ \Delta \theta = -\epsilon = \text{very small negative number} \\ \Delta r = \sqrt{4 \, csc^4 \theta - r^2} \, \Delta \theta \\ r_k = r_{k-1} + \Delta r \\ \theta_k = \theta_{k-1} + \Delta \theta

Steven Chase - 2 years, 6 months ago

@Steven Chase @Digvijay Singh Can we solve the DE to get the exact function???

Aaghaz Mahajan - 2 years, 6 months ago

Log in to reply

No, we can't.

Digvijay Singh - 2 years, 6 months ago

You can see a detailed analysis of this problem in the book Chases and Escapes by Paul J. Nahin

Digvijay Singh - 2 years, 6 months ago

Log in to reply

Ok thanks!!!

Aaghaz Mahajan - 2 years, 6 months ago
Pedro Cardoso
Dec 6, 2018

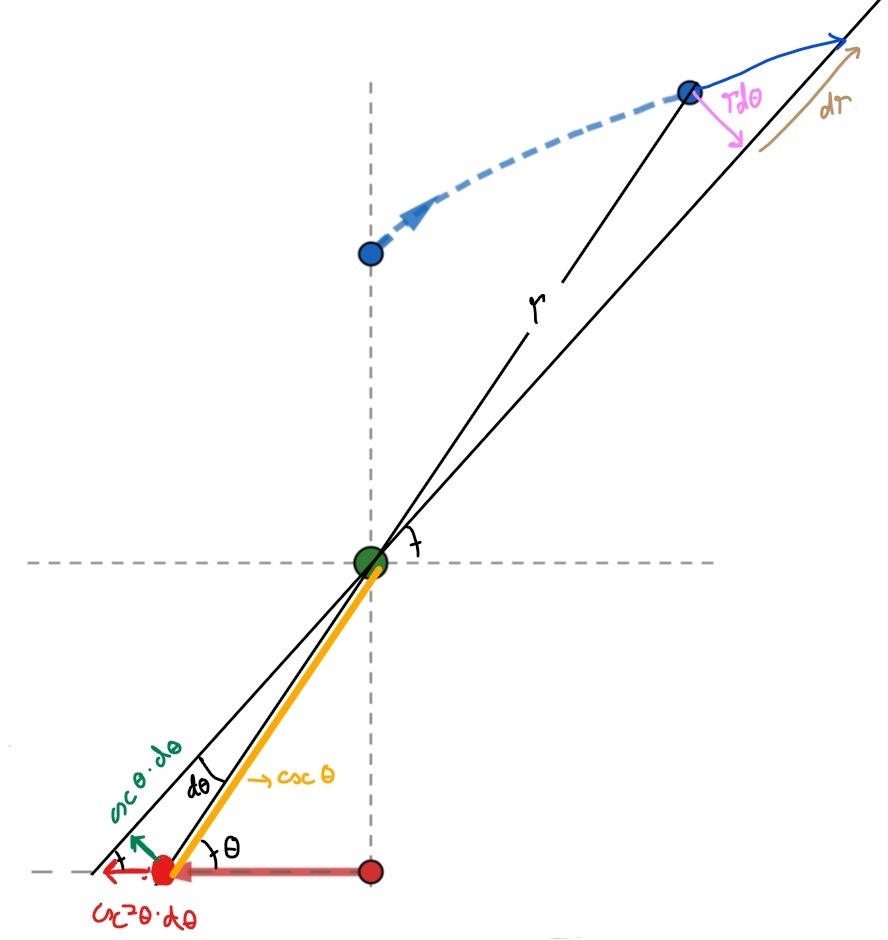
We'll split up the movement of the animals two: perpendicular to the position vector, and along the position vector. Let's consider what happens after the angle increases by an infinitesimal amount d θ d\theta (drawn big to make visualizing easier). Checking that all the lengths labeled are correct is preety straight forward from the triangles that form.

The size of the blue vector, that represents the change in the rabbit's position has to be twice the size of the red vector, that represents the change in the fox's position.

Thus, d r 2 + R 2 d θ 2 = 4 csc ⁡ 4 θ d θ 2 {dr}^2+R^2{d\theta}^2=4\csc^4 \theta {d\theta}^2

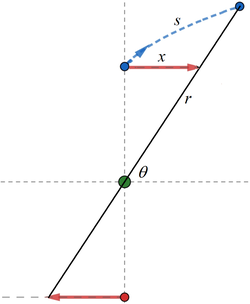
( d r d θ ) 2 = 4 csc ⁡ 4 θ − r 2 \left(\dfrac{dr}{d\theta}\right)^2=4\csc^4\theta - r^2

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Note that fox's path can be reflected to the positive side and let the length of the reflected path be x x . Let the length of the rabbit's path be s s . We note that x = t x=t , where t t denotes time. Therefore, cot ⁡ θ = x = t \cot \theta = x = t . Now consider the following:

r 2 ( d θ ) 2 + ( d r ) 2 = ( d s ) 2 Divide both sides by d θ r 2 + ( d r d θ ) 2 = ( d s d θ ) 2 = ( d s d t ⋅ d t d θ ) 2 Given that d s d t = 2 = ( 2 ⋅ ( − csc ⁡ 2 θ ) ) 2 Recall cot ⁡ θ = t ⟹ − csc ⁡ 2 θ d θ d t = 1 \begin{aligned} r^2 (d\theta)^2 + (dr)^2 & = (ds)^2 & \small \color{#3D99F6} \text{Divide both sides by }d\theta \\ r^2 + \left(\frac {dr}{d\theta}\right)^2 & = \left(\frac {ds}{d\theta}\right)^2 \\ & = \left({\color{#3D99F6}\frac {ds}{dt}} \cdot \color{#D61F06} \frac {dt}{d\theta}\right)^2 & \small \color{#3D99F6} \text{Given that }\frac {ds}{dt} = 2 \\ & = \left({\color{#3D99F6}2} \cdot \color{#D61F06}(-\csc^2 \theta) \right)^2 & \small \color{#D61F06} \text{Recall }\cot \theta = t \implies - \csc^2 \theta \frac {d\theta}{dt} = 1 \end{aligned}

⟹ ( d r d θ ) 2 = 4 csc ⁡ 4 θ − r 2 \implies \ \ \boxed{\left(\dfrac {dr}{d\theta}\right)^2 = 4\csc^4 \theta - r^2 }

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...