Oxford's Numerical Circle

Geometry Level 5

From ${\color{#333333}\text{BlackPen}}{\color{#D61F06}\text{RedPen}}$ 's video (see the section starting at 10:36), it can be shown that a circle has three points of tangency with the elliptic curve represented by the equation $y^2 - y = x^3 - x$ , where one exists at the point of symmetry.

Find the closed form of the radius $r$ and input $\lfloor 10^6 r \rfloor$ as your answer.

Fun Questions. Is there anything special about those points of tangency? If suppose we consider $y^2 = x^3 + ax + b$ , where $a$ and $b$ are some real values such that

$4a^3 + 27b^2 \neq 0$ ;
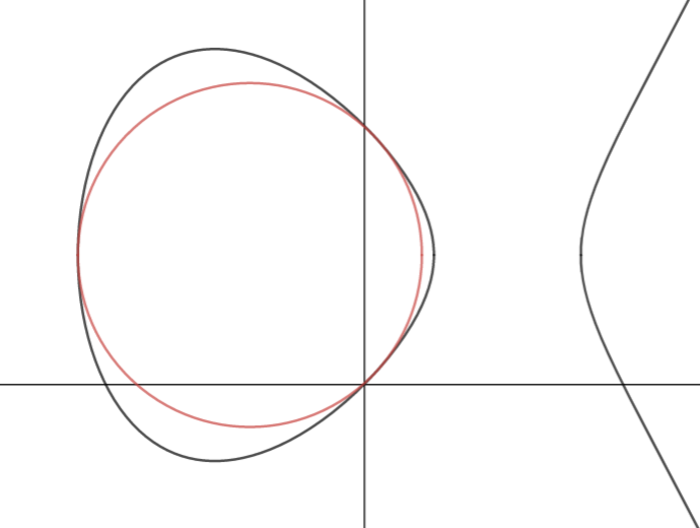
$a$ and $b$ altogether forms one closed loop as shown in the diagram;

What can be said about the area ratio of the maximized inscribed circle to the "loop"?

The answer is 665046.

1 solution

Chris Lewis
Mar 11, 2021

I've not seen the video yet so apologies if I'm going over old ground here.

First note the equation of the elliptic curve can be rewritten as $\left(y-\frac12\right)^2=x^3-x+\frac14$

so it is symmetric in the line $y=\frac12$ . Let the point of tangency with the circle on this line be at $P(u,\frac12)$ . Say the circle has radius $r$ ; its equation is then $(x-u-r)^2+\left(y-\frac12\right)^2=r^2$

We're interested in the intersections of the two curves. We know there's one at $P$ ; we want there to be exactly two others. By symmetry, these will both have the same $x$ coordinate, say $x=v$ .

We can eliminate $y$ by substituting in from the rewritten form of the elliptic curve into the equation of the circle; we get $(x-u-r)^2+x^3-x+\frac14=r^2$

Expanding and rearranging, this is $x^3+x^2-(2u+2r+1)x+\frac14+2ur+u^2=0$

Now, this has to have one root at $u$ and a double root at $v$ ; so we can write $x^3+x^2-(2u+2r+1)x+\frac14+2ur+u^2=(x-u)(x-v)^2$

Comparing coefficients, we get the following three equations: $\begin{aligned} 1 &= -u -2v \\ -(2 u + 2 r + 1)&=2 u v+v^2 \\ \frac14+2ur+u^2 &= -u v^2 \end{aligned}$

At this point, I used Wolfram|Alpha to solve these. Two sets of roots have $u>0$ (these correspond to the other vertical tangents to the elliptic curve), so we discard these. The other has a corresponding $r=\boxed{0.665046\ldots}$ .

NB: We could start by working out the value of $u$ , but as shown above we don't actually need to.

For completeness, $r$ is the positive root to the equation $32768 X^3 + 36864 X^2 - 13056 X - 17260 = 0$ , or $r = \dfrac1{16} \left(-6 + \dfrac{70 \cdot \sqrt[3]{4} }{B} + \dfrac{B}{\sqrt[3]{4}} \right)$

where $B = \sqrt[3]{2227 + 69 i \sqrt{111}}$ .

$r = \dfrac 3{32}\left[ \dfrac4{\sqrt3} \cos \left(\dfrac13 \tan^{-1} \sqrt{\dfrac{37}{27}} \right) + 2 \right]^2 - 1$

Pi Han Goh - 3 months ago

Nice - thank you for that!

Chris Lewis - 3 months ago

Hi @Pi Han Goh - resurrecting an old problem here. I've come back to this one (the bonus questions) and am finding something weird - I wondered if you had any thoughts on it, because I am completely stuck. I hope you don't mind having a look!

Specifically, I'm looking at the question of how big the circle can be inside the loop of a function $y^2=f(x)=x^3+ax+b$

For this to have a loop at all, $f(x)$ needs three real roots, say $u<w<v$ , so we can write $f(x)=(x-u)(x-v)(x-w)$ By Vieta, $u+v+w=0$ . By symmetry, the circle goes through $(u,0)$ and its centre lies on the $x$ -axis, so its equation is $(x-u-r)^2+y^2=r^2$

As before, if the circle is tangent to the loop at three points, there must be exactly three points of intersection between them; one at $x=u$ and two at some other $x$ value, say $x=t$ .

Substituting for $y^2$ , the intersection points satisfy $(x-u-r)^2+(x-u)(x-v)(x-w)=r^2$

Subtracting $r^2$ , $(x-u)^2-2r(x-u)+(x-u)(x-v)(x-w)=0$

so (as expected) we can divide through by $x-u$ to get $x-u-2r+(x-v)(x-w)=0$ whose discriminant should be zero (for the repeated root): $(1-v-w)^2-4(vw-u-2r)=0$

From this we get $r=\frac18 \left(-4 u - v^2 + 2 v w - w^2 + 2 v + 2 w - 1 \right)$

...which is great, except it doesn't work! At least, not always. I've made a simple GeoGebra page to show what I mean; you'll see that as you vary $v$ and $w$ , sometimes the circle fits the loop and sometimes it doesn't.

Any idea where I might have gone wrong in the logic above? I'm guessing I've made an assumption somewhere that isn't valid, but I can't see where. Thanks if you've read this far!

Chris Lewis - 1 month, 2 weeks ago

@Chris Lewis – Hi Chris, I just want to notify you that I'm aware of your message and I've been stuck on it for a couple of days now with no significant progress.

You might want to post this question on a note instead... And tag Mark Hennings...

Pi Han Goh - 1 month, 2 weeks ago

@Pi Han Goh – Hi, thanks for that! I'm glad in a way it's not something simple but it'd be good to get to the bottom of it. Let's see how we (or anyone else reading this section) get on and I'll work it up into a note if we get completely stuck.

Chris Lewis - 1 month, 2 weeks ago

@Chris Lewis – Update:

I'm wondering why you got to depress the cubic in the first place:

If you just start with a generic cubic function like $y^2 = (x-1)(x-2)(x-3)$ , then we can fit a circle that meets the two smaller roots in the circle-y loop:

$y^2 + (x - 3/2)^2 = 1/4$

So the figure only has 2 (not 3) intersection points with the circle-y loop.

Why I used a non-depressed cubic? Because all cubic polynomials can be depressed, so your graph of $y^2 = f(x) = x^3 + ax + b$ is simply my graph but the horizontal axis is shifted.

Pi Han Goh - 1 month, 2 weeks ago

@Pi Han Goh – Aha! I think you're onto something here. The depressed vs not depressed thing doesn't matter, as you say - it's just a horizontal translation (I only used that form because of the wording of the question).

BUT if the circle can meet the loop at the two axis intersections (and nowhere else), that will change things.

So now the question is, when is that possible? I hadn't actually noticed before, but if the loop exists, it's always going to be sandwiched between a pair of vertical asymptotes; if the function is $y^2=(x-u)(x-v)(x-w)$

with $u<v<w$ then $2yy'=(x-v)(x-w)+(x-w)(x-u)+(x-u)(x-v)$

If $y=0$ , then $x$ is one of $u,v,w$ ; but since these values are distinct, the RHS will be non-zero. But this can only happen if $y' \to \pm \infty$ , ie the tangent lines at $x=u,v,w$ are vertical.

I'm still a bit confused as to why the radius formula doesn't just give half the distance between the two roots in this case. But this feels like progress. I might try working through a case that seems not to work to find out exactly where it stops working, if I can.

Chris Lewis - 1 month, 2 weeks ago

@Chris Lewis – We can further assume that $u = 0$ because it's also shifting the horizontal axis only...

I will report back if I have anything substantive.

Pi Han Goh - 1 month, 2 weeks ago

Oxford's Numerical Circle

The answer is 665046.

1 solution

0 pending reports