Pac man cannibal

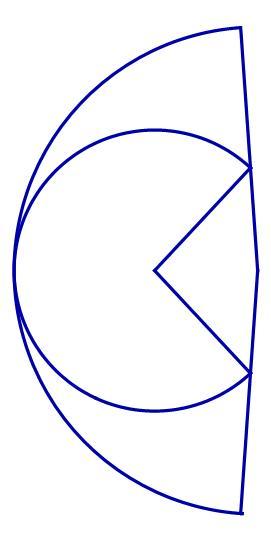
We see a yellow pac-man has eaten a smaller red pac-man. The angle formed by the yellow pac-man's mouth is twice as large as the angle formed by the red pac-man's mouth.
What is the angle of the red pac-man's mouth in degrees if the ratio Area red Area yellow is minimized?
Note: If the red one gets too big the yellow one might die.
The answer is 93.17991718.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
But here's the question. If pac-man opens his mouth greater than 180, is he still pac-man?
Log in to reply
Yeah, that's right... looks like what happens when a snake regurgitates
A good question, but still better than just calling them sectors, right?
Log in to reply
Jeremy, I think the problem would be clearer if you asked for the minimum ratio of yellow to red areas, i.e., A r e a r e d A r e a y e l l l o w , instead of "ratio of their two areas", which is a bit vague.
Yeah, it's just that I initially restricted my range of attention to (0,pi/2) in order to have a proper pac-man.
If the red pac-man has radius 1, and 2 θ is the angle of its mouth, then the yellow pac-man's radius is 2 cos θ + 1 1
The ratio of the areas simplifies to ( 2 cos θ + 1 1 ) 2 1 8 0 − θ 1 8 0 − 2 θ which is too messy to give an exact analytical solution.
Wolfram|Alpha says this is minimized if θ = 4 6 . 5 8 9 8 5 8 5 9 ∘ and so 2 θ = 9 3 . 1 7 9 9 1 7 1 8 ∘ and Geometer's sketchpad agrees.
A picture of this looks funny because the yellow pac-man's mouth is open more than 180 degrees.