Packing circles in a triangle
Three identical circles are cut out from a 30 ∘ -60 ∘ -90 ∘ right triangle with the second largest side length 141 centimeters.
To three decimal places, what is the largest possible radius of these circles in centimeters?
The answer is 18.235.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This is not really a proof. Why would the optimum solution necessarily have a circle stuck in each angular corner?
Log in to reply
The optimal solution isn't necessarily have a circle stuck in each angular corner, but in this case, it is. I believe that for other right triangle, it may not be. Hey, that's an idea for a new problem. Let me get on that one.
Log in to reply
For any triangle, the optimal solution must have, at least, 2 circles of the three stuck in the corners
Log in to reply
@Mr X – I said, "right triangle", but never mind that detail. I'm working on a version of this problem now.
I agree. I do not see why this must be the optimal solution.
As for the answer, it is not the original version of the question.
There is an admin who changed the text of the question.
The answer was 18235 corresponding to the floor of 1000 times the answer
⌊
1
0
0
0
A
⌋

L
e
t
r
=
t
h
e
r
e
q
u
i
r
e
d
r
a
d
i
u
s
.
T
h
e
t
o
p
⊙
b
e
O
1
,
m
i
d
d
l
e
,
O
2
,
b
o
t
t
o
m
O
3
.
T
h
e
1
4
1
v
e
r
t
i
c
a
l
l
e
g
A
B
a
n
d
h
o
r
i
z
o
n
t
a
l
l
e
g
B
C
.
O
1
O
2
∣
∣
A
B
c
u
t
B
C
a
t
M
.
O
3
N
⊥
B
C
,
N
o
n
B
C
.
S
t
.
l
i
n
e
O
2
O
3
C
a
n
g
l
e
b
i
s
e
c
t
o
r
o
f
∠
B
C
A
,
∠
B
C
O
2
=
3
0
o
.
A
O
1
a
n
g
l
e
b
i
s
e
c
t
o
r
o
f
∠
B
A
C
,
∠
O
1
A
B
=
1
5
o
.
O
1
T
=
r
⊥
A
B
,
T
o
n
A
B
.
O
3
C
=
r
/
S
i
n
3
0
=
2
r
.
∴
O
2
C
=
4
r
.
⟹
O
2
M
∣
∣
A
B
,
=
4
r
S
i
n
3
0
=
2
r
.
O
2
O
3
∣
∣
A
B
,
=
2
r
.
A
T
a
l
o
n
g
A
B
,
=
T
a
n
1
5
r
.
A
B
=
2
r
+
2
r
+
T
a
n
1
5
r
.
⟹
r
=
4
+
T
a
n
1
5
1
1
4
1
=
1
8
.
2
3
5
8
.
As mentioned by Mr. Michael Mendrin, in very details, out of the two best candidates, the middle one circle 2 with tangent to the long leg AB is the best solution since the triangle of centers O 1 O − 2 O 3 is the smallest, compact. The above solution is for that position. I first tried two circles 2 and 3 tangent to the short leg BC. The third was floating. Then thought of turning the two circles 2 and 3 about O 3 , so as to fill the vacant space, with third circle 1, tangent to the middle circle 2 as well as to AB and AC. I n t h e i s o s c e l e s Δ O 1 O 2 O 3 o f ⊙ s , O 3 i s o n a n g l e b i s e c t o r o f ∠ C , O 1 o n a n g l e b i s e c t o r o f ∠ A , O 1 O 2 = 2 ∗ r a n d ∣ ∣ A B . Then worked out a simple way to find r.
How do the solvers know in advance that O2O3C (in the lowest diagram) has to be a straight line? That certainly makes the solution easier to get. I did it without assuming that, by finding coordinates of O2 and O3 (using BC and BA as axes) in terms of the unknown radius r, then saying that the distance O2O3 has to be 2r, which made a quadratic equation in r that led to the same answer.
they have to be the same size and touching a side
This
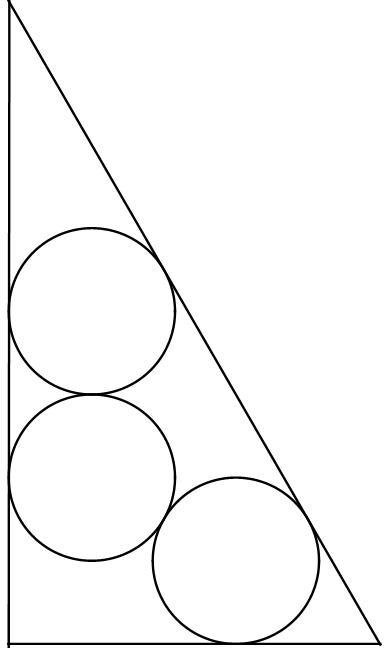
has a slightly better packing than
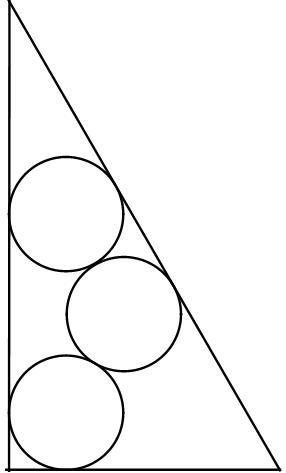
So how did you compute the answer of 18.235?
Log in to reply
Solve the following numerically:
( ( 1 4 1 − r cot ( 1 5 ) − 2 r ) − ( r ) ) 2 + ( ( r ) − ( 3 1 4 1 − r cot ( 3 0 ) ) ) 2 = 4 r 2
which is about finding the distance between the centers of the bottom 2 circles.
Log in to reply
How do you know that this is the optimal configuration?
Log in to reply
@Pi Han Goh – Any optimal configuration has to be "locked", i.e., none of the circles can move from its position. This means all three circles have to be tangent to 3 others things, either sides or circles. There's only so many ways to pack 3 circles like that inside the triangle, so it was a matter of picking out the most likely "best" candidates and comparing the two.
An example of "not locked" would be 2 circles touching the base of the triangle and the sides, while the 3rd is touching two sides at the upper part of the same. One of the 2 circles is still free to move, and certainly the 3rd one is free to move too. This allows an incremental increase in radius, and so is not even a local optimum.
Where could you practice this stuff?
Log in to reply
There are plenty of such amazing puzzles and problems on Brilliant!
The two isosceles triangle of centers are similar. But in seconds case the base is || to the longer side (hypotenuse) . In first case it is || to a short side (leg), so it is compact causing r to be bigger ?
You compared just two packings against each other.
Log in to reply
and a 3rd one would be?
Log in to reply
It's not up to me to give another one. The original poster needs to give an exhaustive proof of why he/she just presents those two.
My proof is pretty long, the main idea is that each of the circles centres has to be within a triangle similar to the original (as u draw parallels to the triangles sides at distance r). Then the tedious part is to prove that any triangle inscribed in the latter will have sa side no longer than r, which u find out as u prove.
For the optimum solution, one circle will be "stuck" in the 3 0 ∘ corner, and a second will be stuck in the 6 0 ∘ corner. These circles will be as large as possible to enable a third circle to be drawn.
If we are being picky, the answer is not correct in the third decimal place - to 3DP, the answer is 1 8 . 2 3 6 .