Pages

In the book, the numbers of each pages are placed in a specific way. If in a side of the sheet we have an odd number, the other side will have an even number in it. If each sheet is numbered in this way, we have a sheet with the numbers 1 and 2, a sheet with the numbers 25 and 26 and so on.

Then the sum of the two page numbers in a sheet will always be odd (even + odd = odd). We will sum up 25 sheets, or 25 odd numbers. How the sum of an odd number of odd number is always odd, after you sum up all of these numbers you will end up with an odd number as a result. How 1990 is even, then is impossible to obtain this sum.

I did this by asuming that we CAN get a sum of 1990 and seeing what page we would need to start on.

25 sheets is 50 pages. Let the first page ripped out be page "a", so the sum of the ripped-out page numbers is "a + a+1 + a+2 + ... + a+49". The sum 1+2+3+...+49 = 25*49 = 1225 (49th triangular number), and we have 50 lots of "a", so if we assume that the statemet is true we would get "1990 = 50a + 1225". Solving for "a", this would mean that the first page ripped out would have to be page 15.3, and you can't have .3 of a page, so therefore it is impossible.

In fact, if you started on page 15 and ripped out 25 sheets, the sum of the page numbers ripped out would be 50*15 + 1225 = 1975, so less than 1990. Starting on page 16 would be impossible because page 16 would be on the same sheet as page 15, and starting on page 17 would give a total sum of page numbers of 2075, which is bigger than 1990.

Let $S_b$ be the set of all sheets in a notebook with $b$ total sheets, and $x$ sheets ripped out.

$S_b= \{ a : 1\leq a\leq b \}$ where $a,\,b \in \mathbb{N}$ , and let $T_x\subset S_b : |T_x|=x$ where $x\in S_b$ .

Let $s_n$ be the set of page numbers on the $n$ th page of the notebook where $s_n = \{2n-1,2n\}$ and $n \in S_b$ .

$\sum s_n = 2n-1+2n = 4n-1$

Let $y$ be the sum of all the page numbers on the sheets in $T_x$ .

$y =\displaystyle \sum_{n\in T_x}\sum s_n \Rightarrow$

$y =\displaystyle \sum_{n\in T_x}(4n-1) \Rightarrow$

$y =\displaystyle \sum_{n\in T_x}4n - \sum_{n\in T_x}1 \Rightarrow$

$y = \displaystyle 4\sum_{n\in T_x}n - x \Rightarrow$

$x + y = \displaystyle 4\sum_{n\in T_x}n \Rightarrow$

$\displaystyle \frac{x+y}{4} = \sum_{n\in T_x}n$

Therefore, $\displaystyle n\in S_b \Rightarrow 1\leq n\leq b \Rightarrow n \in \mathbb{N} \Rightarrow \sum_{n\in T_x}n \in \mathbb{N} \Rightarrow \frac{x+y}{4} \in \mathbb{N}$ .

By the definition of divisibility, $\displaystyle \frac{x+y}{4} \in \mathbb{N} \Rightarrow 4|(x+y)$ .

Assume $V \in \{T_x\}$ and $V = \{n : n_m = m\}$ where $n_m$ is the $m$ th element of $V$ .

$\displaystyle \sum_{n \in V}(4n-1) = \sum_{m=1}^{x}(4n_m-1) = \sum_{m=1}^{x}(4m-1) = \sum_{m=1}^{x}4m - \sum_{m=1}^{x}1 = 4\sum_{m=1}^{x}m - x =$

$\displaystyle 4\bigg(\frac{x(x+1)}{2}\bigg) - x = 2(x)(x+1)-x = 2x^2+2x-x = 2x^2 +x$

Assume $W \in \{T_x\}$ and $W = \{n : n_m = b-(m-1)\}$ where $n_m$ is the $m$ th element of $W$ .

$\displaystyle \sum_{n \in W}(4n-1) = \sum_{m=1}^{x}(4n_m-1) = \sum_{m=1}^{x}(4(b-(m-1))-1) = \sum_{m=1}^{x}(4b-4m+4-1) = \sum_{m=1}^{x}4b - \sum_{m=1}^{x}4m + \sum_{m=1}^{x}3 =$

$4bx - (2x^2+2x) + 3x = 4bx - 2x^2 + x$

Since $V$ is the set of the first $x$ pages in the notebook and $W$ is the set of the last $x$ pages in the notebook, it is apparent that $(2x^2 + x) \leq y\leq (4bx-2x^2+x)$ .

Therefore, $\forall \: x \: \exists! \: Y_x = \{y : 4|(x+y) \land (2x^2 + x) \leq y\leq (4bx-2x^2+x)\}$ , where $x$ is the number of sheets ripped out of the notebook and $Y_x$ is the set of all possible sums of the page numbers on $x$ sheets.

---

Let $b=96$ , $x = 25$ , and $y = 1990$ .

$25\leq 96 \Rightarrow T_{25} \subset S_{96}$ , so this is a valid scenario. In order for $1990 \in Y_{25}$ , two conditions must be met:

• Condition 1: $4|(x+y)$

$25 + 1990 = 2015$ and $4\nmid 2015$

$\color{#D61F06}FAIL$

• Condition 2: $(2x^2 + x) \leq y\leq (4bx-2x^2+x)$

$2(25^2)+25 = 1275 \leq 1990 \leq 4(96)(25)-2(25^2)+25 = 8375$

$\color{#20A900}PASS$

Therefore, $1990 \notin Y_{25}$ .

---

In conclusion, it is impossible to rip out 25 sheets such that the sum of the page numbers on these sheets is exactly 1990.

Hence, the answer is NO .

---

Credit to Pranshu Gaba for noticing the need for an upper bound on $y$ .

Let the first page ripped out be x. Since the pages of the book must be consecutive, the next pages are x+1, x+2, and so on until x+24. The sum of these expressions is 25x added to the sum of the first 24 numbers. Gauss' formula tells us that the sum of the first 24 positive integers is 25*24/2 which is 300. This is 25x+300. This must be equal to 1990 because the question states that the sum is 1990. The equation is 25x +300 = 1990 which has no integer solutions so the answer is no.

No; To be $1990+25$ would have to be divisible by $4$ .

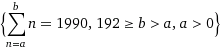
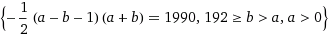
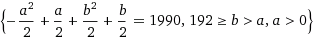
If we sum CONSECUTIVE page numbers from a to b (positive integers), with a>0 and 192>b>a (b can be the last page number), and force the sum to be 1990, the results for a and b must satisfy two conditions: a is odd and b is even. For languages writing from left to right, each sheet has an odd number on its left side and an even number on its right side in an ascending manner.

using WolframAlpha

Input: (sum(n), n=a to b)=1990, 192>=b>a, a>0

Result: Integer solution a=90, b=109 (both conditions are not satisfied), NOT POSSIBLE

Further, if we add a condition for b to be even in the WoframAlpha input, i.e., mod(b,2)=0, we get even values for b; but, values for a are not integers anymore.

This proof does not consider non-consecutive pages.

Just like (n+1) * n/2 represents the sum of the first n integers, you can write the sum of "n" consecutive integers (from x to x + n - 1) as (n/2) * (x + x + n - 1) = (n/2) * (2x + n - 1). In the case above, n = 50 (2 pages per sheet), so we have the sum as (50/2) * (2x + 49) = 50x + 25*49. Setting this equal to 1990, we have 50x + 1225 = 1990, which results in a non-integer solution for x (15.3). Therefore there is no solution that satisfies this question.

no because 1990 is not divisible by 25.

The sum of these page numbers is really higher than 1990, so even if we rip the 25th highest pages the sum we'll get will be above 10000.