Go g r e e n !
You paint the 5 × 5 grid green, one square at a time. You can only paint a square green if it shares an edge with 1 or 3 yellow squares (diagonals don't count).
What's the maximum number of squares you can color?
Below right is an example of a sequence of how you might paint the first 3 squares.
Clarification:
The square colored green with sequence number 2 now borders two yellow squares, but it was bordering three yellow squares at the time of coloring.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Here is another solution to the 7 x 7 square:
 7 x 7 square
7 x 7 square
Log in to reply
That's a nice approach! I didn't think of that! 👍
There are many ways to do this. My strategy is to build a set of "skyscrapers" up from the bottom in columns 2, 4, 6, ... each going up to all but the top row. Then fill the gaps between the "buildings" from bottom to top. That leaves the top row which you can fill from either side until there's one empty square left. I also like your inductive proofs.
Log in to reply
Yep there is. And thank you!
My initial approach was the same, but when looking at H.M.'s propose to find a way to generalize it, I realized that approach doesn't work with n x n square when n is even. Just have to bend the "skyscrapers" sideway.
There is a small problem with this as a proof which is probably been left as it is trivial: We have not shown that it cannot be done with 25 squares being coloured green. However, when there is one square left it cannot be adjacent to a yellow square (because all the rest are green) so cannot have one or three sides in contact so cannot be coloured green. I know this is just picky, but it is the cherry on top of the icing on top of the cake.
Log in to reply
Let me copy paste what I said: "We know that whatever we try, the last square can't be filled."
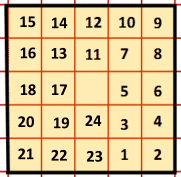
Whatever you may try, you'll always get number of green as multiple of 4, or there is some more green box left. So highest multiple of 4, that is smaller than 25 is 24.
Here is a solution for 24:

And, clearly you can't do it in more that 24, since it would be impossible for the last square to have an odd number of yellows next to it.
Based on your solution, we can always reduce n x n square to (n - 2) x (n -2) square, until n <= 2:
 n x n square
n x n square
-
When the inner square is 2 x 2:

So when n is odd, all can be filled but 1. When n is even and > 2, all can be filled but 2.
Log in to reply
Nice writeup, Kyle! But how can we show that we can never do better than "all but 2" for even n I wonder?
So, for n × n it will be n 2 − 1
Log in to reply
Not for all n ... For example, for n = 2 , it will be zero.
Log in to reply
For n>=3 ???
Log in to reply
@Kushal Bose – Interesting hypothesis... I'm not sure... Can it be done for n = 4 ?
Log in to reply
@Geoff Pilling – I am getting 12
Log in to reply
@Kushal Bose – Looks like n = 4 is a much more interesting question! Lemme see if I can beat 1 2 ...
Log in to reply
@Geoff Pilling – Divide the concept for even and odd. n.For odd n >=5 I am almost sure it will be n^2-1.For even i need to think
Log in to reply
@Kushal Bose – Yes... I agree with you, Kushal... For odd n , I think your answer works (even for m × n where one of either m or n is odd)... All but one square. I'm also not sure about even n . But now you've got me curious... Lemme see...
Log in to reply
@Geoff Pilling – I believe for even n ( > 3 ) the answer is all but 2 ... But how to prove it... Hmm...
Log in to reply
@Geoff Pilling – It's not too hard to reduce any n x n square to a (n-2) x (n-2) square (with n>2).
So n=6 reduces to the 4 x 4 case, and we know we can do all but 2, etc.
You can reduce the 4 x 4 case to a 2 x 2, but that is not optimal.
Log in to reply
@Steven Perkins – Good observation, @Steven Perkins !
So, I am guessing that the answer is "all but 2" for even n (except n=2), and "all but 1" for odd n, but I still haven't been able to prove that we can't do better for even n... Although the more I look at it, the more I convince myself that we can't...
Log in to reply
@Geoff Pilling – Assuming that "all but 2" is true for even n, where n>2, we could reduce it to a single statement which encompasses both odd and even n.
( n 2 − 1 − ( n + 1 ( m o d 2 ) ) ) ∧ ( n > 2 )
@Geoff Pilling – Yes, we haven't proven that "all but 2" is optimal for all even squares. Or for all even rectangles. Just that we can do at least that good.
Indications are that is the best we can do, but how to prove it is an interesting question.
@Geoff Pilling – need time to think
@Kushal Bose – I can get 14 as follows:
| 5 | 6 | 1 | X |
| 4 | 7 | 2 | 12 |
| 14 | 13 | 3 | 11 |
| X | 8 | 9 | 10 |
Is it possible to get 15?
Log in to reply
How did you find this sequence? Is there a way we can employ an algorithm to solve this problem for an arbitrarily large square?
https://goo.gl/photos/jvfjfs8FmCdUqxGk9
I actually put 25, because I forgot about the last square. :)
I knew the answer was 24 because I played a handled puzzle game called "lights out" as a kid. It had the same rules as applied here, except every square you hit that wasn't lit would light up, and every square you hit that was lit would go dark. In addition, every square that shared an edge with the square that you hit would invert its state (again, diagonals don't count). Thus if the square above the one you touched was off, it would turn on and vice versa.
There were hundreds of pre-progrmmaed starting configurations, the goal being to get all the lights out, then there was a mode that you could set the starting lights yourself and try to solve. After many tries I realized it was impossible to begin with every square lit and get them all to go out. There would always be one...
I'd like to see an algorithm that can accomplish this in plug & play fashion. I suspect the developers knew one, as there were so many pre-programmed puzzles.
There's a solution for this, yes, we're clear, right?
Then let's generalize it.
For an odd number n ≥ 5 , make an n × n square. I'll show you an example of n = 7 .
Look at the block in the down-left corner. Now you'll see that you can paint the block to the right side of that block. Paint it.
Then, paint the down-left corner. After that, imagine there's a block below the down-left corner. Look at it and repeat the procedure below.
Go up by 3 blocks and make sure it isn't another corner block. If it is, end the procedure.
Paint it.
Go down by 1 block and paint it.
Below is the result of the example grid.
Now at the end of the procedure, you're 3 blocks down from the up-right corner block. Paint the block to the right side of that block.
Then, paint the up-left corner. After that, paint the block that's one block down from the block you just painted.
Look at the up-left corner block and repeat the procedure below.
Go right by 3 blocks and make sure the block exists. If it doesn't, end the procedure.
Paint it.
Go left by 1 block.
Below is the result of the example grid.
By the end of the procedure, you know how to paint the rest of the perimeter of the grid.
And you'll see that you can fill up the grid's perimeter completely.
Below is the result of the example grid.
You see that the grid has gotten smaller into ( n − 2 ) × ( n − 2 ) grid?
Now all we need to see is how 3 × 3 grid gets filled.
And the result is as you see below.
We know that whatever we try, the last square can't be filled.
Therefore, for an odd number n , the grid can always be filled with n 2 − 1 green squares.
And for this question, n = 5 . Therefore, the grid can be filled with 2 4 green squares.