Painting a 2x2x2 Cube

Probability Level 1

Suppose you have a $2 \times 2 \times 2$ cube and you can color each of the 24 little squares one of $\color{#D61F06}\text{f}\color{#20A900} \text{o}\color{#3D99F6} \text{u}\color{#EC7300} \text{r}$ colors.

Is it possible to paint the cube so that the following holds true?

None of the 3 squares meeting at a corner are the same color.
None of the 4 squares meeting along an edge are the same color.
None of the 4 squares on any face are the same color.

Yes No

13 solutions

Marcel Sévigny
Mar 12, 2018

Here is an example of the pattern for the cube in question. Each apex is identified by a number making it easier to verify that different colors are related.

good solution

Mohan Kollu - 3 years, 3 months ago

There are 2 greens along 3-6.

Rodrigo Romea - 3 years, 3 months ago

and two pink squares along 4-8

Pepe Berges - 3 years, 3 months ago

Big thanks to both of you, I fix the little mistake! You were right, and now everything is perfect (I hope...)

Marcel Sévigny - 3 years, 3 months ago

Is it just me, or is there a big black rectangle covering the lower half of this image?

Geoff Pilling - 3 years, 2 months ago

I don't have that rectangle on my display. Have you reloaded the page ?

Monty McGee - 3 years, 2 months ago

Seems to look fine now... Not sure what happened.

Geoff Pilling - 3 years, 2 months ago

Geoff Pilling
Feb 28, 2018

The following is one solution:

		2	1
		3	4
1	4	1	2	3	2
3	2	3	4	1	4
		1	2
		4	3
		2	1
		4	3

Where 1, 2, 3, and 4 represent different colors, and you fold it up into the 2x2x2.

Moderator note:

There are only two solutions (ignoring the fact numbers can be swapped since they arbitrarily indicate colors anyway).

Without loss of generality, let the "center" face of the diagram be as shown:

Using the property of adjacent edges having all four colors different and all faces having all four colors different, we can fill in "forced pairs" on the entire grid. For example, above the center square the digits must be 3 and 4 in some order, since they are on the same edge as a 1 and 2.

(The notation has the numbers written between the spaces they can be entered into.)

Now, if we enter one of the digits (say, the "3" above the "1") this forces a chain of logic. For example, the digit to the right must be a 4; this forces the "2 4" pair on the right side to have the 4 on bottom (because it will otherwise meet the 4 that just got added) which forces a 2 on top.

Using the same steps throughout this ends up creating a chain which fills the entire grid; in the case, the exact one given in Geoff's answer.

If we trace all the way back to the when we guessed "3" above "1" and put the other option instead ("4") we get yet another logical forced chain that fills in the entire grid:

Can you elaborate on what the whole diagram means? You say to fold it into 2x2x2, but in which way? They're all in a single column, and you can't make a cube out of a single column (or at least I can't.).

Ryan Huynh - 3 years, 3 months ago

if we fold and look at it this way, without turning it:

2 1 3 4 is the top side

1 4 3 2 is the left side

1 2 3 4 is the side we see head on

3 2 1 4 is the right side

1 2 4 3 is the bottom side

2 1 4 3 is the side we can’t see

Ria Gray - 3 years, 3 months ago

Is this problem related to the four colour map theorem?

John Frank - 3 years, 3 months ago

Instead of colors, numbers were used. It’s the same problem, but with numbers instead of colors.

Ria Gray - 3 years, 3 months ago

No it is not, because the four color theorem only holds for planar graphs, and since the K3,3 minor graph is included in the cube graph, it cannot be planar. Interestingly enough, this is a typical application field of contraint satisfaction methods like backtracking and constraint propagation.

Michael B - 3 years, 2 months ago

Can anyone tell the solution using graphs?

Rishabh Gupta - 3 years, 3 months ago

you don't untouched IT

许宏量 - 3 years, 3 months ago

Great explanation, but I think there is a typo in the top four squares of the last image, since it still has a 3 above the 1, and this is not a solution, since, for example, the 3 at the top shares an edge with the 3 on the left.

Geoff Pilling - 3 years, 2 months ago

Yes, one of the pairs was left unswapped. I fixed it, thanks.

Jason Dyer Staff - 3 years, 2 months ago

Actually it's not necessary that each square on each face is unique. It's said in the description that none of the 4 are the same, but two or even three of them can be the same. So that your statement "without loss of generality" doesn't holds, because you assume that those first 4 squares are pairwise distinct. And this solution is not the only one, because there are combinations where there are two squares on the same face that have the same color

Alex Z - 3 years, 2 months ago

When it says that none of the four of them are the same, it is not saying that "They are not all the same", it is saying that no two of the four are the same, in which case the "without loss of generality" statement does indeed hold. Anyway, I can understand the confusion, so I'll think about how I can update the verbiage.

Geoff Pilling - 3 years, 2 months ago

I used the exact same method! The only difference was that I used "abcd" and not "1234".

Simon The Great - 3 years, 2 months ago

Pj Van Camp
Mar 12, 2018

This is an application of the four color theorem

"In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet." Wikipedia

Moderator note:

As pointed out in the comments, the 4-color theorem holds for planar graphs . Unfortunately, the graph of the cube cannot be represented as a planar graph.

The four color theorem does not directly apply as the graph you would have to color here would not be planar. You need to do a bit more to solve this.

Jake Retallick - 3 years, 3 months ago

Yes, it does apply in this case. The four color theorem for planar graphs can be stated as (quoting Wikipedia) «the vertices of every planar graph can be colored with at most four colors so that no two adjacent vertices receive the same color, or for short, "every planar graph is four-colorable"» https://en.wikipedia.org/wiki/Four color theorem. A cube can be represented as a planar graph (https://www.quora.com/Is-a-cube-a-planar-graph). Subdividing each face into four pieces is just taking each existing vertex and replacing it with four new vertices. The resulting graph is still planar.

Marcelo Magallon - 3 years, 3 months ago

Yes a cube can be made into a planar graph but that does not extend to our problem here: Each square becomes a vertex in our graph: v = 24 total vertices. Each face of the cube must contain all four colours: 6 edges per face * 6 faces = 36. Each edge of the cube must contain all four colours: 4 edges (6 but 2 already contained in the faces) per edge * 12 edges = 48. In total, we have v=24 vertices and e=84 edges in our "graph". A planar graph must satisfy e <= 3v-6: i.e. 84 < 66 which is a contradiction. Hence the graph for this problem is non-planar.

Jake Retallick - 3 years, 3 months ago

@Jake Retallick – Right, also you can find the K3,3 minor graph in 4 adjacent faces which form a 'loop'.

Michael B - 3 years, 3 months ago

@Jake Retallick – Where did you get 84 from? A sentence ago you had said 48, which agrees with my calculation.

Stewart Gordon - 3 years, 2 months ago

The four color theorem doesn’t apply because there are squares that do not share an edge but must still be different colors. Eg the four squares on one face.

Jeremy Galvagni - 3 years, 3 months ago

Those squares share an edge, the edge is just not the edge of the full cube. Understanding is easier if you separate the edges of the geometric object from the "borders" of the "countries" (in the same way that there's no physical discontinuity between neighboring countries on a map).

Trebor Shankle - 3 years, 2 months ago

You say "the edge is just not the edge of the full cube", but what exactly are you using "edge" to mean? If you mean one of the line segments separating regions of different colour, then there is no such line segment separating regions that are diagonally opposite on the same face of the cube. There is only a single point.

Stewart Gordon - 3 years, 2 months ago

You could use the four color theorem if you have some imagination and map this problem into a planar graph coloring problem though. Here's how you do it: 1) Turn the cube into the shape of a shere 2) Make the middle of the faces the vertexes of the graph 3) Whenever the faces of the cube touch, put an edge in the new graph 4) Take the stereographic projection of the graph to map a sphere into a plane 5) Notice you're trying to 4 color a planar graph 6) QED

Michael Tardibuono - 3 years, 2 months ago

That won't work at the step of projection. There will always be a side that should be connected to another side, but isn't on a 2d graph, and so it won't be a true planar graph, but simply a representation of a graph in 3D that doesn't have the true characteristics of a 2d graph. Clearly a sterographic projection isn't a planar graph in the strictest sense, which is the meaning the four color theorem uses: https://en.m.wikipedia.org/wiki/Stereographic_projection

David Weisberg - 3 years, 2 months ago

"There will always be a side that should be connected to another side, but isn't on a 2d graph" - how do you mean?

Stewart Gordon - 3 years, 2 months ago

I'm confused about why people think the graph isn't planar. Any polyhedron of genus 0 can be punctured (through a face, not an edge or vertex) and stretched flat (a stereographic projection is just one geometric transformation equating to this), thereby producing a planar graph. I'll try to produce an image when I've a bit more time.

Of course, this doesn't change the fact that the four-colour theorem isn't useful to us because we require for this problem that no two faces sharing a vertex be of the same colour.

Stewart Gordon - 3 years, 2 months ago

I've just realised. What is relevant is the graph representing what is considered adjacent for the purposes of this problem - so each cell would be represented by a node, and each adjacency via either edge or corner would be an edge in the graph. So you're saying this graph isn't planar?

Stewart Gordon - 3 years, 2 months ago

I guess some guy proved that theorem wrong using some 1581 or something roughly that large number of figures

Aatman Supkar - 3 years ago

Munender Singh
Mar 12, 2018

My solution is a bit different . It requires logic & imagination. The first condition is true already(as none of the corner pieces match) in the original cube so we will not tamper with any of the corner pieces. Now for the edge pieces. You simply invert (Flip) the colours on any edge. For example , on the first edge you change blue with yellow ,on the second one you let them as they are and so on but remember to leave the corner pieces intact. Now to fulfill the last condition you take the colours on the corners and flip them with the colour on top This will ensure that all the colours are different and all the conditions are met. (Q.E.D

or else you can make a face with all 4 colours and make the cube on the basis of it.

PS - I am new on brilliant so if there is anything wrong with this logic please let me know in the comments.

Nothing is wrong with your logic. But plz next time, whether you mind or not, put commas and punctuations so that your statements will be easier to comprehend. I ran out of breath reading your solution.

Victor NG - 3 years, 3 months ago

The logic is fine, the punctuation is not as good. There was no punctuation at all in the whole solution, nor were there any capital letters.

Sophia Cai - 3 years, 2 months ago

I am tremendously sorry. As I was in a bit of a hurry while writing the solution , I didn't write it with great care and the answer turned out to be a bit too sloppy.

munender singh - 3 years, 2 months ago

Laura Gao
Mar 12, 2018

Relevant wiki: Four Color Theorem

This is basically the four color theorem.

On any surface with no "holes" in it (genus 0) divided into sections, it is always possible to have no two bordering sections share the same color with only $4$ colors.

Alain Zhang
Mar 14, 2018

In order to paint the cube described in the problem, each side must be distinct from another meaning that the pattern of squares cannot be rotations of each other. Knowing this, there are 4! = 24 possibilities to create one side of the cube. However, since each possible side can be rotated four times without changing the pattern of the squares, we must divide by 4 to get 6 ways to create one side of the cube which therefore means that such a 2x2x2 cube can be painted using four colors.

I like the elegance of this. Is there an intuitive reason why each side cannot be a rotation of the others? Beyond proof by contradiction considering adjacent and opposite sides. And is this condition equivalent to the description in the problem or merely a consequence of it? Thanks.

Daniel Singarajah - 3 years, 2 months ago

Eleanor Wroblewski
Mar 17, 2018

I worked out this problem by using colored sticky notes on my 2x2 rubiks cube. If anyone is having difficulty with the 2d representations I highly recommend this solution!

Pyrrhos Stathis
Mar 17, 2018

Redraw the shape into an equivalent planar shape

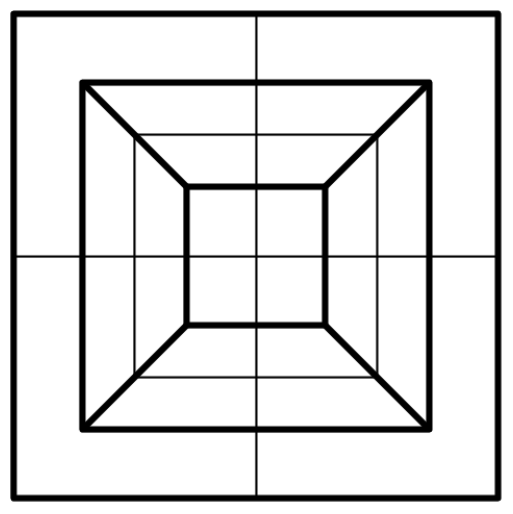
and apply the "four color theorem" which states that no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. https://en.wikipedia.org/wiki/Four color theorem

Ah... Great observation, Pyrrhos!

Geoff Pilling - 3 years, 2 months ago

Actually, come to think of it, the map you drew appears to be almost correct. In fact the regions in the far opposite corners are also not allowed to be the same color.

Geoff Pilling - 3 years, 2 months ago

The far opposite corners could be redrawn to touch by wrapping them around. However as @Michael B noted the diagonal squares on the faces (and the edges) do not border (and cannot be redrawn to do so) so my solution is indeed wrong. Thanks for the feedback.

Pyrrhos Stathis - 3 years, 2 months ago

Can you explain how your projections works? Otherwise, I'm pretty sure your solution is wrong.

Michael B - 3 years, 2 months ago

The thick lines represent the edges of the cube. The cube is stretched open in all directions, so to speak, from the middle of the back face of the cube. The diagonal squares on one face do not share a border so I believe this planar shape is border-wise equivalent to the un-stretched cube.

Pyrrhos Stathis - 3 years, 2 months ago

As @Geoff Pilling pointed out, your shape does not respect the last invariant. In your shape it is possible to fill diagonal squares on the same face with same color, because they dont share a border. If you would convert this into a graph with nodes and edges, the face invariant combined with the loop properties of a cube would result in a minor K3,3 graph indicating that the graph is not planar.

Michael B - 3 years, 2 months ago

@Michael B – You are right! Come to think of it, it also doesn't satisfy the second condition, since the four colours along the edge are in the same arrangement as the faces, the diagonals do not touch. Thanks for the feedback.

Pyrrhos Stathis - 3 years, 2 months ago

Momentimum .
Mar 16, 2018

This is what I thought of. Two of the options are possible.

This doesn't appear to fit the criteria.

Geoff Pilling - 3 years, 2 months ago

Sophia Cai
Mar 16, 2018

I have a super easy solution that requires almost no thinking at all. Imagine a sphere split into 24 parts in the same way as the cube. According to the four-color theorem, they can be colored with 4 colors only. Therefore, it's possible. Comment if you find a problem, because I have a feeling this shouldn't be so easy.

I take back one of my original comments, and rephrase... The four color theorem does indeed hold for 2D objects, and some 3D objects including spheres. However, it doesn't apply here, as four colors meeting on an edge or vertex is a different criteria than that set up by the four color theorem, since it allows for colors to meet at a vertex, but this problem does not.

Geoff Pilling - 3 years, 2 months ago

Book Armaments
Mar 13, 2018

Here is one solution.

Dorothy Taylor
Mar 13, 2018

I used the four-colour theorem.

Jam M
Mar 12, 2018

If the four different colors are Red (R), blue (B), yellow (Y), and green (G), then the following coloring of the 2x2x2 cube satisfies the given conditions:

                                                          Y  R
                                                          B  G
                                                    G  R  Y  R  Y  B  G  B
                                                    Y  B  G  B  G  R  Y  R
                                                          R  Y
                                                          G  B

Painting a 2x2x2 Cube

13 solutions

Moderator note:

Moderator note:

0 pending reports