Painting Squares

How many ways are there to paint a 3 × 3 grid with three colors such that each row and column has all three distinct colors?
Note: If you rotate the above illustration by 9 0 ∘ , 1 8 0 ∘ or 2 7 0 ∘ , they each count as different ways to paint the 3 × 3 .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
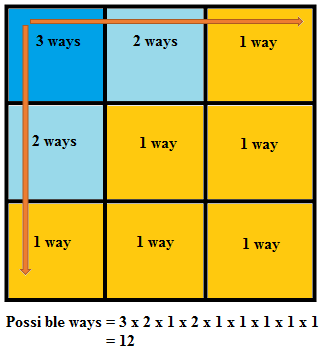
It's quite easy actually. We can first keep the rows the same (assume them as rigid boxes) and arrange them vertically. This can be done in 3! ways, each time generating a unique solution. Similarly we can do the same for the columns. 3! + 3! = 12.
Log in to reply
a) Rearranging the three rows gives 3! solutions, true. But how do we know that rearranging the columns would generate solutions which are all different from the 'rearranged rows' solutions?
b) In fact, the 3! 'rearranged rows' solutions and the 3! 'rearranged columns' solutions do have at least one solution in common - the 'starting' solution as illustrated. RGB / BRG / GBR
c) A little experimentation revealed two more overlapping solution: BRG / GBR / RGB and GBR / RGB / BRG
d) Further investigation reveals the three solutions which cannot be generated by rearranging the rows or columns: RBG / GRB / BGR and BGR / RBG / GRB and GRB / BGR / RBG
Postscript to my other reply: The three solutions which are not generated by rearranging rows or columns represent keeping one colour the same (e.g the red diagonal) and swapping the other two (e.g. green and blue). It is clear that the only rearrangement which keeps the red diagonal in place (i.e. doing nothing) also keeps the other two colours in place.
this is not correct.....this solution adds to 13 not 12
Log in to reply
you need to multiply the possible ways (combinatorics: rule of product)
For each colour that occupies the diagonal line of a 3x3 grid, there are 4 unique configurations, all of which can be achieved by rotating the grid through consecutive 90 degrees turns.
Once a full rotation has been completed, switch the colour and repeat until all 3 colours have occupied the diagonal line and completed full rotations.
3 × 4 = 1 2

It's not as mathematically pleasing (or adaptable to larger grids), but still solves this particular problem.
But visually very pleasing! :-) What a great write up! (Wish I could upvote it more than once!)
Log in to reply
Thanks! You're very kind.
Admittedly, it took me quite a while to make that GIF. I originally tried compiling them into a single grid that changed colour, with many more separate compositional images, but it had technical issues.
I automatically excluded rotations as they to me are individual solutions.
Log in to reply
Interesting perspective. Did you submit an answer of 3?
Ah, I've added the clarification.
Why is it necessary for a colour to occupy a diagonal?
Log in to reply
Whichever color occupies the central square must also be on opposite corners, forming a diagonal line.
Log in to reply
@Satvik Golechha – Indeed. If we start creating a configuration by filling the centre square, the adjacent squares cannot be used by the same colour, which leaves only the corners available. Once one of the corners is filled, the other corners in the same column and row cannot be used either, which leaves the opposite corner - forming a diagonal line. And this only requires one colour to be present.
 Invalid squares become greyed out as colours are filled.
Invalid squares become greyed out as colours are filled.
Now that we know that it's impossible to not have a diagonal line in a 3x3 grid, we can determine the remaining squares must also form a set pattern.

The problem then becomes a case of swapping the central colour and orientation, as the other two colours switch positions via rotation.
I could just have easily stated only the central square in the opening sentence of my solution, but my mind latched onto the observable diagonal line.
Log in to reply
@Jonathan Quarrie – Well said... And, nice animation! :-)
If we number the squares as follows:

There are six ways to paint 1 and 2.
Then, given 1 and 2, there are two ways to paint 4.
After that, there is only one way to paint the remaining boxes.
Therefore, there are 6 ⋅ 2 = 1 2 ways to paint the squares.
I think you have to prove that each of the 12 ways is consistent. For example, when you get to square nine, it has to satisfy two constraints. Are you assuming that for each of the 12 previous choices, there is a color that satisfies both constraints? Or is this obvious in some way that I am missing?
Log in to reply
That's what is intended in "After that, there is only one way to paint the remaining boxes.". If it didn't satisfy both constraints, then there would be "no way to paint the remaining boxes".
The explanation step that is skipped is:
1) Ensuring that there is at most one way which works,
2) Ensuring that each of the choices leads to one way.
i don't get
A bit more "why" in an explanation would be useful.
I suspect that the number of colorings for an n by n square is k = 1 ∏ n k ! .
Log in to reply
Ah, ok, so let's see what this gives for a 4x4...
1 ! ⋅ 2 ! ⋅ 3 ! ⋅ 4 ! = 1 ⋅ 2 ⋅ 6 ⋅ 2 4 = 2 8 8
Hmmm... Somehow I got 576. Lemme check my work...
Log in to reply
Ah, I think that you're right! These are known as Latin squares , (which are a generalization of Sudoku squares).
The general formula for the number N ( n , n ) for the total number of Latin squares of order n is
N ( n , n ) = n ! ( n − 1 ) ! L ( n , n ) ,
where L ( n , n ) is the number of normalized Latin squares of order n , so the formula isn't as simple as I had first thought.
Log in to reply
@Brian Charlesworth – Ah, interesting... Guess there is a name for everything... (Even if it's Latin! :0) )
It looks like the general formula for Latin squares is quite complex?
Log in to reply
@Geoff Pilling – Yes, it would appear so. There is still a lot of research being done on this topic, and the asymptotic nature of L ( n , n ) is still not fully known. Perhaps the popularity of Sudoku has fueled the scholarly interest.
@Geoff Pilling – This is an intriguing variation of the Latin square problem. As always, one good question leads to another. :)
Log in to reply
@Brian Charlesworth – Definitely!
For this, each soldier is given two characteristics:
- rank
- regiment
And they are arranged in two dimensions, on a 6x6 grid.
I wonder if you could generalize this to three characteristics in three dimensions... On a 6x6x6 grid/cube.
Log in to reply
@Geoff Pilling – Hahaha O.k., now my brain really hurts. :O
Log in to reply
@Brian Charlesworth – Ah great... My mission for the day has been achieved! ;)
@Geoff Pilling – I'm not sure how you're getting 2 characteristics. There should only be 1, namely the numbering of the color.
The typical extension to 3 dimensions is that every n squares in each dimension has the numbers 1 to n .
A
reduced Latin square(cube)
is one in which the first column/row(/height) consists of the numbers
1
,
2
,
…
,
n
in order.
There is only 1 reduced Latin square on 3 colors, and similarly 1 Latin cube on 3 colors.
Log in to reply
@Calvin Lin – I was referring to the 36 officers problem where each soldier has a rank an a regiment, no?
Log in to reply
@Geoff Pilling – That is known as "Orthogonal Latin square". We have 2 Latin squares, in which each cell is given an entry of "(first latin square entry, second latin square entry)", then every cell has a distinct entry.
@Calvin Lin – I would think that there would be 2 reduced Latin squares on 3 colors, and 4 reduced Latin cubes on 3 colors.
For example, for the square, once you have filled the first row with 1,2, and 3, for one solution you could switch the second and third rows to give you another solution, giving you 2 solutions all together.
Log in to reply
@Geoff Pilling – Sorry if I didn't make it clearer. The entire first row, and first column, (and first third dimension) has to be the numbers 1, 2, 3 ... n . So we cannot just switch the second and third rows (since then the first entry would not be in sequence).
For the Latin square on 3 colors, the bolded numbers are fixed. Then, there is a unique way to fill out the rest of the grid:
| 1 | 2 | 3 |
| 2 | 3 | 1 |
| 3 | 1 | 2 |
This can be describes as "color = x + y ( m o d 3 ) " (with suitable indexing). IE squares ( 1 , 1 ) , ( 2 , 3 ) , ( 3 , 2 ) will have the same color as they have the same x + y ( m o d 3 ) value. We see that the kth square in the first row would have color k + 0 , and the kth square in the first column would have color 0 + k , thus we get a reduced Latin square.
Similarly, for the Latin cube, the unique solution arises from "color = x + y + z ( m o d 3 ) (with suitable indexing).
Note: Proving that it is the unique solution might take a bit of case checking / trial and error. With 4 colors, there are several more possibilities. As you mentioned, we only know asymptotic bounds on L ( n , n ) .
Log in to reply
@Calvin Lin – Ah, OK, got it... I misunderstood the definition... Yes. I agree the solution would be unique then for both the square and cube (for n = 3 ).
Relevant wiki: Derangements
Consider the first row, the number of permutations for 3 colors is 3 ! = 6 . When the first row is fixed, the number of permutations in the second row is the derangement of 3, meaning the number of permutations such that they are not in their original position, denote as ! 3 = 2 . The last row is forced by the first two rows. Hence the answer is 6 × 2 = 1 2 .
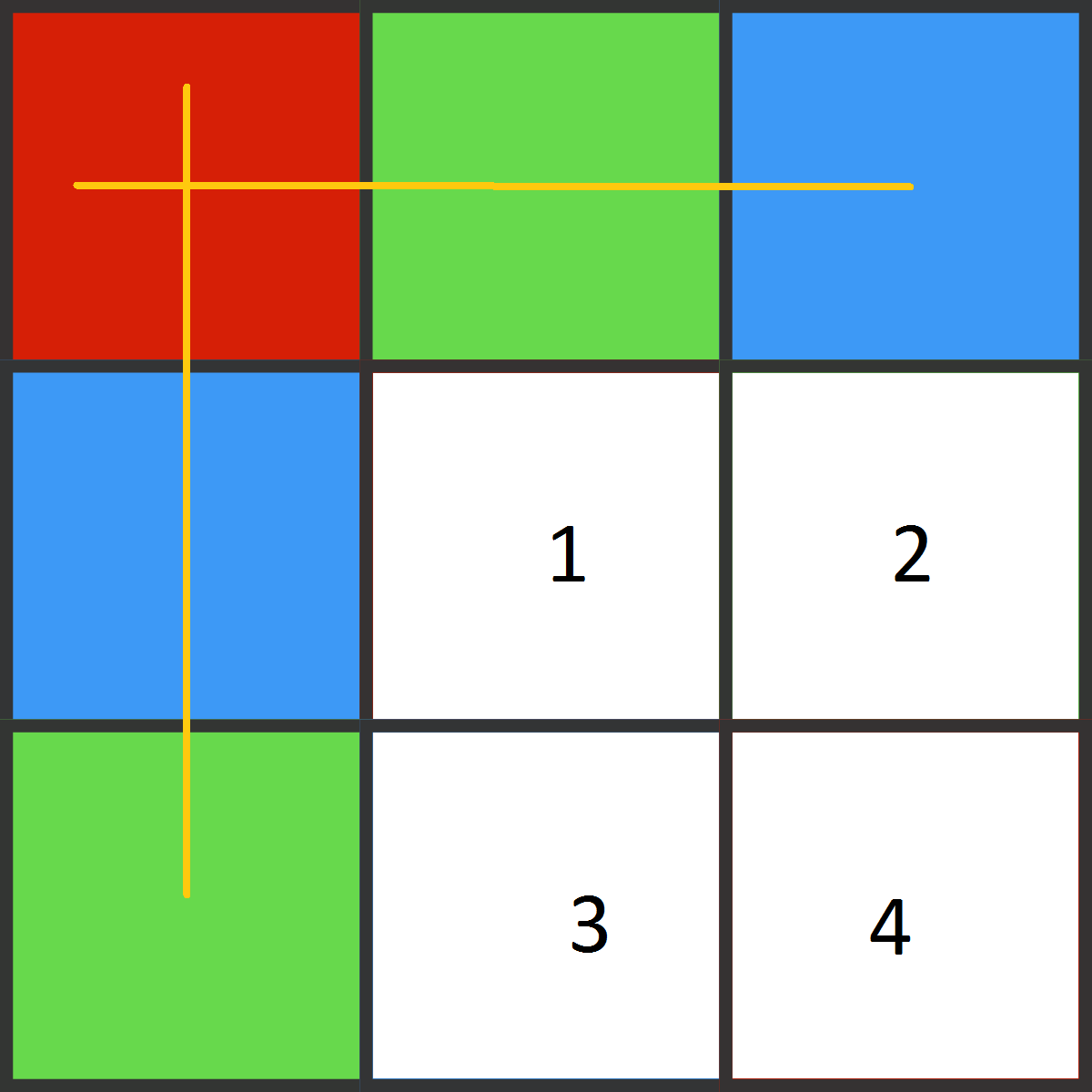
Once you paint marked squares (see picture), there is just one way to paint the rest 4 of them in order to get 3x3 grid with three colors such that each row and column has all three distinct colors. Hence, we should only determine how many ways are there to paint 5 marked squares.
There are 3 × 2 = 6 ways to paint first-column squares. Then, there are two ways of painting the left two squares knowing colors of first-column squares. Hence, there are 6 × 2 = 1 2 ways to paint 5 marked squares.
Thus, answer is 12.
This is a very detailed explanation. Nicely done!
Though this approach certainly gets really tedious if the square becomes larger.
Let the colors are c 1 , c 2 , c 3 .
Let S be set of all permutations of the above three colors.
So, S = { ( c 1 , c 2 , c 3 ) ; ( c 1 , c 3 , c 2 ) ; ( c 2 , c 1 , c 3 ) ; ( c 2 , c 3 , c 1 ) ; ( c 3 , c 2 , c 1 ) ; ( c 3 , c 1 , c 2 ) }
As per the above requirement the coloring can be done by using three distinct element from S such that position of colors in every element is different.So, here there will two such subsets these are
S 1 = { ( c 1 , c 2 , c 3 ) ; ( c 2 , c 3 , c 1 ) ; ( c 3 , c 1 , c 2 ) } and
S 2 = { ( c 1 , c 3 , c 2 ) ; ( c 2 , c 1 , c 3 ) ; ( c 3 , c 2 , c 1 ) }
From S ! we can add these elements in the rows (columns) and they can permute along rows.So there will be 3 ! = 6 ways.
Similarly from S 2 there are also 6 ways.
So, total ways = 1 2
This works, but your method would become awfully tedious if the square becomes larger, right?
Log in to reply
Yeah I agree.But I want to show some other method that's why I posted
If we consider the center square then there is 3 choices to colour that and for the 4 squares at it's 4 sides, two of different rows have 2 choices and others have only 1 choice.so total number of ways to make 3×3 colour cube = 3ç¹×2ç¹×2ç¹=3×2×2=12
This is probability question, where number of angles are 4 (90, 180, 270, 360/0) Placing each color diagonally can be done in 3 ways
So total number of ways of arranging it is 4c3= (4 * 3 * 2) / (2 * 1) = 12
Let's consider the three colors as permutation-based objects. In the first row, the colors can be arranged in 3! = 6 ways - since it is the first row, the colors within the first row could be arranged in any way. In the second row, the colors can be arranged in a very limited way, since we have some of the 6 ways having a same color on the column or row. So, the colors within the second row could be arranged by (3 - 1)! = 2 ways. In the third row, the colors wouldn't be able to arrange themselves freely, since we're preventing the colors from other columns or rows to be similar. So there are only (3 -2)! ways = 1 way to arrange the colors in the third row. Therefore, we have 6 x 2 x 1 = 12 ways to distinctively color the 3 x 3 square without having a same color in either row or column.
For a 3 by 3 grid it is quite easy to calculate the number of ways when 3 colours are used. Each colour can be used once on the diagonal, with the other two colours each occupying a corner with the two adjacent squares filled with the other colour. (Think also of chess and the move of a knight.) This yields 3 ways. Each of these 3 ways are rotated: 0 degrees, 90 degrees, 180 degrees and 270 degrees. This gives another 4 ways for each of the 3 colours. 3 x 4 = 12 ways in total.
hint : this have something to do with derangement , would be more challenging for 4*4 or more .
Isn't this just the number of Latin squares of order 3?
As the problem is stated, 18 is the correct answer. The problem asks about each row or column, not and column. For each row or column, there are 3! = 6 arrangements, and there are 3 rows (or columns).
Ah, very perceptive, thanks! (I've clarified the wording)