Pairs of Close-Together Points

Lemma 1: Given 4 points on the plane, let the maximum distance between 2 points be $M$ and the minimum distance between 2 points be $m$ , then $\frac {M}{m} \geq \sqrt{2}$ .

Proof: If the convex hull consist of 3 points, then we can show that $\frac {M}{m} \geq \sqrt{3}$ . Let $O$ be the point contained within the convex hull. Then we can find a triangle where $\angle AOB \geq 120 ^ \circ$ . WLOG, let $OA \geq OB$ , so $\angle OAB \leq 30^\circ$ . Then $\frac {AB}{OB} = \frac {\sin \angle AOB} {\sin \angle OAB} \geq \frac{ \sin (2 \angle OAB)}{\sin \angle OAB} \geq 2 \cos \angle OAB \geq 2 \cdot \frac {\sqrt{3} }{2} = \sqrt{3}$ . $_\square$

If the convex hull consists of 4 points, then one of the angles is at least $90 ^ \circ$ . Let it be $\angle ABC$ . Let $AB \geq BC$ , so $\angle BAC \leq 45 ^ \circ$ . Then, $\frac {AC} {BC} = \frac { \sin \angle ABC} {\sin \angle BAC} \geq \frac { \sin ( 2\angle BAC)} { \sin \angle BAC} = 2 \cos \angle BAC \geq 2 \cos 45^\circ = \sqrt{2}$ .

Lemma 2: Given a graph with 6 vertices which are connected by 13 edges, there must be a complete graph on 4 vertices.

Proof: Since there are at most ${6 \choose 2} = 15$ edges, there are 2 edges that are not connected. If these 2 edges share a common vertex V, then any 4 of the other points will work. If the 2 edges do not share a common vertex, take 1 vertex from each of these pairs, and the other 2 vertices. $_\square$

For the original set of 6 points, draw an edge in if the length is more than $\sqrt{2}$ . If there are at least 13 edges, then by Lemma 2, there exist 4 points each of which are distance $\sqrt{2}$ apart. By Lemma 1, the maximal distance would be greater than $\sqrt{2} \times \sqrt{2} = 2$ , which contradicts the assumptions. Hence, there are at most 12 such pairs.

It remains to show that 12 is possible. Let $ABC$ be an equilateral triangle of edge length 2. Take $A_1, B_1, C_1$ just within the triangle, and close to the respective vertices. This gives us $3 \times 4 \times 2 \div 2 = 12$ edges with length close to 2. Hence we are done.

Construction：an equilateral of length 2 and its duplicate Proof：if there are at most 2 pairs violating, then there are four points which are strictly greater than sqrt2 apart, which can not occur(there must be an angle>=90)

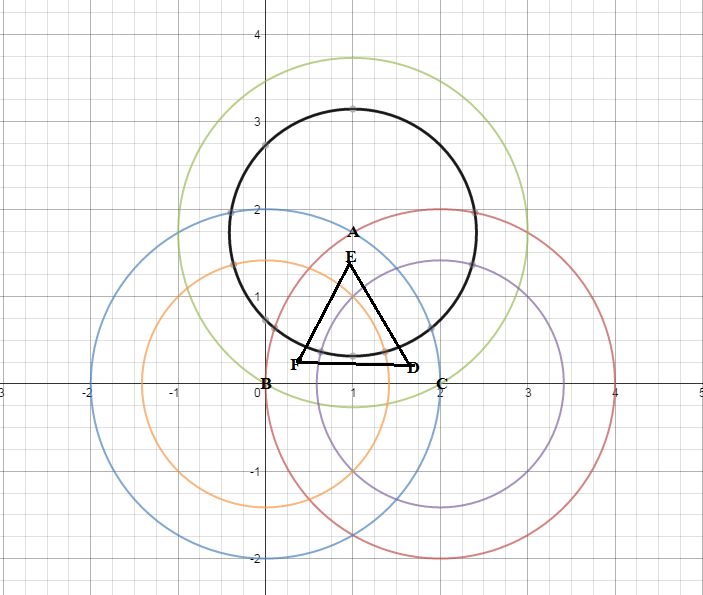
I solve it slight geometrically and by making some assumptions . first putting the point A then the point B will be in between the circle having center A and radius 2. assuming B on the circle (as it is greater than sqrt(2) ) after drawing a circle having center B and radius 2 we can say that other 4 points will lie in the common region of the two circles. then assuming the third point C in one of the intersection point and drawing another circle of center C and radius 2 , it can be said the other three points will be in the common region of the three circles (other wise the distance between one of these three point (A,B,C) and any of the other points will more than 2). then drawing three circles of radius sqrt(2) having center at A, B, C respectively. to keep maximum pair, we need to put D, E, F as in the picture where DE, EF, DF all are greater than sqrt(2).

hence the possible pairs having distance more than sqrt(2) is (A,B), (A,C), (B,C), (B,D), (B,E), (A,F),(A,D),(C,E),(C,F), (D,E),(E,F),(D,F)

no of pairs = 12.

Let $p$ be the number of pairs of points which are strictly greater than $\sqrt{2}$ apart. Define a $hole$ be a point position on a plane if there is at least one point in it.

Divide into 4 cases:

(a) There is 1 hole. All the 6 points lie in the hole. $p=0$ .

(b) There are 2 holes. There are 3 possibilities. (i) 1 point is in one hole and the other 5 points are in the other hole. $p=1\times5=5$ . (ii) 2 points are in one hole and the other 4 points are in the other hole. $p=2\times4=8$ . (iii) 3 points are in each hole. $p=3\times3=9$ . [All these are achievable if the 2 holes are 2 units apart].

(c) There are 3 holes. There are 3 possibilities. (i) 1 point lies in one hole, 2 points lie in the next hole, 3 points lie in the last hole. $p=1\times2+2\times3+3\times1=11$ . (ii) 1 point lies in one hole, 1 point lies in the next hole, 4 points lie in the last hole. $p=1\times1+1\times4+4\times1=9$ . (iii) 2 points lie in each hole. $p=2\times2+2\times2+2\times2=12$ . [All these are achievable if the 3 holes are the vertices of an equilateral triangle with side length 2].

(d) There are at least 4 holes. First, we establish a lemma. Lemma : Given at least 4 points on a plane, no 3 of them are collinear, then 3 of them must form an obtuse or right triangle. Proof : First, we make a simplification. If the lemma holds true for 4 points, then it holds true for more than 4 points (since we can choose the arbitrary 4 points in a set of more than 4 points). It suffices to prove the lemma for 4 points. If the 4 points form a convex quadrilateral, their internal angle sum $=360^\circ$ and since there are 4 internal angles, the average of the angles $=\frac{360^\circ}{4}=90^\circ$ . By Mean Value Theorem, at least one angle is greater than or equal to $90^\circ$ . The 3 points that form the angle will form an obtuse triangle or a right triangle. If the 4 points form a non-convex quadrilateral $ABCD$ , wlog $ABCD$ is concave at point $C$ . $\angle ACB+\angle ACD>180^\circ$ . By the Mean Value Theorem, one of the angles are greater than $90^\circ$ . The 3 points that form the angle will form an obtuse triangle. This completes the claim. Let $\bigtriangleup ABC$ be the obtuse or right triangle among the set of points, such that $\angle ABC\geq90^\circ$ . By Pythagorean Inequality, $AB^2+BC^2\leq AC^2\leq2^2=4$ . Since $AB>\sqrt{2}$ and $BC>\sqrt{2}$ , $AB^2+BC^2>4$ , a contradiction. For the case where 3 points are collinear, consider 3 points A,B,C, where B lies between A and C. $AB+BC=AC\leq2$ . By Mean Value Theorem, $AB$ or $BC$ is smaller than or equal to $\frac{2}{2}=1$ . This will contradict the fact that any 2 points are at most distance 2 apart. It is impossible to have more than 3 holes.

Combining all cases, $p_{max}=12$ .

We can assume that the set of six points at most a distance $2$ apart must all be located within a Reuleaux Triangle circumscribed around an equilateral triangle of side length $2$ .

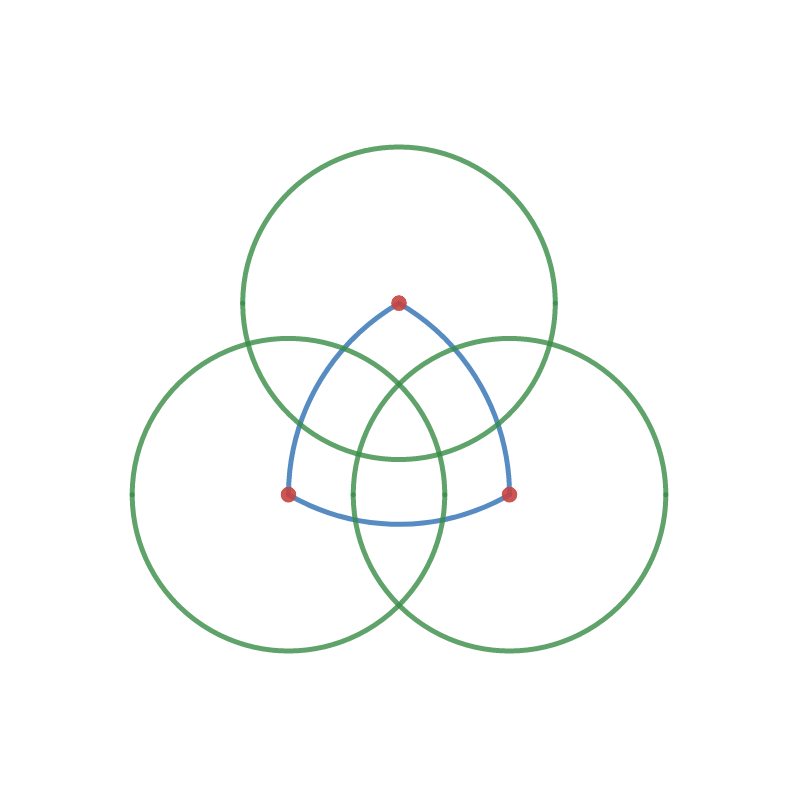
In terms of the diagram above, all six points must be located somewhere within or on the Reuleaux triangle shown (in blue) constructed from an equilateral triangle of side length 2. If we are to maximize the distances between each pair of points, we can assume that the corners are occupied by three of them (shown in red). No matter where within the Reuleaux triangle we place the three remaining points, it's obvious that they will be within at least one of the green circles of radius $\sqrt{2}$ , and therefore at a distance of less than $\sqrt{2}$ from one of the points on the corners. The best we can do, then, is to place the three points each in exactly one of the circles, making the number of pairs of points at a distance greater than $\sqrt{2}$ equal to $\boxed{12}$ .

(Note: Sorry Calvin, I don't think my solution is proper. Though it wasn't just a guess, but rather, I tried to think and project a strategy for the placement of the points.) The best way to arrange the points is place 4 points on the corners of the square. Place the other 2 points on one corner to minimize the no. of pairs reduced and such that the distance of the 3 points in one corner is at least the distance required. There are 5C2= 15 pairs. There are only 3C2= 3 pairs that do not satisfy the distance asked. Therefore, 15-3=12 pairs that are strictly greater than sqrt(2). Since this strategy maximized the number of pairs that satisfy the condition, the most number of pairs is 12.

Logical Deduction:

In all polygons, only triangle's vertices are all directly connected by its side. In all other convex polygons, the distance between non-adjacent vertices are always larger than its side length.

Hence, in order to ensure any 2 points are at most distance 2 apart, all polygons except for triangle must have a side length smaller than 2.

Considering a square, which is a regular 4 sided polygon, its side length is $\sqrt{2}$ in order for its diagonal distance to be 2. If the number of sides increases, the side length of a regular polygon has to reduce further (which means definitely smaller than $\sqrt{2}$ ) to make sure the furthest distance between any 2 points is 2.

Therefore, only in a triangle configuration, all pairs of points will have a distance strictly more than $\sqrt{2}$ . In any other configuration, some pairs formed by adjacent vertices have to have a distance of less or equal to $\sqrt{2}$

Now, we apply this into the case of 6 points.

1. Construct a equilateral triangle ABC with side length 2.

2. Place 3 points exactly on its vertices.

3. Place another 3 points infinitely close to 3 different vertices.

In this way, only the pairs between the point that is very near to the vertex and the point exactly on that particular vertex has a distance smaller than $\sqrt{2}$ . In total, there are 3 such infinitesimally close pairs of points. (One at each vertex)

Total number of pairs $=5+4+3+2+1=15$

Number of pairs of points which are strictly greater than $\sqrt{2}$ apart $=15-3=12.$

In all other configurations, due to the pairs formed by adjacent vertices, more pairs of points with distance less or equal to $\sqrt{2}$ will occur. Hence, 12 is the most number of pairs of points which are strictly greater than $\sqrt{2}$ apart.