Going down the parabolic slide
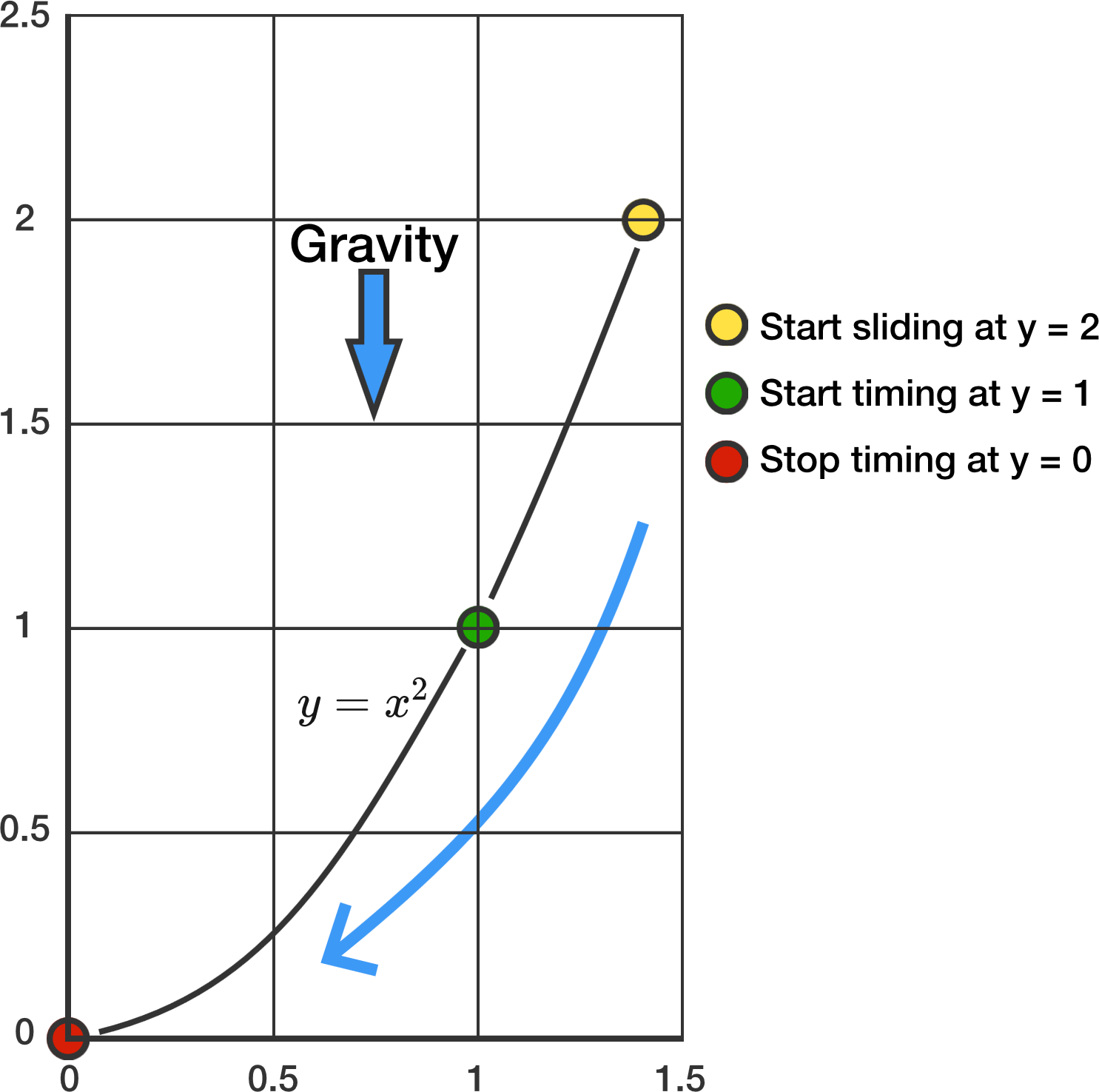
Under the influence of gravity ( g = 1 0 m / s 2 ), a bead slides down a friction-less wire in the shape of the curve y = x 2 . The bead begins from rest at ( x , y ) = ( 2 m , 2 m ) .
How much time (in seconds) does it take the bead to travel from the point ( 1 m , 1 m ) to the origin ( 0 m , 0 m ) (to 2 decimal places)?
The answer is 0.27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions

it would be more precise to ask for two decimal places in the answer because it initially rejected my answer of 0.2
Log in to reply
Good suggestion. I made the edit
Log in to reply
Thanks. I see that this problem has been edited. Those who previously answered 0.2 has been marked correct.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator (and eventually staff) who can fix the issues.
Log in to reply
@Brilliant Mathematics – yeah done !
@Brilliant Mathematics – i entered 0.266 (it is the real answer ) and it told me wrong , plz help @Steven Chase @Brilliant Mathematics plz mark me as a solver !
Log in to reply
@A Former Brilliant Member – 0.27 is an approx, 0.266 is correct indeed mark me as a solver ! i'm really frustrated @Josh Silverman sir plz !
Log in to reply
@A Former Brilliant Member – I'm fine with you getting credit, but I don't have the ability to change it. Just for the record though, the problem does ask for the answer to 2 decimal places.
Log in to reply
@Steven Chase – that's what i gave it first , i wrote 0.26 only because it says 2 decimal ! got rejected then wrote 0.266 and then 0.4567 (for fun) and boom , i was rejected for all !
Log in to reply
@A Former Brilliant Member – Ok, but the general convention is to round, not to truncate. Anyway, let's wait for the staff to respond.
@A Former Brilliant Member – Hi @shubham dhull , I agree that you probably got it right since you indeed entered 0.26. I totally disagree that entering 0.4567 is "fun". It appears you also entered 0.433 which I also don't think is fun. In this case, I'm going to award you credit. In the future, if the problem writer says to go to two decimal places, you should know to round your answer.
Log in to reply
@Josh Silverman – okay to prove my point i will upload a solution ! and plz belive me i just entered a random number the third time i don't know what it was !
The Lagrangian of the system is the kinetic energy minus the potential:
L = 2 1 x ˙ 2 + 2 1 ( 2 x x ˙ ) 2 − 1 0 x 2
Solving the Euler-Lagrange equation for x ¨ ;
d t d ∂ x ˙ ∂ L = ∂ x ∂ L
it yields:
x ¨ = 1 + 4 x 2 − ( 2 0 x + 4 x x ˙ 2 )
I felt the best way to find the time taken for the object to reach point ( 0 , 0 ) from point ( 1 , 1 ) when released from ( 2 , 2 ) is to find the velocity at point ( 1 , 1 ) by simulating from ( 2 , 2 ) to ( 1 , 1 ) , and then simulating (with time = 0 again) with the new initial velocity from ( 1 , 1 ) to ( 0 , 0 ) . I used the Explicit Euler numerical method to do this; by numerically integrating the acceleration to find the position and ultimately the time it takes to reach the bottom. Here's the code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
|
my name is still not updated in the solver's list , still , just to show my approach here is my solution

@Josh Silverman i have added the solution