Parallel and perpendicular
 {
x
2
+
y
2
=
1
x
2
−
2
x
y
+
3
y
2
=
k
{
x
2
+
y
2
=
1
x
2
−
2
x
y
+
3
y
2
=
k
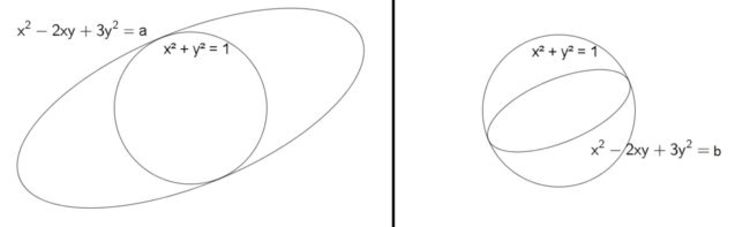
The above two curves touch each other at k = a and k = b where a > b . Find the value of ⌊ b 1 0 0 0 a ⌋ .
The answer is 5828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Solve the simultaneous equations, x 2 − 2 x y + 3 y 2 = k ( x 2 + y 2 ) which we can rewrite it as a quadratic in x : ( 1 − k ) x 2 − 2 x y + ( 3 − k ) y 2 = 0 . As the two curves touch each other, the discriminant is zero. Hence 4 y 2 − 4 ( 1 − k ) ( 3 − k ) y 2 = 0 which means that k 2 − 4 k + 2 = 0 and hence k = 2 ± 2 . Thus b a = 2 − 2 2 + 2 ≈ 5 . 8 2 8 . So ⌊ b 1 0 0 0 a ⌋ = 5 8 2 8
Why should the discriminant be zero?
Log in to reply
As the two curve TOUCH each other, meaning that there having equal real roots for the equation and hence the discriminant is zero.
Log in to reply
But they touch each other at two different points.
Log in to reply
@Saurabh Chaturvedi – For each k , there is a point.
Log in to reply
@Chan Lye Lee – But the figure shows 2 points of intersection for each k.
Log in to reply
@Saurabh Chaturvedi – Sorry for previous respond. My mistake.
Any point lying on the circle would be of form * ( c o s ( x ) , s i n ( x ) ) * so just satisfy the point in equation 2 we get
s i n ( 2 x ) + c o s ( 2 x ) = 2 − k we want now it to be satisfied for only 2 points. therefore applying boundary line condition
2 − k = s q r t ( 2 )
2 − k = − s q r t ( 2 )
k = 2 − s q r t ( 2 )
k = 2 + s q r t ( 2 )
well simplest and most elegant.Exactly what i thought of.Just the fact that they put gint function everywhere gets my answer wrong.
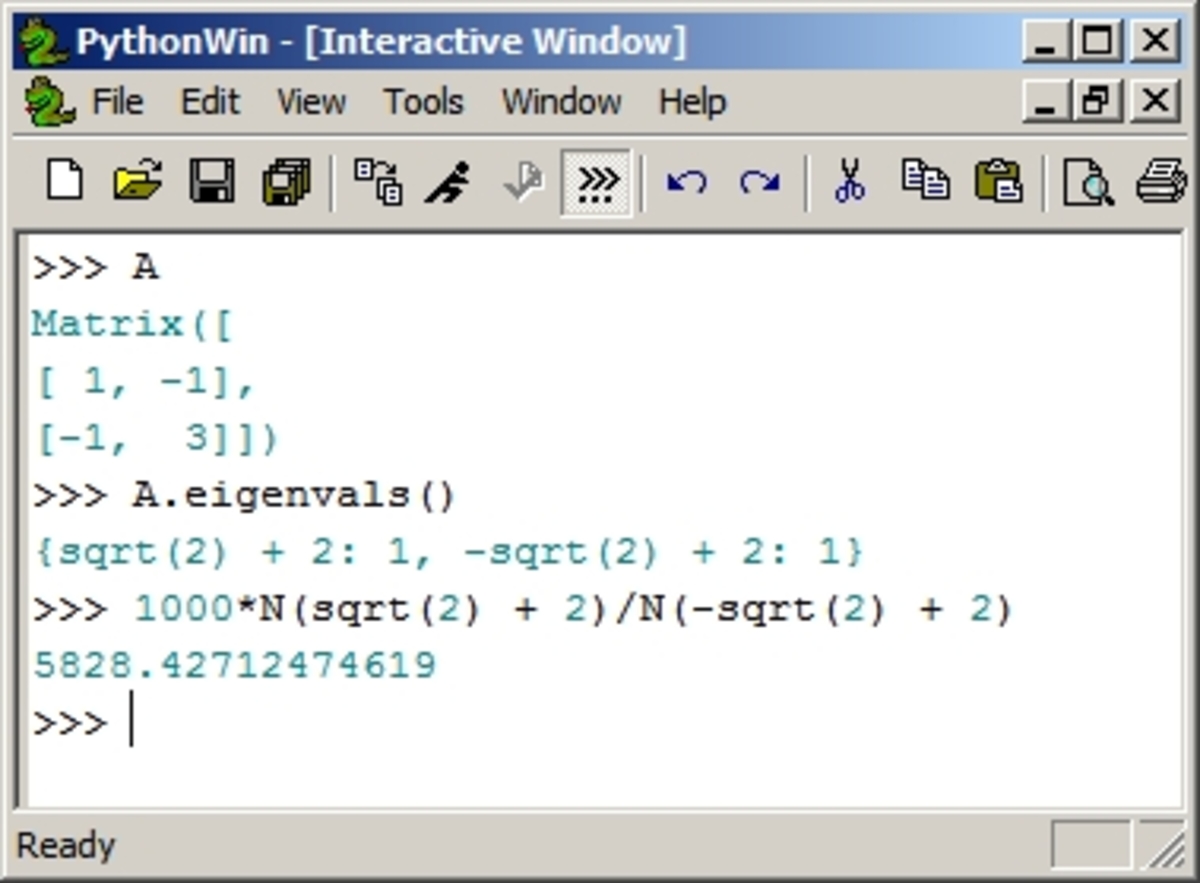
Like Dr Bretscher's, but using a symbolic algebra system. He reminded me of theory that I hadn't seen since the 70's when I studied principal components, just a day or two ago.
Pls mention whether it is GIF or LIF.I got the right answer but......
Log in to reply
GIF or LIF?
⌊ ⋅ ⌋ is the standard notation for Greatest Integer Function.
⌈ ⋅ ⌉ is the standard notation for Least Integer Function.
The symmetric matrix of the quadratic form q ( x , y ) = x 2 − 2 x y + 3 y 2 is A = [ 1 − 1 − 1 3 ] with the eigenvalues a = 2 + 2 and b = 2 − 2 . Now b a = 3 + 2 2 ≈ 5 . 8 2 8 . The answer we seek is 5 8 2 8