Parallelogram Riddle
A parallelogram is divided into four regions that share one common point, as shown below.
Is the total blue area always equal to the total yellow area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Note that if we use signed areas, we get this property to hold true for all points in the plane.
Log in to reply
umm.. what is directed areas? :D
Log in to reply
Oops, better terminology is signed areas. Signed areas allow the usage of negative areas if they are oriented oppositely to some areas.
Log in to reply
@Sharky Kesa – oh thanks for explaining. Btw is your name really sharky?
Log in to reply
@Mehdi K. – Nope, it's a pseudonym. :D
Wow, just wow!
Very elegant !
This problem is making the assumption that the other ends of the 4 intersecting lines are in the corners of the quadrilateral. It is possible to have 4 lines share a common point within the quadrilateral and this situation not be true.
Relevant wiki: Length and Area - Composite Figures
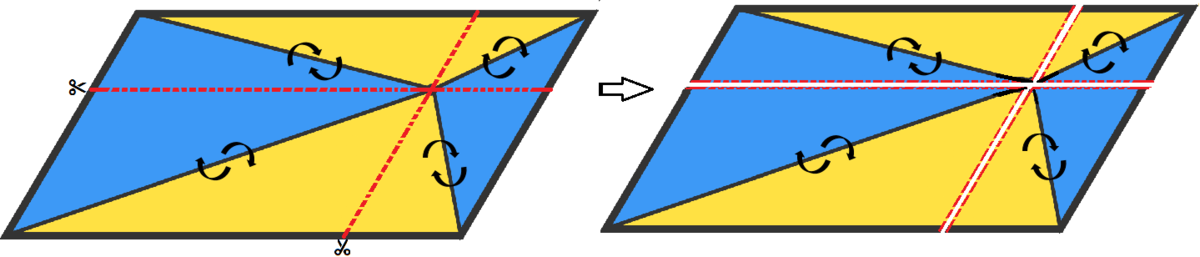Draw dotted red parallel lines as in the above diagram, it will divide larger parallelogram into four smaller parallelograms. Clearly in each of the smaller parallelograms, the diagonal divides equal region of yellow area and blue area.
Therefore, total blue area always equal to the total yellow area
A t r i a n g l e = 2 b × h
Therefore the combined area of both yellow triangles must be:
A y e l l o w = 2 b × h 1 + 2 b × h 2 = 2 b × ( h 1 + h 2 )
h 1 + h 2 equals the height of the entire parallelogram and b is the base of the parallelogram, so the yellow area never changes no matter where you set the common point. Therefore the blue area also never changes: A b l u e = A p a r a l l e l o g r a m − A y e l l o w
If the common point was the intersection point of the 2 diagonals of the parallelogram we would know that both the yellow and the blue area would be equal. Since the relation of their areas never changes we can infer that they are always equal.
To solve this problem I split up the shape into more triangles. I checked how many triangles fit into the already existing triangles. I could have also tried to measure it. I would rate this problem a 1 because I did these things in class before so I already had it clear what to do. While solving this problem I felt like it wasn't hard at all. I enjoyed it.
Start with the common point in the centre. Obviously each triangle will be a quarter of the area of the parallelogram. You can then move the common point to any point within the parallelogram by a combination of two moves:
- A horizontal move, which shears the yellow triangles and therefore preserves their area, and hence the combined area of the blue triangles
- A move parallel to the sloping sides, which likewise preserves the area of the blue triangles and hence the yellow triangles.
Hence the combined area of the two blue triangles, or of the two yellow triangles, will always be half the area of the parallelogram.
Given that sides are parallel ,diagonals intersect it into 1/2equal areas (colors)
As shown above, for any interior point in any parallelogram, we can always draw the lines parallel to its sides, which would partition it into 4 smaller parallelograms. The 4 adjoining lines will then become the diagonals, bisecting the areas into blue and yellow. Thus, any point in the parallelogram will always partition equal blue and yellow areas.