Parellelogram Geometric Progression

The red and green parallelograms are similar since they are each made of two congruent triangles, and a red triangle is similar to a green triangle. Therefore, if we let the base of the red parallelogram be $b$ , and its height be $h$ , then the base and height of the green parallelogram are $bk$ and $hk$ for some number $k$ .

Now we can calculate the areas of each colored region, so the sequence $bh$ , $bhk$ , $bhk^2$ forms a geometric progression. This means that $k$ is the common ratio for this progression.

The base of the entire parallelogram is $b+bk = b(k+1)$ , and the height is $h+hk = h(k+1)$ . Therefore, its area is $bh(k+1)^2 = 2009 \implies bh = \frac{2009}{(k+1)^2}$ . Since $bh$ and $bhk$ are both integers, $k$ must be a rational number in the form $\frac{x}{y}$ , where $x$ and $y$ are positive integers.

$bh = \frac{2009}{(\frac{x}{y}+1)^2} = \frac{2009}{\frac{(x+y)^2}{y^2}} = \frac{2009y^2}{(x+y)^2}$

$2009 = 7^2*41$ , and $x+y \ge 2$ . Therefore, for this fraction to be an integer, $x+y = 7$ . We have $bh = \frac{2009y^2}{7^2} = 41y^2$ . The largest value of $y$ is $6$ , so the maximum value of $bh$ is $41*36 = \boxed{1476}$ .

Note: There is no way to get the fraction to be a multiple of $49$ . For this to happen, $y^2$ must contain a factor of $41$ , so $y^2 = 41n$ for some integer $n$ . $(x+y)^2 > 41n$ , so $x$ must be chosen to make $(x+y)^2$ be a multiple of $41n$ , which means there is now an extra factor in the denominator. Therefore there is no way to make this work.

Let the green area be a positive integer $a$ . To maximise the red area, we'll need to minimise $a$ with the restriction that the coloured areas are distinct positive integers that sum to 2009.

The the total area is $a(1+2r+r^2)=a(1+r)^2=2009=7^2\cdot 41$ .

This means $r=7\sqrt{\frac{41}{a}}-1$ and so $ar=7a\sqrt{\frac{41}{a}}-a=7\sqrt{41a}-a$ .

As $a$ is a positive integer and $ar$ is a distinct positive integer, $a$ must contain $41$ as a prime factor.

So the minimum solution has $a=41$ and $1+r=7$ , meaning $r=6$ . Therefore, the red area is $ar^2=41\cdot 36=1476$ .

General solution

The sides of the parallelogram are divided in the same ratio $a:b$ (assume no common factors). Thus the areas have ratios $\text{red} : \text{blue} : \text{green} = ca^2 : cab : cb^2$ for some constant $c$ . If $a,b,c \not= 0$ and $a \not= b$ this is a geometric progression with factor $b/a$ .

The total area of the parallelogram is $A = c(a+b)^2$ . In order to have integer areas, we need $a,b,c$ to be integers. Thus we find the following recipe for solving the problem:

• Factor the given area $A$ in the form $A = cx^2$ , with $x$ as large as possible.

• Let $a = x - 1$ and $b = 1$ .

• Then the red area is $ca^2$ .

In this case, $A = 2009 = 41\cdot 7^2$ , so that $x = 7$ , $a = 6$ , $b = 1$ , $c = 41$ , and $\text{red} = ca^2 = 41\cdot 6^2 = 1476.$

Let red area be $A_1$ , blue area $A_2$ , green area $A_3$ . We know that:

$\frac{A_1}{A_2}=\frac{A_2}{A_3} \Rightarrow A_2=\sqrt{A_1A_3}$

And also:

$A_1+2A_2+A_3=2009$

Therefore:

$A_1+2\sqrt{A_1A_3}+A_3=2009$

$(\sqrt{A_1}+\sqrt{A_3})^2=2009$

$\sqrt{A_1}+\sqrt{A_3}=7\sqrt{41}$

So $A_1$ and $A_3$ must be multiples of $41$ , and, since $A_3$ can't be zero, the maximum of $A_1$ must be $\boxed{1476}=36\cdot41$ , in order to have:

$6\sqrt{41}+\sqrt{41}=7\sqrt{41}$

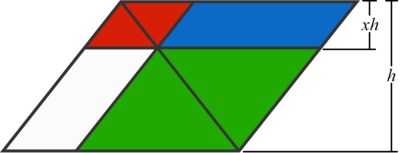Since the diagonal divides the big, red and green parallelograms into halves, it is obvious that the area of the blue parallelogram is same as that of the white parallelogram.

Let the height of the big parallelogram be $h$ and that of the red parallelogram be $xh$ , where $x < 1$ . Since the shapes of the red and green parallelograms are similar to that of the big parallelogram their areas are directly proportional to their heights. That is:

$\begin{cases} A_{big} = 2009 \\ A_{\color{#D61F06}red} = 2009x^2 \\ A_{\color{#20A900}green} = 2009(1-x)^2 \\ A_{\color{#3D99F6}blue} = \frac {2009}2 \left(1-x^2 - (1-x)^2\right) = 2009x(1-x) \end{cases}$

Note that $\dfrac {A_{\color{#3D99F6}blue}}{A_{\color{#D61F06}red}} = \dfrac {A_{\color{#20A900}green}}{A_{\color{#3D99F6}blue}} = \dfrac {1-x}x$ , the common ratio.

We note that $2009 = 7^2 \times 41$ . For $A_{\color{#D61F06}red} = 2009x^2$ to be an integer, $x = \frac n7 < 1$ , where $n$ is a positive integer. Then we have:

$\begin{cases} A_{\color{#D61F06}red} = 41n^2 \\ A_{\color{#20A900}green} = 41(7-x)^2 \\ A_{\color{#3D99F6}blue} = 41n(7-n) \end{cases}$ , which are all integers.

We note that when $n=7$ , $A_{\color{#D61F06}red} =2009= A_{big}$ and $A_{\color{#20A900}green} = A_{\color{#3D99F6}blue} = 0$ . Therefore, $A_{\color{#D61F06}red}$ is maximum when $n=6$ ; that is $\max(A_{\color{#D61F06}red}) = 41\times 6^2 = \boxed{1476}$

Because the figure isn't drawn to scale, there is no reason that the red area must be smaller than the blue area, which is our key to solving the problem. Say the area of the red section is equal to a, and the ratio of the blue section's area to the red section's area is equal to d. Because the areas are in a geometric progression, we must have $a + a d + a d^2 + ad = 2009$ . Note that the lefthand side is equal to $a (d+1)^2$ , so $a = \frac{2009}{(d+1)^2}$ , and because a is an integer, the expression on the right-hand side must also be an integer. $2009 = 41*49 = 41 * 7^2$ , so we must have $d+1 = \frac{7}{n}$ for some integer n, and thus $a = 41 n^2$ . Because $a<2009$ , $n<7$ , and the value $n=6$ maximizes a. So $a = 41 * 36 = 1476$ .

R:=red area, B:=blue area, G:=green area. r is the common ratio. R,B,G are integers. R, B and G form a geometric progression, so: B = r R, G = r B = r^2 R. The area of the entire figure is 2009 = R + 2 B + G = R + 2 r R + r^2 R = R (1 + 2 r + r^2).

The primes of 2009 are: 7 and 41. If If you try R = 7 you get: 1 + 2 r + r^2 = 2009 / 7 = 287. If you transform the equation you get: 1 + 2 r + r^2 = (r+1)^2 = 287. So r = 15,941... That doesn't work because r has to be an integer.

Do the same with R = 41 and you get (r+1)^2 = 2009 / 41 = 49. So r = 6. Now R = 41, B = 41 * 6 = 246 and G = 246 * 6 = 1476.

To answer the question you have to switch the green area an the red area and you see that the maximum possible area of the red (or the green) section is 1476 .

Let r, g, b be the area of the colored shapes, and k be the constant in the geometric progression.

then we easily get these equations:

r+2b+g=2009

r = kb =kkg

and thus when we substitute

kkg+2kg+g=2009=g(kk+2k+1) <=>2009/(kk+2k+1)=g

we know g is an integer and thus (kk+2k+1) must be a factor of 2009:

2009

287

49

41

7

1

We want r to be the biggest so we brute force these value to find a positive rational as solution to (kk+2k+1)={factor} where 2009k/{factor}=b is an integer and 2009kk/{factor}=r is an integer (if there were multiple solutions take the one which yield the biggest r).

so we find the solution {factor} = 49, k=6, g=41, b=246 and finally r = 1476

Let the red, blue, and green areas be $r,b,g$ , respectively. They are in a geometric progression in that order, but, because we are maximizing $r$ , that progression will be decreasing. To make things easier, let's reverse the order of the geometric progression, so that we have $r=gk^2,b=gk$ , for some $k>1$ . Note that, because the three areas are integers, $k$ is rational.

Also, note that the white area and the blue area are equal, so the total area of the parallelogram (which is 2009) can be written as $2009 = r + 2b + g = gk^2 + 2gk + g = g(k^2+k+1) = g(k+1)^2$ . Now we compare the factorization of $2009=41\cdot7^2$ with this final expression.

Non-Rigorous Way

In the factorization of 2009, there's an integer times a square, and in our expression, we also have that. Wouldn't it be pretty cool if those components lined up? Let's try it: $g=41 , (k+1)^2=7^2 \Rightarrow k=6$ . If this is the green area, the red area is just $gk^2=41\cdot6^2=1476$ , which is the right answer.

Actual Justification

The method above doesn't show that 1476 is the maximum value of the red area, just that it's a possible value. To do that, we can go back to the equation $41\cdot7^2 = g(k+1)^2$ and notice that, if we divide both sides by g, we get $\frac{41\cdot7^2}{g} = (k+1)^2 \Rightarrow k+1 = \sqrt{\frac{41\cdot7^2}{g}} = 7\sqrt{\frac{41}{g}} \Rightarrow \frac{k+1}{7} = \sqrt{\frac{41}{g}}$

Because $k$ is rational, so is the left side of the final expression. Therefore, the right side is also rational. But, the right side is only rational if and only if $\frac{41}{g}$ is the square of a rational. However, because 41 is prime and $g$ is an integer, we must have $g=41\cdot c^2$ for some positive integer $c$ . Plugging in, that gives $\frac{k+1}{7} = \sqrt{\frac{41}{41\cdot c^2}} = \frac{1}{c}$ .

Rearranging, we have $k=\frac{7}{c}-1$ . Remember, $g=41c^2$ . So, plugging all this into $r$ , we get $r=gk^2=(41c^2)(\frac{7}{c}-1)^2 = (41c^2)(c^{-2})(7-c)^2=41(7-c)^2$ . It is clear that the minimal value of $c$ gives the maximum value of $r$ . $c$ is a positive integer, so $c=1 \Rightarrow r=1476$