Parallelograms in the Intersections
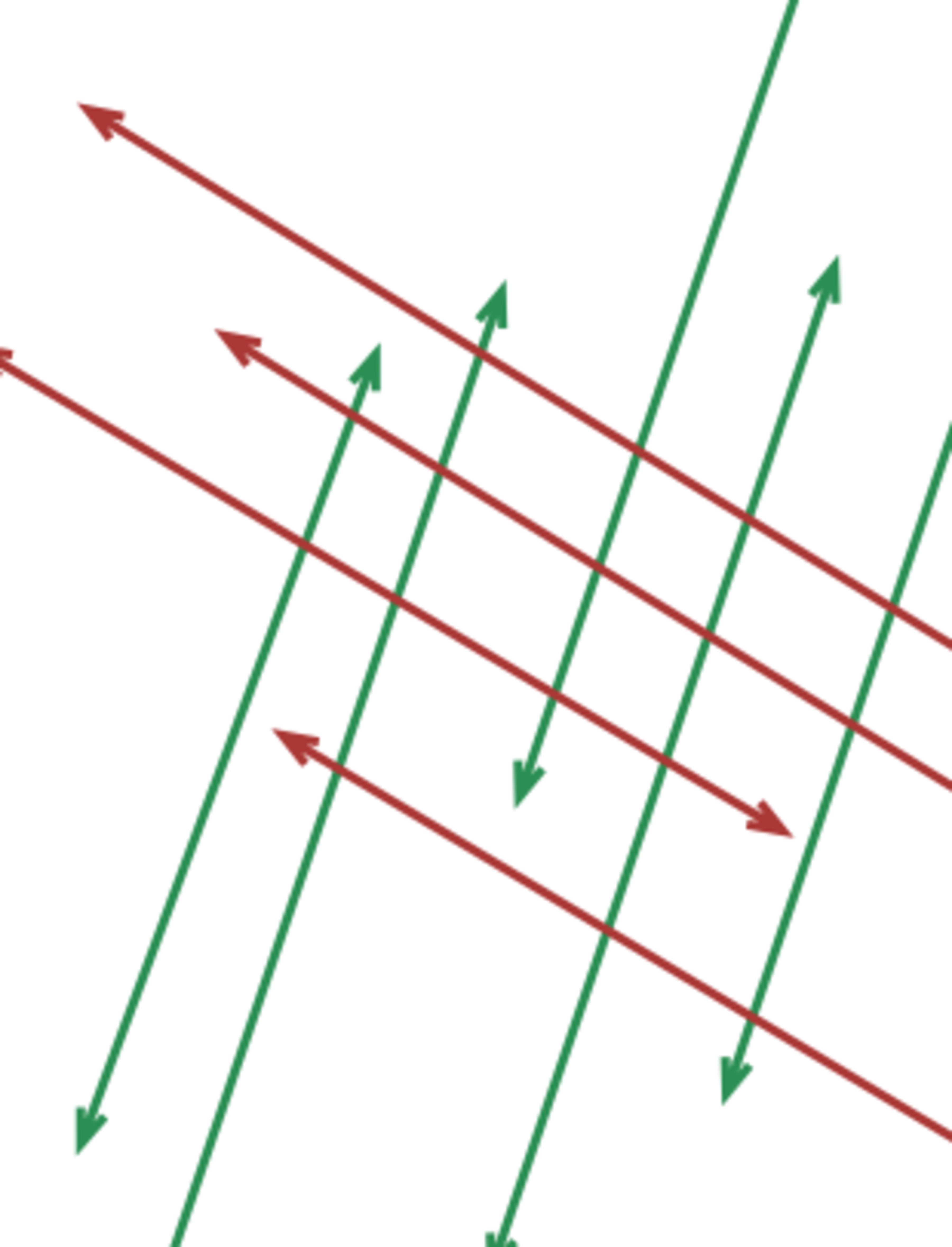 Each of the lines is extended infinitely in both direction
Each of the lines is extended infinitely in both direction
Let denote the number of parallelograms that are formed when a set of parallel lines intersect a set of parallel lines.
Find .
Inspiration & Image Credit .
The answer is 867085000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Claim: Number of parallelograms formed C ( m , n ) = m C 2 × n C 2
Proof: Choosing 2 lines from m parallel lines and 2 lines from n parallel lines would give an unique parallelogram(parallelogram is a quadrilateral formed by 2 pairs of parallel lines). Conversely, every parallelogram can be obtained by choosing these pairs of parallel lines. This establishes the bijection between "parallelogram" and "choose 2 lines from m, choose 2 lines from n". □
Thus, ∑ C ( 1 0 1 , n ) = 1 0 1 C 2 × n C 2 . Factoring 1 0 1 C 2 out of summation, the other term is
2 C 2 + 3 C 2 + . . . + 1 0 1 C 2 . Write 2 C 2 as 3 C 3 as both are 1 . Now using the identity n C r − 1 + n C r = n + 1 C r ,
we get
3 C 3 + 3 C 2 + 4 C 2 + . . . . + 1 0 1 C 2 = 4 C 3 + 4 C 2 + . . . . + 1 0 1 C 2 = . . . . = 1 0 1 C 3 + 1 0 1 C 2 = 1 0 2 C 3 .
So our final answer is 1 0 1 C 2 × 1 0 2 C 3 = 8 6 7 0 8 5 0 0 0