Parities kinda handy

$\dfrac{n(n+1)}{2}$

$\Rightarrow \dfrac{999(1000)}{2} = 499500 \longrightarrow \text{Even}$

Hence the answer is $\color{#D61F06} \boxed{\text{false}}$

Didn't see a solution using modulo calculations, so here we go: $if\ n \equiv 1, 2 \mod 4\ then \ the \ sum \ is\ odd.$ $if n\ \equiv 3, 4 \mod 4\ then\ the\ sum\ is \ even.$

Since $999\equiv 3 \mod 4$ , the sum is even.

using the formula, $\frac{n(n+1)}{2}$ for that ,

$\frac{999(999+1)}{2}=\frac{999000}{2}$ .............[clearly seen that it is divisible by 2,so it is an even number]

note:Any integer that can be divided exactly by 2 is an even number.and if the last digit of any integer is $0,2,4,6,8$ ,it s divisible by 2.

Extend the sum from 1 to 1000. Then there will be five hundred even numbers and five hundred odd numbers in the sum.

Just a little thought shows that since there are an EVEN number of ODD numbers in this sum the total will be EVEN. (Because the odd numbers can be summed two at a time to give even numbers. Adding these with the even numbers in the sum produces an even number).

Taking away 1000 (an even number) from the extended sum does not change the parity, and so

1+2+3+.........999 is EVEN.

1 + 999 even, 2 + 998 even, 3 + 997 even, ... It cancels out and becomes even. Therefore false

we know that from 1 to 1000 there are 500 odd, 500 even.

The sum of $k$ odd numbers is even iff k is even.

so $1 + 2 + 3 + \dots + 1000 - 1000$ is even

Every group of four goes odd,odd,even,even. $\frac{999}{4}$ is 249 with a remainder of three so those three will be odd,odd,even. The last one is even.

Find the sum to 999 and then check it:

$\large \color{#3D99F6} \frac{n(n+1)}{2} \color{#20A900} \implies \frac{(999)(1000)}{2} \to \frac{999000}{2} = \color{magenta}499500 \color{#EC7300} \implies \text{which is Even}$

$\boxed{odd}+\boxed{odd}=\boxed{even}$

$\boxed{odd}+\boxed{even}=\boxed{odd}$

$\boxed{even}+\boxed{even}=\boxed{even}$

In other words the addition of an odd number to the sequence will flip the result, and the addition of an even number will leave it untouched. We start with an odd number, and the sequence of additions will always be:

$\boxed{odd}+\boxed{even}+\boxed{odd}+\boxed{even}....$

We can confirm then, that the sequence of the sums will start as odd, then it will stay like that, then it will switch to even and stay once more before repeating, or in other words, it will always be

$\boxed{odd},\boxed{odd},\boxed{even},\boxed{even}$

Since the pattern repeats and has a length of 4, we know adding up to a multiple of four, and one less than, will always result in even sums, and adding up to anything else will always result in odd sums, so all we need is the modulo 4 (remainder when divided by 4) of the last number we're adding.

$999\equiv 3 \pmod{4}$

Or in other words, 999 is one less than a multiple of 4, so the sum of all integers up to 999 must be even.

There is a pretty clear pattern here. Each time a new odd number in the sequence is added, the sum changes between odd and even, so we can work out whether the sum will be odd or even without computing the sum.

1 is odd, 1+2+3 is even and 1+...+5 will be odd. This pattern will repeat all through the sum.

To determine if $\displaystyle \sum_{i=1}^{x} x \text{ is odd or even, where } x \text{ is odd and } x>1 \text{, simply find } \frac{x-1}{4}. \\$

$\text{If n is any integer and } \displaystyle \frac{x-1}{4} = \begin{cases} n & \quad \text{ the sum is odd } \\ n+0.5 & \quad \text{the sum is even} \end{cases}$

In this case, $\displaystyle \frac{x-1}{4} = \displaystyle \frac{998}{4} = 249.5 = 249 + 0.5.$ Therefore, $\displaystyle \sum_{i=1}^{x} 999$ is even.

1+999=1000 (even) + 2+998=1000 (even) + 3+997=1000 (even)...+ 499+501=1000 (even), + 500 (also even) = even Steven.

To solve it quickly try to make the question more simpler

When you need to do it quick follow this method

   Prerequisite information ;-

The logic uses 2 notions:-

• EVEN NUMBERS :- 

                     ✓  Sum of even numbers is always even


  • ODD NUMBERS :-

                     ✓ sum of odd number(s) of odd number(s)  is always  odd


                    Example:-   1+3+5=9
                                         1+3+5+7+9=25

                    ✓sum of even number(s) of odd number(s) is always even


                  Example :-.      1+3=4
                                             1+3+5+7= 16

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, Proof.

Sum of first n odd numbers results in n^2. Or in words n squared. Or n*n So we can conclude

• if n is even the sum is even

[square of even number is always even and is also divisible by 4 ]

-if n is odd the sum is odd

[ Square of odd number is always odd. , It is divisible by neither 2 nor 4 ]

For more eloboration comment on your doubts.
......... Alternative ......... Let a b c be 3 odd numbers. And the be equal to (z+1) (y+1) (x+1). respectively

So , z,x ,y are even as a number before a odd number is even

For odd number of terms

z+1+y+x+1+1 =. Even number +3= odd number

For even number of terms

z+y+1+1= even number+ 2 = even number

This can be followed for any number of terms

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

Now

1+2+3+4+5+6+7+8+9.................................+997+998+999

=(1+3+5+7.......................................997+999)+(2+4+6+8+10..................+998)

=( 1+3+5+7...............+999)+ a even number

Here there are 500 odd numbers So, its clear that their sum would be even

= even number +even number =even number

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

Most of you may comment its to lengthy

      But I just solved it in 5 seconds after reading the question (approximated)

I only calculated the whole in mind only. I am honest, but i could have solved it even quickly. I was not focused and lacked proper conditions for it.

Its just a matter of pre requisites that has taken all this space

,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,

                      ( Or)

You can use one of the formulae taught to you in middle school (mostly)

∆ Sum of cosecutive numbers = ( n/2)*(first term +last term)

where n is the total number of terms to be added

Here,

(999/2) (1+999) = 1000 (999/2) =999000/2. = 499500

............................................................

Most of you may comment its to lengthy

      But I just solved it in 5 seconds after reading the question (approximated)

I only calculated the whole in mind only. I am honest, but i could have solved it even quickly. I was not focused and lacked proper conditions for it.

  Its just a matter of pre requisites that has taken all this space


           My theories had to be more clearly conveyed  so I had to eloborate it so all readers can understand it and get benifited

............................................................

  My aim was to help others not only to solve but also to think differently and quickly. That would improve thinking by  one's self rather than following all ideas of others


        Please value my work and time for your benifit UPVOTE THIS SOLUTION and FOLLOW ME if you're interested to do so 

    The whole and sole purpose of this was to help others

The odd/even solution is cyclic in groups of 4, odd, odd, even, even, therefore we can divide by 4 and consider only the remainder (mod 4). 996 is the highest multiple of 4 that is lower than 999, therefore 999 is the 3rd number in the next odd, odd, even, even sequence. 997 odd, 998 odd, 999 even , 1000 even. So the correct answer is false.

I know the formula that Munem Sahariar posted below and that is a great approach to the problem, but I wanted to see if I could do it a different way. I realized that there are 1000 numbers from 1 to 999. I matched 1 with 999, 2 with 998 and so on, knowing I would get 500 pairs and each pair added up to an even number. Not elegant but pretty simple.

Call $S_n$ as the sum of $n$ natural numbers. Then, $\begin{aligned} S_n & = 1+2+3+\cdots + n \\& S_n = \displaystyle\sum_{n=1}^{n} = \dfrac{n(n+1)}{2}\end{aligned}$ let's make some observations to determine the obtained number from sum is either $\text{odd}$ or $\text{even}$

Case 1 : If $\frac{n}{2} = p\in\mathbb Z^{+}$ and $p$ is an odd integer, then there exist $\frac{p-1}{2}$ even terms/ $\frac{p-1}{2}$ odd paired terms and one remaining odd number which implies that obtained integer will be $\text{odd}$ .

For example:

$\begin{aligned} S_6 & =\boxed{1+2}+\boxed{3+4}+\boxed{5+6} \\& =\boxed{odd}+\boxed{odd}+\boxed{odd} \\& = \boxed{even}+\boxed{odd}\\& = \boxed{odd}\end{aligned}$

Case 2 : If $\frac{n}{2} = q\in\mathbb Z^{+}$ and $q$ is even integer, then there exists always $\frac{q}{2}$ even terms which shows that number obtained will be always $\text{even}$ .

For example :

$\begin{aligned}S_4 & = \boxed{1+2}+\boxed{3+4} \\& = \boxed{odd}+\boxed{odd}\\& = \boxed{even}\end{aligned}$ .

Case 3: If $\frac{n}{2} \in\mathbb Q^{+}$ or is rational number, then $\frac{n+1}{2}$ should be noted to determine whether the number is odd or even.

If $\frac{n+1}{2}$ is odd, then the number will be $\text{odd}$ .

If $\frac{n+1}{2}$ is even, then the number will be $\text{even}$ .

$S_{999}$ is the third case in which $\frac{n}{2}$ is rational number and when noting $\frac{n+1}{2} = \frac{1000}{2} =500$ is even number, Therefore the answer is $\text{even}$ .

$\displaystyle\sum_{i=1}^{999} i = 499,500 \longrightarrow \color{#20A900} \boxed{\text{Even}}$

There are 500 odd numbers and 499 even numbers where total numbers are 999.

even + even = even (always).so the summation of 499 even numbers makes a 'even number'.

Again, odd + odd+..(even times)=even odd+odd+odd+..(odd times)=odd so,the summation of 500 odd numbers makes a 'even number'.

And the last two even numbers make a even number.

Ans:False

I searched a rule (formula) for the general problem: when

$1 + 2 + \ldots + n$

is even or odd ?

I found that, if

$S_n:=\displaystyle \sum^n_{i=1}i$

is the sum, then, setting

$k:=(n+1)\setminus2$

(where " $\setminus$ " stays for the quotient operator), we have that

$S_n \equiv k \pmod{2}$

Proof. Given $k$ as defined, it can be easily found that:

$n = \begin{cases} 2k-1, & k=1, 2, \dots \\ 2k, & k=1, 2, \dots \end{cases}$

alternatively for odd and even $n$ .

We know that:

$S_n=\frac {n(n+1)}{2}$

so we can write (note: $"\%"$ stands for the remainder operator):

$S_n\%2=(\frac {n^2+n}{2})\%2= \begin{cases} (\frac {4k^2-4k+1+2k-1}{2})\%2, & n \verb+ odd+, \\ (\frac {4k^2-2k}{2})\%2, & n \verb+ even+. \end{cases} =\begin{cases} (2k^2-k)\%2, & n \verb+ odd+, \\ (2k^2-k)\%2, & n \verb+ even+. \end{cases}$

Thus always:

$S_n\%2=(2k^2-k)\%2 =-k\%2=k\%2$

as the thesis.

In this way, for $n=999$ , $k=500$ , hence $S_{999}$ is even.

Is 1 + 2 + 3 + ... + 998 + 999 an odd number ? No. Here is why :

By definition, with n, m, k integers in the following :

• The parity is the quality of a integer, being either 'odd' or 'even'. Lets note p(n) the parity of n.
• p(2n+1) is 'odd' (1)
• p(2n) is 'even' (2).

Let's prove that p(k + 2n) = p(k), or said simply, you don't change parity of any number by adding an even number to it. let's consider the cases where k is odd then even : if k is odd then k = 2m+1 with m an integer. 2m+1 + 2n = 2(n+m) + 1 and 2(n+m) + 1 is therefore also odd because (n+m) is an integer. if k is even, k = 2m and 2m + 2n = 2(n+m) and (2(n+m) is also even. The parity does not change in either case.

• p(k) = p(k + 2n) (3)

Similarly, let's prove the parity of the sum of two odd numbers to be even : (2n + 1) + (2m + 1) = 2(m+n+1)

• 4) $p( n_{odd} + m_{odd}) = 'even'$

4 consecutive integers following any k are k+1, k+2, k+3, k+4. The sum of these is 4k + (1 + 2 + 3 + 4) = 4k + 10 = 2 (2k+5) and 2n+5 is an integer, so :

• The sum of four consecutive integers is always even. (5)

From and (3) and (5) it results that subtracting any 4 consecutive integers from a sum does not change it's parity.

The sum $p(\sum\limits_{i=1}^{999} i$ can be written as a certain number of these packets of four, plus the remaining terms completing the list up to 999. Let n be the number of packets as defined above that we can subtract from the sum without changing its parity.

$\sum\limits_{n=1}^k (4n+1 + 4n+2 + 4n+3 + 4n+4)$ will always have an even parity.

$4k + 4 ≤ 999$ $4 ( k + 1) ≤ 999$ $k + 1 ≤ \frac{999}{4}$ $k ≤ \frac{999}{4} - 1$ $k ≤ 248$ maximum k is 248 4k+4 = 996

Therefore the parity of the whole sum is the same as : $p(\sum\limits_{i=1}^{999} i = p(997 + 998 + 999)$ $= p(998) by (4)$

and so the sum 1 + 2 + 3 + ... + 999 is even and not odd, the result is false.

1+2+3+.......+998+999

+

999+998+997.....+2+1 =1000+1000+........+1000+1000

There are 999 thousands. So, [999×1000]÷2 gives the sum of the given series which is even. So the statement is false.

The sum of 1 + .... + n = n(n+1)/2. The numerator factors are always one odd and one even number. For the sum to be even it is necessary for the even factor to also be divisible by 4 in order for the sum to be even after dividing by the denominator 2.

The sum is even if and only if either n or n + 1 is divisible by 4.

In this case n = 999, n + 1 = 1000 = 4 x 250, therefore the sum is even, and the statement is false.

Every 3rd and 4th number added will have an even sum. 1000 is divisible by four and 999 is the number before it so they must have an even sum.

That’s quite an interesting pattern! Analyzing this sequence of triangular numbers (Just 1, 1+2=3, 1+2+3=6, ...), we get an infinite cycle of O, O, E, E, O, O, E, E, ... (O=Odd and E=Even)! This cycle loops every 4 integers, and the largest multiple of 4 less than 999 is 996. 999-996=3, meaning the third member of this infinite loop, an even number! Thus 1+2+3+...999 is even, not odd!

Since 1+2+3+4+5...+999 has a total number of terms of 999, we can split the terms into halves, even if they won't be equal, and have every opposing sides of the equation added as a pairs (1+999= 1000, 2+998= 1000, 3+997=1000, ...). Based on this number theory, if 499 of the terms each equals to 1000, that last unpaired term should be half of the the two pairs equal to 1000 we've listed off so far, so that would be (499*1000)+ $\frac{1000}{2}$ = 499500, which is an even number. Therefore, the answer for this question would be false.

Simplistic view with no written calc. It goes 1 Odd, 2 odd, 3 even, 4 even then repeats. 1000 is divisible by 4, so is even. 999 is 1 back in the pattern so is even.

if the the sum of the first and the last number of the progression divided by 2 is even the sum is even. In this case (1+999)/2 = 500 is even. (The result is odd only when the the first and the last number of the progression divided by 2 is odd AND the number of progression members is ODD)

n = odd

1 + n = odd

1 + 2 + n = even

1 + 2 + 3 + n = even

1 + 2 + 3 + ... + n = odd ?

n mod 4 = b

if b = 1 or 2 then n = odd

if b = 3 or 0 then n = even

999 mod 4 = 3

then 999 is even , so the answer is false .

The pattern follows as two odd then two even. Every second number is even, duh, but every second number is also the last of the even or odd kind. e.g. 1+2, 2 is even and 1+2 is odd. If 2 is divided by 2 we get an odd number (1). If 4 is dived by 2 we get an even number. The pattern follows. So when we get to 999 we now that this must be the first number that is in either the even or odd series so we add 1 to get the second number which we divided by 2 to find if it is even or not and we end up with 500, which even; thus 1+2+3+...+999 is NOT an odd number, making the answer false. Or you could use the smart formula of $\frac{n(n+1)}{2}$

The Sum of an arithmetic series is written by the formula Sn = n/2{2a+(n-1)xd} In this case, a=1, n=999 and d=1 therefore 999/2[2(1)+(999-1)x1] = 999/2(1000) = 499500 Therefore as this is an even number the answer is false

Parity switches on the odds; f (1) is odd, f(2) is odd, f(3) is even, f(4) is even, f(5) is odd , f(6) is odd, f(7) is even. It'll just cycle like that. So numbers of the form 4n+1 and 4n+2 result in odds and the rest result in evens.

$1+2+3+4+.....999=\dfrac{999(1000)}{2}$ $\Rightarrow \dfrac{999(1000)}{2} = 499500 \longrightarrow \text{Even}$ Hence the answer is $\color{#20A900} \boxed{\text{False}}$

odd + even = odd

odd + odd = even

even + even = even

Therefore:

1, 1+2=3, 3+3=6, 6+4=10, 10+5=15, 15+6=21, 21+7=28, 28+8=36, 36+9=45, 45+10=55, 55+11=66, 66+12=78

odd, odd, even, even, odd, odd, even, even, odd, odd, even, even

999/4 = 249 + 3/4 (odd,odd,even,even)+...+(odd,odd,even,)

1+2+3+...+999 Is Even

$1 + 2 + 3 + ... + 997 + 998 + 999 = a$ Notice that: $1 + 999 = 1000$ and $2 + 998 = 1000$ and $3 + 997 = 1000$ so $(1 + 999) + (2 + 998) + ... = a$ which is the same as saying $1000 + 1000 + ... = a$ At first we were adding 999 terms one by one, and now we're adding the terms two at a time, which means wee are now adding half of the original number of terms so we can write that as $\frac {999}{2} * 1000 = 999 * 500 = a$ which is even. If you liked this answer thank the young Johann Friedrich Carl Gauss for this method.

Here is a pattern:

It does not matter how many even numbers there are, because the sum of n even numbers is always even.

But it does matter how many odd numbers are, because the sum of n odd numbers is:

a) Odd, if n is an odd number

b) Even, if n is an even number

Assuming that between 1 and 999 there are 500 odd numbers, and 500 is an even number, the statement is false.

it is a reapeating sequence of five. The first odd number of the the sequence is 1,5,10,15,... then 1000 will be the first odd number of a sequence , then 999 ( the previous number) is even

Let S(n) equal the sum from 1 through n. Extend the sums until you see the pattern emerge: S(1)- Odd; S(2)- Odd; S(3)- Even; S(4)- Even; S(5)- Odd; S(6)- Odd; S(7)- Even; S(8)- Even; S(9)- Odd.

This should be enough to see that the pattern repeats in groups of 4: Odd, Odd, Even, Even. Every number that is divisible by 4 ends the group, and the sum to that point is always Even. Every number just before the multiple of 4 is also Even. 1000 is divisible by 4, so S(1000) is Even. 999 is the one just before it, so S(999) is also Even.

We notice from the first few levels a pattern of periodicity 4. 1 level plus 250 periods puts us at an end term of 1001, with the same pattern placement (odd, next being odd). Taking two steps back to an end term of 999 puts us at a pattern placement of even

Sum of first n integers = n(n+1)/2

Hence, the sum =999×1000/2

=999×250×2

a multiple of 2

The series has an even number of odd integers (500), so it must be even.

Since the sequence is defined by the sum of the previous result with the current sequence term, it satisfies the following statement:

$a = r + n$

Where:

$a = total$

$r = result$

$n = term$

In which it can be also written as:

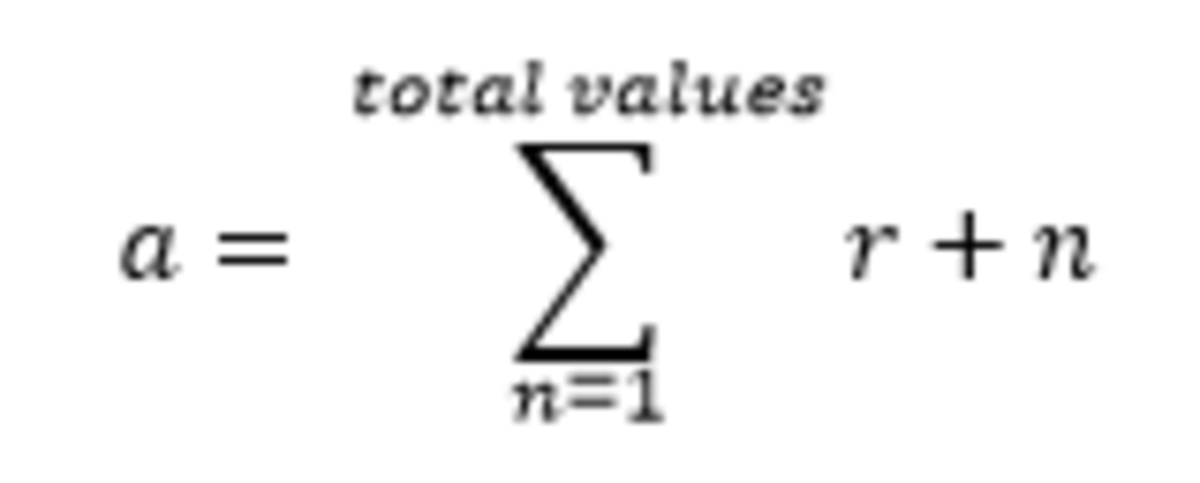
So the answer would be:

Therefore $1+2+3…+999$ is not an odd number

Ans.: FALSE

$1$ is an $\color{#D61F06}\text{odd}$ number.

$1+2$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3$ is an $\color{#3D99F6}\text{even}$ number.

$1+2+3+4$ is an $\color{#3D99F6}\text{even}$ number.

$\ldots\ldots\ldots$

$1+2+3+4+5$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6+7$ is an $\color{#3D99F6}\text{even}$ number.

$1+2+3+4+5+6+7+8$ is an $\color{#3D99F6}\text{even}$ number.

$\ldots\ldots\ldots$

$1+2+3+4+5+6+7+8+9$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6+7+8+9+10$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6+7+8+9+10+11$ is an $\color{#3D99F6}\text{even}$ number.

$1+2+3+4+5+6+7+8+9+10+11+12$ is an $\color{#3D99F6}\text{even}$ number.

$\ldots\ldots\ldots$

$1+2+3+4+5+6+7+8+9+10+11+12+13$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6+7+8+9+10+11+12+13+14$ is an $\color{#D61F06}\text{odd}$ number.

$1+2+3+4+5+6+7+8+9+10+11+12+13+14+15$ is an $\color{#3D99F6}\text{even}$ number.

$\ldots\ldots\ldots$

therefore, for line ending 999 $\pmod{4}$ = 3

therefore, from third line above is $\color{#3D99F6}\text{even}$ therefore $\color{#D61F06} \boxed{\text{false}}$

I just guessed :(

We know that $S_n = 1+2+3+\cdots+n = \dfrac {n(n+1)}2$ and that either $n$ or $n+1$ is even and the other odd. For $S_n$ to be even the even $n$ or $n+1$ must be a multiple of 4. Since $1000$ is a multiple of 4, $S_n$ is even Therefore, the answer is false .

Generalization: For $S_n$ to be even, either $n$ or $n+1$ must be a multiple of 4. Otherwise it is odd.

999 is odd and (999+1)=1000 is even, further 1000/2=500 is even. Therefore, 1+2+3+....+999 is an Even number

In general, in the sum of first n natural number:

Either one of the value n or (n+1) is even, further divided the even number by 2 and if the result is even the sum of the series is even otherwise sum of series is odd.