Parliament
Among 30 people, any two are either mutual friends or enemies, and each person has exactly 6 enemies. How many groups of three people consist of all pairwise friends or all pairwise enemies?
The answer is 1990.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Shouldn't you also show that this arrangement of friends/opponents is actually possible? It is, but...
Log in to reply
Here is a group of ten people each of whom are enemies with exactly six of the others (only the lines of enmity are marked). Have three disjoint graphs like this.
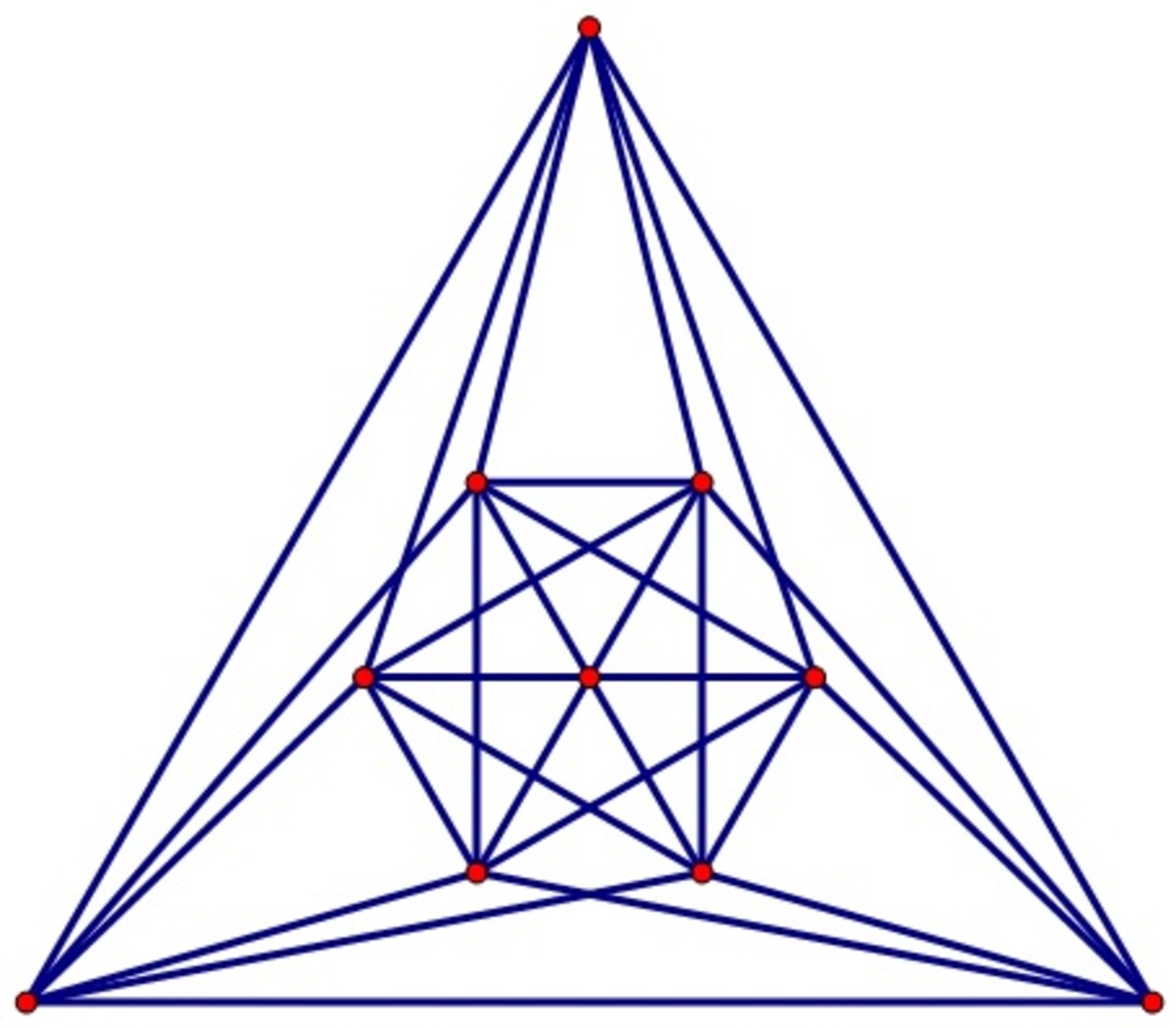
Log in to reply
Great example! What led you to derive this graph?
Log in to reply
@A Former Brilliant Member – I was looking for an example, and thought it would be easier to find if the graph could be split into disjoint subgraphs. I therefore tried to find examples for n people, where n was a factor of 3 0 . Since n > 6 , n = 1 0 was my first attempt!
Log in to reply
@Mark Hennings – An easy example is to index everyone from 1 to 30, and then you are enemies with people ± 1 , ± 2 , ± 3 (taken modulo 30).
i don't know, what is bad angles ? as well as what is good triangle ? why do you use good and bad ?
Log in to reply
I defined a bad angle as an angle with sides of different colours. I defined a good triangle as a monochromatic triangle. Hence, a bad triangle means a triangle which is not a good triangle . I used these definitions (good and bad) so that my solution is easier to follow and not so wordy (which would be the case if I had to use the lengthy definition every time).
Great job on the graph. Nice problem too =)
Let us represent 30 persons with 30 points in space, no four points of which are coplanar. If two persons are friends that connect the corresponding points with a red segment and a blue segment if they are opponents. We denote an angle that has sides of different colours as a bad angle . Observe that in a good triangle there are no bad angles and in a non-good/bad triangle , there are 2 bad angles . Now, from the question, we can deduce that the number of bad angles per person is 2 3 × 6 = 1 3 8 and 1 3 8 × 3 0 = 4 1 4 0 for the entire parliament. Since two bad angles are needed for each bad triangle , we have 4 1 4 0 ÷ 2 = 2 0 7 0 bad triangles . Given that the total number of triangles within these 30 people is 3 0 C 3 , the answer is therefore 3 0 C 3 − 2 0 7 0 = 1 9 9 0 .