Particle Leads Parabolic Track
A particle having charge ( − 2 0 2 0 C ) and mass 2 0 2 1 k g moves in x − y plane. A constant electric field E = 2 N C − 1 is present in the region along positive y direction. The equation of motion of the particle has form y = 3 x − 4 x 2 . Find the speed of the particle at the origin. If your answer comes in the form of 1 4 . 5 9 ,then type it as 1 5 (round off to nearest integer)
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase I was getting 1 . 9 9 9
Did you get 0.5 for the horizontal speed?
Log in to reply
I get v x = 2 q a where a = − y ¨
Log in to reply
@Steven Chase Btw how to write that double derivative in dot form. I just get tired by finding that sign in latex.???
Log in to reply
@A Former Brilliant Member – Just add another d in the latex. \ddot{x}
Where does that expression come from?
Log in to reply
@Steven Chase – @Steven Chase Did you find out any mistake. Link?
Log in to reply
@A Former Brilliant Member – What link?
Log in to reply
@Steven Chase – @Steven Chase Check your notifications
Log in to reply
@A Former Brilliant Member – I don't see a link anywhere
@Steven Chase
I wanted to show this through that link. Now forget that link.
I am also little comfused in this question. The solution of this question which I get on the web few days ago is this

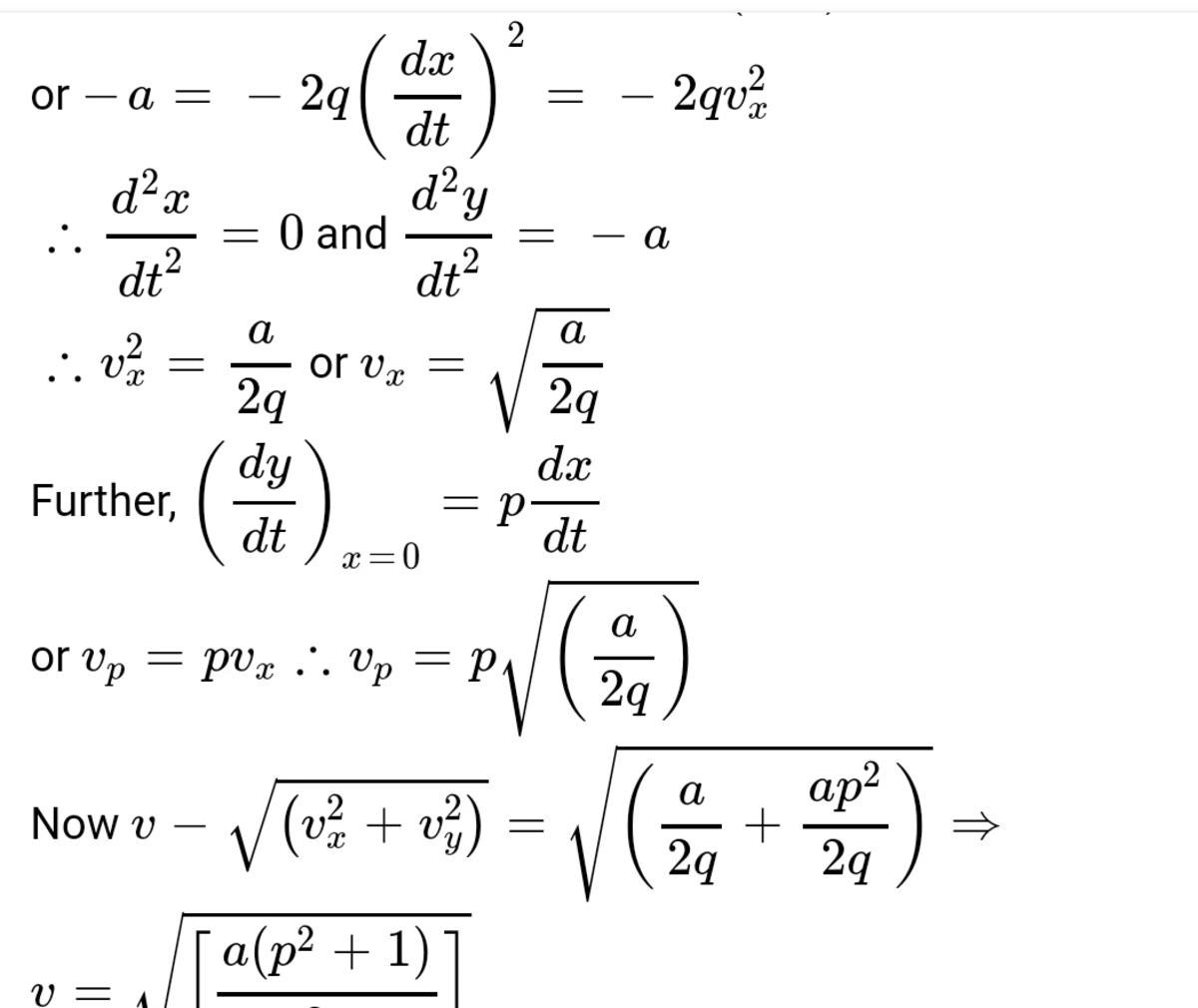
Log in to reply
The first line of the solution is obviously wrong
Log in to reply
@Steven Chase – @Steven Chase well this solution is provided ny a website which is wrong and I have attached answer according to this only.as therefore I was also little bit confused.differentiating with respect to x in left . And differentiating with respect to t in right. Yes I also faced this problems.i will correct the problem according to your answer. Cheers!!
Log in to reply
@A Former Brilliant Member – Sounds good, thanks
Log in to reply
@Steven Chase – @Steven Chase will you make a problem on M a g n e t i s m which is entirely new. By doing these flux problem I am getting bored Now I want to do NEW problems.
Let the horizontal and the vertical components of the velocity of the particle at the origin be u and v respectively. There is no acceleration in the horizontal direction, and hence u is constant. Acceleration of the particle along the downward vertical direction is w = 2 0 2 1 2 0 2 0 × 2 m/s 2 . Hence the equation of the trajectory of the particle is y = u v x − 2 1 w u 2 x 2 . Comparing with the given equation, we get v = 3 u , u 2 = 8 × 2 0 2 1 2 0 2 0 × 2 ⟹ the magnitude of velocity at the origin = u 2 + v 2 = u 1 0 = 2 0 2 1 5 0 5 0 ≈ 1 . 5 8 . So the answer is [ 1 . 5 8 ] = 2 .
Assume that the electric force is solely responsible for the trajectory. The position, velocity, and acceleration are:
x = x y = 3 x − 4 x 2 x ˙ = x ˙ y ˙ = 3 x ˙ − 8 x x ˙ x ¨ = x ¨ y ¨ = 3 x ¨ − 8 ( x x ¨ + x ˙ 2 )
At x = 0 :
x ¨ = x ¨ y ¨ = 3 x ¨ − 8 x ˙ 2
We know that the electric field is only in the y direction, so this further reduces to:
x ¨ = 0 y ¨ = − 8 x ˙ 2
Setting the force equal to the y acceleration:
m a = q E 2 0 2 1 ( 8 x ˙ 2 ) = 2 0 2 0 ( 2 )
This yields:
∣ x ˙ ∣ ≈ 0 . 5 ∣ y ˙ ∣ ≈ 1 . 5 x ˙ 2 + y ˙ 2 ≈ 1 . 5 8