Particular Pentagon Point
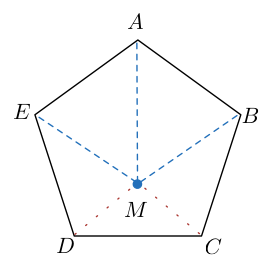 The point
M
lies inside regular pentagon
A
B
C
D
E
such that
∠
M
B
A
=
∠
M
E
A
=
4
2
∘
. Find
∠
D
M
C
.
The point
M
lies inside regular pentagon
A
B
C
D
E
such that
∠
M
B
A
=
∠
M
E
A
=
4
2
∘
. Find
∠
D
M
C
.
The above image is not drawn to scale.
A
B
M
E
need not be a parallelogram.
B
M
D
and
E
M
C
need not be straight lines.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This was how I did the problem, but showing that DM was 1 reduced to the identity sin ( 5 4 ) = 2 cos ( 6 6 ) sin ( 8 4 ) (in degrees), which isn't immediately obvious to me.
Log in to reply
It was not obvious to me, either. I put it into my calculator and was a little bit surprised. Perhaps it could be a proof for my Pre-Calculus class, using anlge sum formulas...
How do you use law of sines to find EM?
Log in to reply
If this is a regular pentagon, then it is obvious ∠ B A E = 1 0 8 ∘ , therefore ∠ B M E = 1 6 8 ∘ . By using symmetry, ∠ A M E = 8 4 ∘ and ∠ M A E = 5 2 ∘ . Since we know all the angles of Δ AME and A E = 1 , calculating E M can be done by using law of sine.
Log in to reply
How you get angle MAE =52
??
Bingo
it have more than one ans
Drawing a sketch, you might suspect that the desired angle measure is 60°. This happens to be correct, but how to prove it? We can do so by reasoning "backwards"--that is, begin with a point N inside the pentagon such that Δ D N C is an equilateral triangle, then show that N coincides with our point M .
Let N be such a point. Since the angles of Δ D N C are all 60°, both ∠ B C N and ∠ E D N measure 1 0 8 ∘ − 6 0 ∘ = 4 8 ∘ . Since the segments B C , C N , E D , and D N are all congruent, Δ B C N and Δ E D N are both isosceles. This allows us to find that ∠ C B N = ∠ D E N = 6 6 ∘ , and therefore ∠ N B A = ∠ N E A = 1 0 8 ∘ − 6 6 ∘ = 4 2 ∘ .
Since there is only one point inside the pentagon satisfying the given properties (forming the two 42° angles), the points M and N must coincide. (That claim may require more justification--feel free to provide it for me!) Therefore the desired angle is, indeed, 60°.
I have two doubts in this answer. Please clear them if you can.
-
how congruence of BC, CN, ED, DN implies that triangles BCN and EDN are isosceles?
-
If triangle BCN is isosceles, then angles EDN and END are both 48 degrees. That will imply angle CBN =180 - 2*48 = 84, which contradicts your result (angle CBN = 66) !
Log in to reply
A triangle is isosceles if two of its sides are congruent. But merely stating that a triangle is isosceles is only giving part of the story, since it is a claim that two of the triangle's sides are congruent without saying which two sides are the congruent ones. And that's an important piece of the puzzle!
The fact that B C = C N makes triangle BCN isosceles, so the angles of triangle BCN that are opposite those sides,namely BNC and CBN, must be congruent. So if ∠ B C N = 4 8 ∘ , and ∠ B N C ≅ ∠ C B N , then ∠ B N C = ∠ C B N = 2 1 ( 1 8 0 ∘ − 4 8 ∘ ) = 6 6 ∘ . A similar argument shows that the same is true for ∠ D E N .
I hope that was helpful.
Oh, I forgot to mention that I got this problem from Mathematical Olympiad Challenges by Andreescu & Gelca. (Highly recommended!)
Log in to reply
Hi, can you show a method where we can directly find the angle (without simply trying 6 0 o )
Log in to reply
Not at the moment, but I am working on it! You?
Log in to reply
@Matt Enlow
–
I dont know...It seems obvious that the angle must be
unique
, so it has to be solvable..
But, somehow there is an angle that is necessary to get the required angle (which I do not know)
Namely,
if I somehow get the angle
E
D
M
or
E
M
D
, then I will be done..(but, the equations do not work out as I expected it to)
I will try my best though to find it somehow..Thank you for response.
Can You tell me what I am doing wrong...??In triangle MBA...A is 54,B is 42 so M is 84...ditto for triangle MEA....Therefore EMB is 168...using vertically opposite angles...i got DMC is 168....
Log in to reply
Those angles are not vertical. They may appear so in the diagram, but the five segments coming from M are five separate segments.
Log in to reply
Though the five segments from M are seperate, by the logic of sommetry, AM should be angle bisector of angle EAB, so should be 54.
Log in to reply
@Sagar Kulkarni – Yes, I agree with that. I'd even agree that ∠ E M B = 1 6 8 ∘ .
Damn it...my mistake...sorry!!Thanks for making it clear!!
I got 48 for some reason.
This doesn't look correct. I can prove that MBA and MEA will be 42 even if DMC is not 60. I proved that DCM= BMC-6. But the exact value of DMC is unclear.
I just used a law of sines bash. Slow and sluggish, but it works.
but to try analyzing.. the illustration itself shows that the angle is more 90 degrees. below it is so numb
Hi guys, I did it by unconventional method and got the answer as 0 (zero). I would like to share the geometric shape along with the algebra. Can some one guide me how to share the picture. Hopefully someone will find flaw in my solution.
I think there is more than one solution to this problem.Please refer to my post and see if its right?
If I didn't know that the measure was 60º, could I still solve this without trig? If yes, how?
If we didn't assume the angle to be 60,, is there a way to solve this without using trig?
this is wrong solution i bet
abme is a parallelogram and sum of all sides of parallelogram is 360 by this u can easily measure angle bme as it is vertical to dmc
Log in to reply
We can't assume that angles BME and DMC are vertical. MA, MB, MC, MD, and ME are simply five segments having M as an endpoint.
I got DMC =180° Check where I am wrong..
EAB=108°, AEM=ABM=42° So EMB should be 168°.
Let DMC be x°. So MDC=MCD= (180-x)/2. EDC is 108° This gives EDM = 108 - (180-x)/2.
As AED=108° and AEM =48°, MED should be 66°.
So we get EMD=BMC= 180- {66 + [ 108- (180-x)/2]} =6 - (180-x)/2
Now, DME + EMB + BMC + CMD = 360° i.e. 2[6-(180-x)/2] + 168 + x = 360
Solving, we get x=180° i.e. M is the midpoint of DC. Where am I wrong?
60 is the wrong answer i bet correct answer is 138
Log in to reply
you r wrong dude....
how? show us the proof.
From the properties of a regulat pentagon: < EAB =108 and from symmetry <MAB=54. In addition <CBM=108-42=66. Consequently from the triangle MAB we get <AMB=84. Since in the triangle MAB:AB/MB =sin(84)/sin(54) and in the triangle CMB: BC/MB=sin(<CMB)/sin(180-66-<CMB). Therefore we get sin(84)/sin(54)=sin(<CMB)/sin(114-<CMB)=1.2293. By rearranging this expression we get that tan(<CMB)=1.2293 sin(114)/(1+1.2293 cos(114)). then <CMB=66. Since 2 <CMB+2 <BMA+<DMC=360. Then <DMC=360-168-132=60.
sir, u r correct
your solution is perfect....
abme is a parallelogram and sum of all sides of parallelogram is 360 by this u can easily measure angle bme as it is vertical to dmc
Looks incorrect. How did u get sin(84)/sin(54)=sin(<CMB)/sin(114-<CMB). Seems you are assuming BC=AB which is not given.
Let Angle DME=CMB=m Let AngleDMC=n then 2m+n=192. Let ED=a. Then DM=a/2 cosec n/2 Now In triangle DME DM=a/2 cosec n/2 & ED=a Angle DME=m & Angle DEM=66. Apply sin rule
DME and CMB are not equal .. bcoz its not stated that BD and EC are straight lines
since angle MBA= angle MEA , therefore MBAE is a rhombus , so angle MBA + angle EMB = 180 degrees , so angle EMB = angle DMC ( vertically opposite ) = 180 - 42 = 138 degrees
Log in to reply
NOTE that angle EMB and angle DMC are NOT vertically opposite!
Let side length of pentagon be 2 units for convenience.
R = 1/ Cos 54 d
H = Tan 54 d
r = 2 Sin 42 d/ Sin 84 d
h = R + H - r = Tan 54 d + Sec 54 d - 2 Sin 42 d/ Sin 84 d = Sqrt (3)
Tan (x/ 2) = 1/ h = 1/ Sqrt (3)
x = 2 Atan [1/ Sqrt(3)] = 60 degrees.
In this question, only manipulation of angles could not give the answer wanted. I think 42 degrees for 60 degrees is a made figure since our logic tells that only whole numbers will be there. Not obvious and answer in a minute made me incorrect. Unless we knew this, I think an honest man won't be able to answer in a minute.
Matt, We let the side of the pentagon equal 1, then used law of sines to find EM. After we had EM, we used the law of cosines to find DM. It turned out that DM=1. This, by symmetry of the figure, meant that CM was 1, which makes the triangle DCM equilateral. Thanks for sharing this great problem and great website. Jeff (PROMYS 2002-2009)