Path Counting
Compute the number of paths from S (start) to G (goal) in the following image, without using any road twice (but may visit an intersection twice). As an explicit example, the path in pink is one valid path.
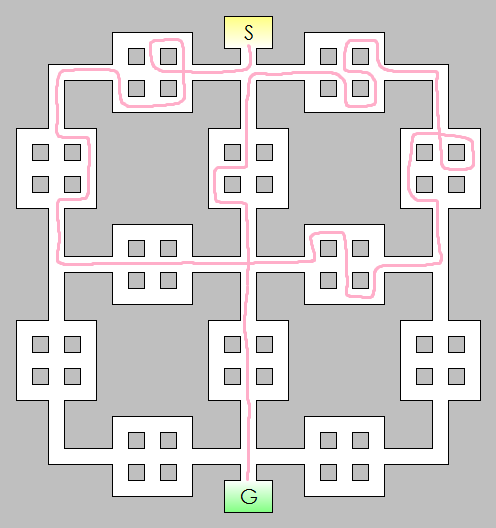
Clarifications:
- A road is a segment between two intersections that doesn't include any other intersection. A path is a connected sequence of roads from start to goal.
The answer is 16596325314442475.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
@Sunny Patel , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.
The big 2x2 grid is the same as each of the small grids on each of the edges, and the entrance and exit are at the same places, so they are, in a sense, the same problem --- if there are n ways through any 2x2 grid, then each length- k big path through the big 2x2 grid yields n k actual paths.
So... just DFS a simple 2x2 grid once naively and keep track of the path lengths. There are so few that we needn't bother putting them in a map or anything.
I'm too lazy to write purely functional code today. Destructive impure Scala code follows. It turns out that the answer fits in a Long, but since we can't easily figure that out without actually doing the problem, we use BigInt.
import scala.collection.mutable.ArrayBuffer
var go = Array.fill(9, 9)(false)
def setEdge(a: Int, b: Int, r: Boolean) {
go(a)(b) = r
go(b)(a) = r
}
for (i <- 0 until 3; j <- 0 until 2) {
setEdge(3*i+j, 3*i+j+1, true)
setEdge(3*j+i, 3*j+3+i, true)
}
var paths: ArrayBuffer[Int] = ArrayBuffer()
def dfs(cur: Int, depth: Int) {
if (cur == 7) paths += depth
for (i <- 0 until 9 filter go(cur)) {
setEdge(cur, i, false)
dfs(i, depth + 1)
setEdge(cur, i, true)
}
}
dfs(1, 0)
println(paths.map(BigInt(paths.length).pow).sum)
Nice!
Since your program counted the number of paths of each length, could you post the breakdown? I'm just curious.
P.S. Never mind, I've worked it out: 1,6,2,18,8. (Turns out that the problem is doable by hand -- I didn't try at first because I thought it would be far too complicated.)
It is 1,6,2,20,6.
The problem with computing by hand is that large number of 8-unit paths; at first I was also afraid I miscounted (missed/double counted some paths). Assuming you have the patience to carefully do all the paths by hand and you have a calculator with suitably large precision, you can do the rest by hand.
It is 1,6,2,20,6.
Thanks. I should have checked that more carefully.
Of course, the final answer can also be written as
6 K 2 6 1 1 2 2 5
where K is the digit representing 2 0 .
Of course, the final answer can also be written as 6 K 2 6 1 1 2 2 5 where K is the digit representing 2 0 .
Oh dear, another careless mistake on my part. That should have said 6 K 2 6 1 0 1 2 2 5
Python code:
def list_setup() :
l = [
[0,0,0,0,0,0,0],
[0,0,1,0,1,0,0],
[0,1,0,1,0,1,0],
[0,0,1,0,1,0,0],
[0,1,0,1,0,1,0],
[0,0,1,0,1,0,0],
[0,0,0,0,0,0,0],
]
return l
def count_all(l, counts, row, col, goalrow, goalcol, steps_so_far) :
if row == goalrow and col == goalcol :
counts[steps_so_far] += 1
for step in [(-1,0),(0,-1),(1,0),(0,1)] :
if l[row + step[0]][col + step[1]] > 0 :
l[row + step[0]][col + step[1]] -= 1
count_all(l, counts, row + 2 * step[0], col + 2 * step[1], goalrow, goalcol, steps_so_far + 1)
l[row + step[0]][col + step[1]] += 1 #undo
def foo() :
l = list_setup()
counts = [0] * 15
print "Counting..."
count_all(l, counts, 1, 3, 5, 3, 0)
totalcount = sum(counts)
print "Individual counts:", counts
print "Total Count:", totalcount
answer = 0
for i in range(0,15) :
answer += (counts[i]) * (totalcount ** i)
print "Answer:", answer
foo()
You can count how many ways there are to pass through those little squares that have the same shape as the whole path. You can only pass through an even number of squares since every time you change your path to make it longer/shorter, it will increase/decrease by a multiple of 2, and the shortest path is 2 squares.
There is 1 way to pass through 2 squares, 6 ways to pass through 4 squares, 2 ways to pass through 6 squares, 20 ways to pass through 8 squares, and 6 ways to pass through 10 squares. (12 squares isn't possible, which can be shown with similar reasoning to the Königsberg bridge problem).
For each way to pass through n squares, there are 1 + 6 + 2 + 2 0 + 6 = 3 5 ---> 3 5 n ways to go through that path.
1 ⋅ 3 5 2 + 6 ⋅ 3 5 4 + 2 ⋅ 3 5 6 + 2 0 ⋅ 3 5 8 + 6 ⋅ 3 5 1 0 = 1 6 5 9 6 3 2 5 3 1 4 4 4 2 4 7 5
This solution didn't go over how to count, since you just need some organized counting method (like counting paths that go through 2 squares, then 4, etc. or using symmetry).
You can count how many ways there are to pass through those little squares that have the same shape as the whole path. You can only pass through an even number of squares since every time you change your path to make it longer/shorter, it will increase/decrease by a multiple of 2, and the shortest path is 2 squares. There is 1 way to pass through 2 squares, 6 ways to pass through 4 squares, 2 ways to pass through 6 squares, 20 ways to pass through 8 squares, and 6 ways to pass through 10 squares. (12 squares isn't possible, which can be shown with similar reasoning to the Königsberg bridge problem). For each way to pass through N squares , there are 1 +6 + 2+ 20 + 6 = ---> 35^n ways to go through that path ..
1.35^2 + 6.35^4 + 2.35^6 + 20.35^8 + 6.35^10 = 16596325314442475
friends ...here is a solution by conventional way (like the way ramanujan would have solved it i guess ) .....
1) total number of different ways that you can enter in to a box ( lets consider that four points part as box) and get exit are 35.
explanation for 35 :
let's consider ONLY first box and enter in to it (note: we can take any box because all boxes are symmetric) The different ways to get out from box are following
if u enter and take right side ( up side ), the different paths are 10 (u have to try all possible cases)
if u go straight, the paths are 15
if u go left side ( down side), paths are 10 (it will be same as right side due to symmetric design )
2) now if u see whole figure all 12 boxes carefully and its paths , u could find that it's same pattern as the each box has..so by considering the boxes as lines u could go from S to G with 35 different paths.
3) we need to find how many boxes we have to pass to reach S to G in each path.
4) if u calculate, u will find that out of total 35 paths : 20 paths with 8 boxes , 6 path with 4 boxes, 1 path with 2 boxes, 6 path with 10 boxes and 2 path with 6 boxes
5) for example let a path having two boxes in the way so the possible different ways out
= (35)(35)= 35^2
so the same you apply here for first case 20 paths with 8 boxes: assume the boxes are in cascade so to reach S to G in this case u have 20(35^8) paths.
6) similarly if u do for all and add all of them, u wil get the answer
20(35^8) + 6(35^4) + 1(35^2) + 6(35^10) + 2(35^6) = 16596325314442475