Patterns in circles
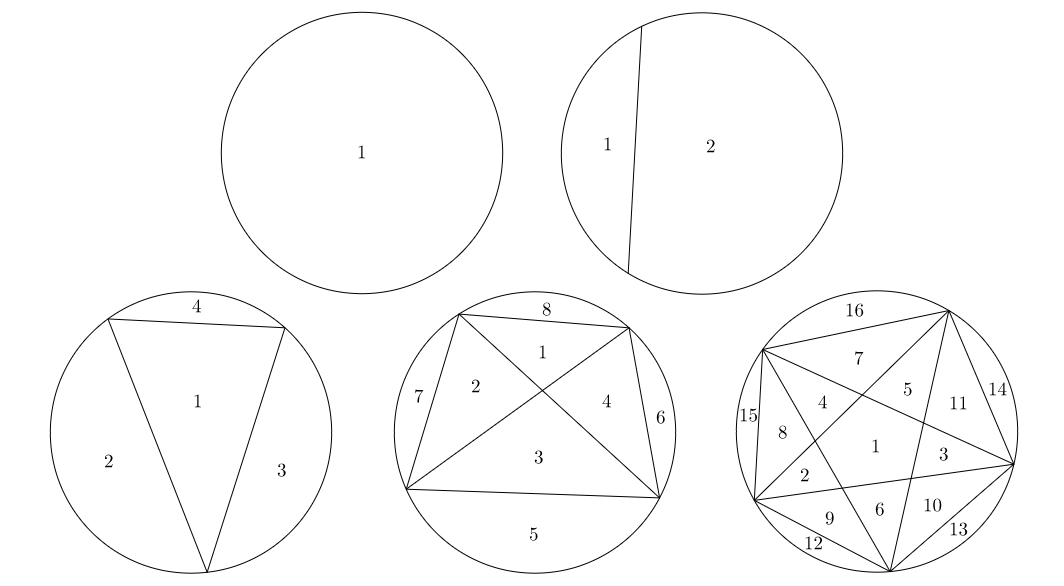
The above figure shows the number of regions that the interior of a circle can be divided into with the help of constructing all possible line segments with certain number of points on its circumference. For example, the first figure can be assumed to have one point on it's circumference (not shown in the figure), since we cannot draw any line segments so we have only one region which is that of the whole circle. Second figure has two points through which one can construct a unique line segment between them which will divide the circular region into 2 parts. The cases of 3,4 and 5 points are also shown in the diagram.
If we take six points on its circumference, then exactly into how many regions can we divide the interior of the circle?
Details:
The points should be chosen keeping in mind the following rules:
- Two or more than two points selected on the circumference of the circle should never coincide; otherwise they should be treated as a single point only.
- No three or more than three lines should have a common point of intersection inside the circle, i.e, taken any point in the interior of the circle (not the ones on the circumference of it) formed by the intersection of lines, only two lines should pass through it.
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 green next to them
12 brown at points, next to green
7 reddish brown in the center. (There would be only 6 in the center if the hexagon were regular, but the statement of the problem specifically excludes that possibility.)
Total: 6 + 6 + 1 2 + 7 = 3 1