Peacock Tail
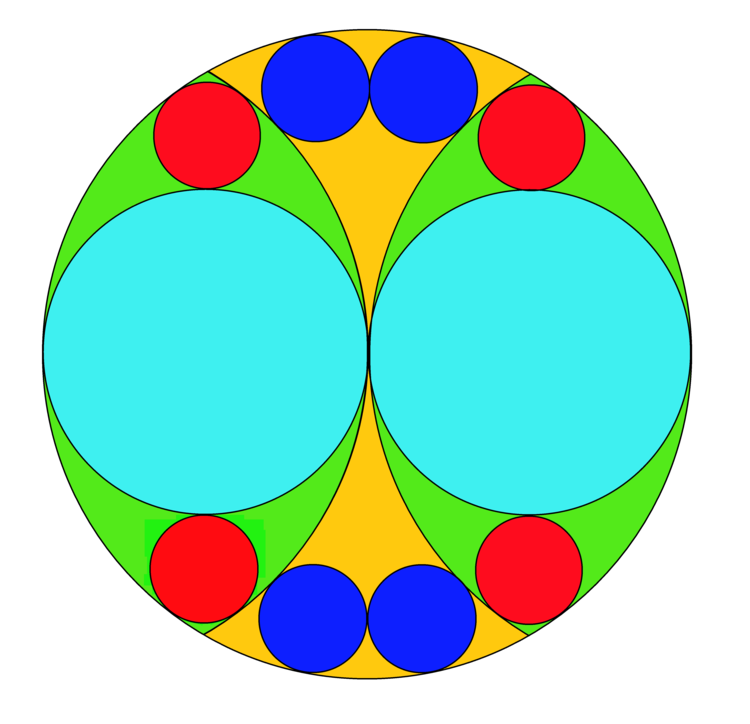In a circle of diameter 12, draw two tangent arcs of radius 6, and then 10 inscribed circles as shown; two of diameter 6, four red ones each of radius
a
and four dark blue ones each of radius
b
. Find
a
×
b
.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If r be the radius of the red (or blue) circles, then, (6-r)² = 3² + (3+r)² which yields, r=1.
That calculation works for the red circles, but it is not immediately obvious that the blue circles have the same radius. To show that they in fact do, we can proceed as follows. Form a triangle by joining the centers of the yellow, upper right) dark blue and (right) green circles and let the radius of the dark blue circle be r . This triangle will have side lengths of 6 , ( 6 − r ) and ( 6 + r ) . Divide this triangle into two right triangles by drawing an altitude from the center of the blue circle. These two right triangles then share this altitude as a common side, and so we can use Pythagoras to create the equation
( 6 − r ) 2 − r 2 = ( 6 + r ) 2 − ( 6 − r ) 2 ⟹ 3 6 − 1 2 r = 2 4 r ⟹ r = 1 .
@Banti Paswan Nice problem, (and a beautiful diagram, too). It would have almost been better if you had asked for the sum of the radii of the red and blue circles, since although they both have radius 1 , it takes separate calculations to determine their radii. The fact that they do have the same radii just adds to the beauty of this configuration of circles. :)
Log in to reply
Thanks sir, yes the way you tell to post this problem is really nice. I want to change this problem like you say but I'm unable to change the answer please help......
Log in to reply
Well, the question could go something like this:
In a circle of diameter 1 2 , draw two tangent arcs of radius 6 , and then 1 0 inscribed circles as shown; two of diameter 6 , four red ones each of radius a and four dark blue ones each of radius b . Find a b .
This way the answer is still 1 , but people will have to determine a and b separately. Does that sound o.k.?
Log in to reply
@Brian Charlesworth – thanks sir!!
@Brian Charlesworth – Absolutely correct, Brian. Many thanks for the explanation.
From the picture, we have
( 3 + a ) 2 + 3 2 + a = 6
Solving this, we see that a = 1 , and 1 b is equal to 1 for all real numbers b .