Pellbles
You find some pebbles and arrange them in groups of increasing diamond-shapes as follows:
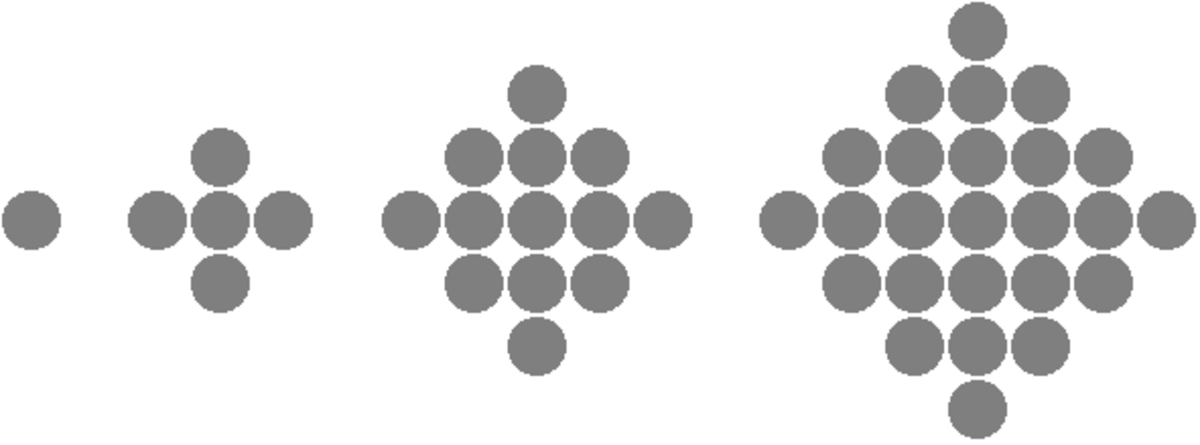
You notice that the first and fourth groupings use a square number of pebbles ( 1 2 = 1 and 5 2 = 2 5 ).
If the pattern continues, how many other groupings would also use a square number of pebbles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice solution! Next challenge: can you come up with a recursive equation for it?
Log in to reply
Let all the solutions of ( n , m ) be denoted as ( n 1 , m 1 ) , ( n 2 , m 2 ) , ( n 3 , m 3 ) , … , where n 1 < n 2 < ⋯ and m 1 < m 2 < ⋯ .
Then for k ⩾ 2 , we have the recursive relations
n k = 6 n k − 1 − n k − 2 − 2 , n 1 = 1 , n 2 = 4 m k = 6 m k − 1 − m k − 2 , m 1 = 1 , m 2 = 5
Voila: ( n , m ) = ( 1 , 1 ) , ( 4 , 5 ) , ( 2 1 , 2 9 ) , ( 1 2 0 , 1 6 9 ) , ( 6 9 7 , 9 8 5 ) , ( 4 0 6 0 , 5 7 4 1 ) , …
Log in to reply
I combined some things to get n k + 1 = 3 n k + 2 2 n k 2 − 2 n k + 1 − 1 , which is the same sequence that you showed. By the way, this sequence is ( OEIS A046090 .
Log in to reply
@David Vreken – Now change the last two paragraph of the question to:
You notice that only the first grouping uses a cube number of pebbles ( 1 3 = 1 ).
Can we find any other such grouping?
The options:
[ ] Yes, finitely many
[ ] Yes, infinitely many
[x] No
I don't know how to prove this but I'm pretty confident of the answer.
Log in to reply
@Pi Han Goh – I'm not sure how to prove it, either, but I did verify that your conjecture is true with a Python program for the first 10,000,000 groupings.
Log in to reply
@David Vreken – Nearly a week late to the party, but here goes: The equation we want to solve in integers is m 3 = 2 n 2 − 2 n + 1
Multiply by 8 : 8 m 3 = 1 6 n 2 − 1 6 n + 8 = ( 4 n − 2 ) 2 + 4
Put x = 2 m and y = 4 n − 2 to get y 2 = x 3 − 4
which is an example of Mordell's equation . Better still, this precise example is solved on page 6 of this awesome paper by Keith Conrad. He shows the only solutions in integers to the above equation are ( x , y ) = ( 2 , ± 2 ) and ( x , y ) = ( 5 , ± 1 1 ) .
The first of these leads to solutions in the original equation ( m , n ) = ( 1 , 0 ) and ( m , n ) = ( 1 , 1 ) . The second gives non-integer values for ( m , n ) so is discounted.
...and yes, I've spent way more of that week than I'd like to admit thinking about this question!
Log in to reply
@Chris Lewis – Wow, nicely done!
@Chris Lewis – You can't just submit your answer here. You have to submit a new problem and post your findings there!
Log in to reply
@Pi Han Goh – Haha, OK, it's posted now (though I really feel it was your question!).
This is obviously opening a can of worms, but what kind of intersections with other sequences of figurate numbers are possible?
Triangular numbers seem fairly easy (there's an obvious pattern if you solve 2 1 m ( m + 1 ) = 2 n 2 − 2 n + 1 for m )
We've done squares, and cubes...how about square pyramidal numbers?
So, trying to solve 6 1 m ( m + 1 ) ( 2 m + 1 ) = 2 n 2 − 2 n + 1
A simple search shows there are some solutions...but how many?
Yup, but only through working some numbers out; the sequence defined by a 1 = 1 , a 2 = 4 and a i + 2 = 6 a i + 1 − a i − 2
makes D ( a i ) a square number for all i .
Log in to reply
@Pi Han Goh - you just beat me to it! It's not too bad to prove that these always give solutions (induction works). Is there an easy way to show there are no other possible solutions?
Log in to reply
@Chris Lewis – What do you mean by no other possible solutions? Your solution clearly demonstrates that there are infinitely many solutions.
Log in to reply
@Pi Han Goh – No other solutions than the ones generated by the recursive formulas. Like, how do we know there isn't a solution between ( 6 9 7 , 9 8 5 ) and ( 4 0 6 0 , 5 7 4 1 ) ? (Without just checking, obviously)
Log in to reply
@Chris Lewis – It's a Pell's equation. You can construct a general formula, (like Binet's formula), then convert it to a recursive formula.
An alternative approach is to note that n − 1 , n , m form a Pythagorean triple; this also leads to Pell's equation.
lol I messed up I had the exact same equation except with (n+1) where m should have been. Agh.
Clever title! I get it now, Pell-bles haha
The n th diamond shape has D ( n ) = n 2 + ( n − 1 ) 2 dots, as illustrated below:
So the equation we want to solve is n 2 + ( n − 1 ) 2 = m 2 where m , n are natural numbers. Rearranging this, 2 n 2 − 2 n + 1 4 n 2 − 4 n + 2 ( 2 n − 1 ) 2 − 2 m 2 = m 2 = 2 m 2 = − 1
which is an example of Pell's equation (hence the problem's title). Since this equation has infinitely many solutions in integers, there are infinitely many diamonds made up of a square number of dots.
The next one is D ( 2 1 ) = 8 4 1 = 2 9 2 .