Pentagon in a Pentagon
The diagonals of a regular pentagon can be used to form a smaller regular pentagon.
The ratio of the areas of the large pentagon to the small pentagon is ϕ n , where ϕ is the golden ratio 2 1 + 5 , and n is an integer.
What is n ?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Nice concise solution!
Very smart solution, I did it with complex trigonometry 😬😬
Please could you explain a little bit more how you get the relationship 1 a − 1 = a − 1 a ?
Log in to reply
Okay, I've added a figure and some more comments in my solution.
Log in to reply
Thank you! Your fugure helps a lot and I totally understand your proof which is really great!! I did way more complicated (but I got it)... Last, as Peter Macgregor said, I think you swapped the " 1 " and the " a " but it is only a detail!
Thank you for sharing so good solutions!
I'm convinced you have a great solution, but I can't follow it.
Should '1' and 'a' be swapped in the first sentence (or perhaps in the diagram)? Also, could you state which two similar triangles you are using?
Thanks
Log in to reply
...oh, right. Let me fix that.
(Fixed) Thanks for the catch.
Hi, This solution is Brilliant (no pun inteded). However I'm not sure how do you get phi^4 from phi^2?
Log in to reply
The problem asks for the ratio of the areas, so that has to be squared. That's how we end up with ϕ 4 , once we've determined a to be ϕ 2 .
Log in to reply
I see, thank you for your answer! I didn't know one could just square a ratio to get from dimension 1 (segments) to dimension 2 (areas). Is it possible to use the same trick to get the ratio of 2 volumes just by getting the ratio of 2 segments used to form the given 2 volumes (to the third power)? (For a regular Dodecahedron for example)
Log in to reply
@Gueddach Noureddine – Well, with volumes, you need to cube the ratio. For example, a box of side 2 has 2^3 = 8 the volume of a box of side 1. The rato of sides is 2, while the ratio of volumes is 8.
Log in to reply
@Michael Mendrin – Thank you very much, sir.
As we all forgot polygon's properties ... this solution becomes brilliant indeed!
我觉得这个想法很棒,非常简单,我直接认为比例为黄金分割
Only to get the correct answer, it might be easier to estimate..
Since n is an integer, make a list of ϕ 's powers:
ϕ ≈ 1 . 6 1 8 ϕ 2 ≈ 2 . 6 1 8 ϕ 3 ≈ 4 . 2 3 6 ϕ 4 ≈ 6 . 8 5 4 ϕ 5 ≈ 1 1 . 0 9 0 ⋮
so the answer may be 3 or 4
I also didn't understand why we would even get 3 chances to guess an integer that is clearly approximately equal to 4. Actually I'm clueless why half the people seem to fail this problem...
The simplest way to find this integer is to simply guess how many of those blue pentagons fit in the whole pentagon. We can fit 5 extra blue pentagons (on top of the one already drawn) in the corners of the big pentagon, and will even have a small amount of space left (5 small triangles), so ϕ 4 ≈ 6 . 8 5 seems about right intuitively.
Log in to reply
Sometimes when I come to a problem like this where I could guess, I think it won't really be rewarding, and just hit view solutions. Hence I get it wrong. I think that I may not be the only one. Plus people may not think of this trick and just hit view solutions anyways, or guess 1 2 3 :P
Log in to reply
Hah, many students at school may use this method, since what they only need in the exams are the correct answers.. That's really an efficient way to solve problems sometimes.. Get the correct answer, and we can stop for a while to think carefully about the principles behind these (easy) problems..
This is exactly how I did it. However I was doing it in me head and rounded each time to the nearest 0.5 so I got:
ϕ ≈ 1 . 5 ϕ 2 ≈ 2 ϕ 3 ≈ 3 ϕ 4 ≈ 4 . 5 ϕ 5 ≈ 7
So it took more than one guess.
That’s exactly what I did.
Just eying the area to be at least five lots of the blue area plus more, so for seemed way too little, and eleven double my “thumb nail” estimate. So 6.854 it had to be
To begin with, it is known that the area of a reguliar polygon is proportional to the square of th lenght of its side. Be A the area of the bigger pentagon and A ′ of the smaller one, and respectively a and a ′ the lenght of their sides.
A = α . a 2 and A ′ = α . a 2 **
Meaning : ϕ n = A ′ A = ( a ′ a ) 2
From here, we can use Thales' theorem to write :
a ′ a = b B (see the figure for B and b)
Now, let's find B and b expressions.
Using Pythagore's theorem in red and green triangles, and knowing that a pentagon's internal angle is 108° (purple filled arc on figure), we get :
b = 2 . c o s ( 3 6 ) a (108/3 = 36, orange arc on figure)
B = 2 . a . s i n ( 5 4 ) (108/2 = 54, blue arc on figure)
Hence : ϕ n = ( 4 . s i n ( 5 4 ) . s i n ( 3 6 ) ) 2
n . l o g ( ϕ ) = l o g ( ( 4 . s i n ( 5 4 ) . s i n ( 3 6 ) ) 2 )
| n = l o g ( ϕ ) l o g ( ( 4 . s i n ( 5 4 ) . s i n ( 3 6 ) ) 2 ) |
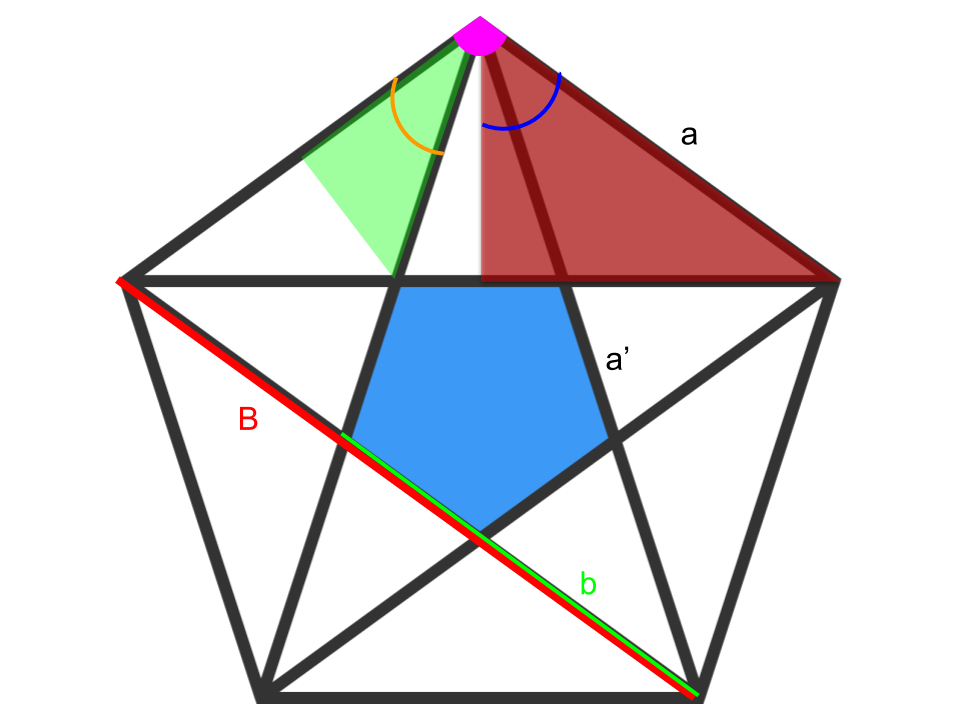
**out of curiosity, I've checked on wikipedia the value of the ratio : α ≈ 1 , 7 2
Wow, I thought everyone would have used the same simple, intelligent methods. Glad to see that I'm not the only one making things complicated.
We know the interior angle of pentagon is 1 0 8 ∘
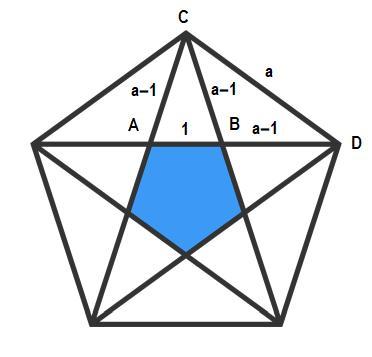 Thus,
∠
C
B
A
=
7
2
∘
and
∠
B
C
D
=
3
6
∘
Thus,
∠
C
B
A
=
7
2
∘
and
∠
B
C
D
=
3
6
∘
So, the side ratio A B C D = A B / 2 C D / 2 = c o s 7 2 c o s 3 6 = 2 1 (3+ 5 ) = ϕ 2 ; you may check the rational form of cos 3 6 ∘ and cos 7 2 ∘ to get the value
And area ratio is ϕ 4
The small pentagon is also regular. Its side length is
x=a/4(cos 36°)^2 (using sine law)
(a= side length of large pentagon)
The area of the large pentagon is
na^2/4(cot π/n)
The area of the small penta gon is
nx^2/4(cot π/n)
Therefore the ratio is (a/x)^2
=[4(cos36°)^2]^2
=[4×{(√5+1)/4}^2]^2
=[(√5+1)/2]^4
Answer=<<<<<4>>>>>😃
In reference to Michael Mendrin's drawing, we have that angle at C is 108deg (=540/5) and angle at BDC is 36deg (because the triangle with top at C and horizontal opposite side is isocele). This means that ACB is 36deg (=108-2 36). From that we can infer - Length of segment from C to mid[A,B] = sin(BDC)=sin36 with unit side of large pentagon - Length of segment CB = (sin36)/cos(ACB/2)=cos18 - Length of blue pentagon side (segment AB) = 2 (sin36/cos18) sin(ACB/2) = 2 (sin36/cos18) sin18 = 4 (sin18)^2 = 0.3820 (by sin(2*18) formula) By testing, 0.3820 = 1/phi^2. Thus, ratio of large/small pentagon side is phi^2. The ratio of area is the square of it, i.e. phi^4.
A solution based on guesswork: Call the side of the small pentagon 1. This is the base of a small isosceles triangle. I'm guessing the other two sides are length ϕ . One of these sides is the base of a bigger isosceles triangle whose other sides are therefore (another guess) ϕ squared. One of these 'other sides' is the length of the big pentagon. So if the proportion of the lengths is ϕ squared, the proportion of the area is ϕ to the power of 4.
Let the side of the blue pentagon be 1 and that of the large pentagon be a . Then we have, through similiar isoceles triangles
1 a − 1 = a − 1 a
which yields a = 2 1 ( 3 + 5 ) = ϕ 2 . Thus the ratio of the areas is 1 : ϕ 4
Triangles Δ A B C and Δ B C D are isosceles. This means A C = B C = B D = a − 1 . Furthermore, because angles ∠ A C B = ∠ A D C *, isoceles triangles Δ A B C and Δ A D C are similiar, so that the equation to solve for a then follows.
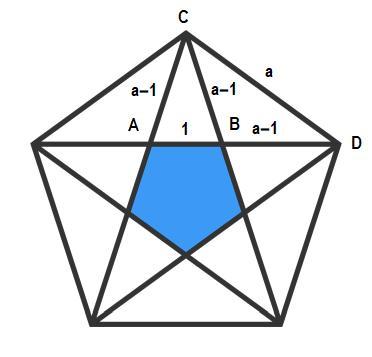 *Note: In a regular polygon, the angle between any two consecutive diagonals are the same. Hence,
∠
A
C
B
=
∠
B
C
D
=
∠
C
D
B
so that
∠
A
B
C
=
∠
B
A
C
=
∠
A
C
B
+
∠
B
C
D
, thus establishing that triangle
Δ
A
C
D
is isosceles.
*Note: In a regular polygon, the angle between any two consecutive diagonals are the same. Hence,
∠
A
C
B
=
∠
B
C
D
=
∠
C
D
B
so that
∠
A
B
C
=
∠
B
A
C
=
∠
A
C
B
+
∠
B
C
D
, thus establishing that triangle
Δ
A
C
D
is isosceles.