Pentagons and Ratios
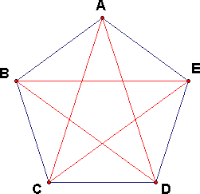 Each diagonal of the convex pentagon
A
B
C
D
E
cuts off of it a triangle of unit area. Calculate the area of the pentagon
A
B
C
D
E
, and express the answer to the three decimal places.
Each diagonal of the convex pentagon
A
B
C
D
E
cuts off of it a triangle of unit area. Calculate the area of the pentagon
A
B
C
D
E
, and express the answer to the three decimal places.
Note: The pentagon need not be regular.
The answer is 3.61803.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution. I did this slightly differently by breaking up the pentagon into 3 isosceles triangles. Let the intersection of lines C E and A D be Q . Then triangles △ A Q C , △ A E D , △ A B C are all congruent with an area of 1. Then we only need to find the area of triangle △ C Q D
Let the point of intersection of B D and C E be T . Then the ratio of the area of triangles △ D Q T , △ E Q D , △ C T D to the area of triangle △ C E D must sum to 1. Also note that the ratio of the areas will be equivalent to the area of that triangle
With our extensive and useless knowledge (acquired from this problem ) we know that the ratio of △ C E D △ C T D = ϕ 2 1 .
Let the ratio of △ C D E △ D Q T = x Thus (note that ϕ = 2 1 + 5 )
ϕ 2 1 + ϕ 2 1 + x = 1
2 + ϕ 2 x = ϕ 2
ϕ 2 x = ϕ 2 − 2
ϕ 2 x = ϕ 1
x = ϕ 3 1
Thus summing the areas we have
ϕ 2 1 + ϕ 3 1 = ϕ 1
So our answer is 3 + ϕ 1
Log in to reply
Very nice. :) I like how you featured ϕ , (you had me busy these verifying all those beautiful results and revisiting the question you had posted). One small typo to mention; I think that you meant to write that T was the point of intersection of C E and B D .
Note that you made the assumption that we're dealing with a regular pentagon. This is not necessary. See this problem .
Log in to reply
I think the given data implies that it is regular. It says each diagonal and does not give any a d d i t i o n a l data.. And, I think, without assuming regular, we can not solve the problem. The problem you have mentioned has given additional data.
Log in to reply
Saying that a polygon has a diagonal doesn't make it a regular polygon.
In my problem, I provided additional information so as to force solutions to not talk about the regular pentagon case. All that we actually need, is [ A B C ] = [ B C D ] = [ C D E ] = [ D E A ] = [ E A B ] . The use of angles is redundant (and that is part of the point of the question).
Log in to reply
@Calvin Lin – Does this mean that my solution doesn't hold as well.
And I can't seem to imagine a pentagon without 5 equal triangles that aren't 108, 36,36.
@Calvin Lin – Thanks for the explaining. I meant that, since each diagonal c u t s e q u a l a r e a . How ever your comment is correct. My thinking was wrong. So some of our proofs are not correct.
May not be the nicest solution, but short enough: First we compute ∣ △ A B C ∣ ∣ △ A C D ∣ = sin 3 6 ∘ sin 7 2 ∘ = C D A D = A E B E . Now let B E intersect A D intersect at F . Note that the ratio we had before can also be expressed as B A B F + A E F E . Angle chasing around, we have B A = B F since △ A B F is isosceles, and A E F E = B E A E by similar triangles △ B A E and △ A F E . So if we let the required ratio be x , we have established A E B E = B A B F + A E F E ⟺ x = 1 + x 1 which at this point can be solved as a quadratic equation (multiply both sides by x ) or recognised as the well-known ratio ϕ = 1 . 6 1 8 … . Hence ∣ △ A C D ∣ = ϕ , and the answer is ∣ A B C D E ∣ = ∣ △ A B C ∣ + ∣ △ A C D ∣ + ∣ △ A D E ∣ = 2 + ϕ ≈ 3 . 6 1 8 .
Honestly this is similar to Brian's and Trevor's solutions, just avoiding most of the trigonometry/assumed knowledge. In this solution I think I would derive on the way some of the identities Trevor mentioned, and that cos 3 6 ∘ = 2 ϕ .
Also I should mentioned at the start I used the area formula 2 1 a b sin θ and the Sine Law, and skipped a lot of "trivial" angle chases throughout (left as an exercise to the reader :D).
Note that you made the assumption that we're dealing with a regular pentagon. This is not necessary. See this problem .
∠ b e t w e e n p e t a g o n s i d e s = 5 5 ∗ 1 8 0 − 2 ∗ 1 8 0 = 1 0 8 o , ∠ A B C = ∠ B A E = 1 0 8 o , A B = B C ∴ ∠ B A C = 3 6 o = ∠ E A D b y s y m m e t r y ∴ ∠ C A D = 3 6 o . L e t x = A C . ∴ f o r i s o s c e l e s Δ A B C 1 = A r e a = ( 2 x ) 2 ∗ S i n 3 6 o ∗ C o s 3 6 o . B u t A r e a i s o s c e l e s Δ C A D = ( 2 x ) 2 ∗ S i n 1 8 o ∗ C o s 1 8 o = ( 2 x ) 2 ∗ 2 1 S i n 3 6 o . A r e a Δ C A D = 1 ∗ C o s 3 6 o 2 = 1 . 6 1 8 . P e n t a g o n A r e a = A r e a s Δ s { A B C + C A D + D A E } = 1 + 1 . 6 1 8 + 1 = 3 . 6 1 8 . After seeing the other nice and detailed solutions, I would rather avoid giving mine. I am giving just to show how to shorten the calculations.
Note that you made the assumption that we're dealing with a regular pentagon. This is not necessary. See this problem .
We know that the areas of Δ A B C and Δ A D E are 1 . Hence we are required to compute only the area of Δ A C D .
Visualizing the circumcircle of the pentagon we find that ∠ C A D = ∠ C E D since they are angles in the same segment of the circumcircle..
We also have ∠ C E D = ∠ D C E since Δ C D E is isosceles.
Applying the angle sum property in Δ C E D we have 2 ∠ C E D + ∠ C D E = π
or 2 ∠ C E D + 5 3 π = π ⟹ ∠ C E D = 5 π
Here we have used the fact the the interior angle of a regular n-gon is n ( n − 2 ) π where n = 5 in this case.
So we now have ∠ C E D = ∠ C A D = 5 π
Let d be the length of any diagonal then area of Δ A C D = 2 1 d 2 sin ( ∠ C A D ) = 2 1 d 2 sin ( 5 π )
Let a be the side length, then from the law of cosines, d 2 = a 2 + a 2 − 2 a 2 cos ( 5 3 π ) = 2 a 2 ( 1 − cos ( 5 3 π ) ) = 2 a 2 ( 1 + cos ( 5 2 π ) ) = 4 a 2 cos 2 ( 5 π )
Also since we the diagonals cut off unit triangles, we know 2 1 a 2 sin ( 5 3 π ) = 1
or, 2 1 a 2 sin ( 5 2 π ) = a 2 sin ( 5 π ) cos ( 5 π ) = 1
Using all of this in ∣ Δ A C D ∣ = 2 1 d 2 sin ( 5 π ) , we get
∣ Δ A C D ∣ = 2 cos ( 5 π ) = 2 cos ( 3 6 ∘ ) = 2 2 ϕ = ϕ
Where ϕ is the Golden Ratio and ϕ ≈ 1 . 6 1 8 …
So we finally have area of the pentagon = 2 + ϕ ≈ 3 . 6 1 8 …
Note that you made the assumption that we're dealing with a regular pentagon. This is not necessary. See this problem .
Let the side lengths of the pentagon be a . Then since the interior angles of a regular pentagon are 1 0 8 ∘ we have that, for example, the area of Δ B C D is
2 1 a ∗ a sin ( 7 2 ∘ ) = 1 ⟹ a 2 = sin ( 7 2 ∘ ) 2 .
Now a regular pentagon can be divided into 5 congruent isosceles triangles each with a base of length a and two base angles of 5 4 ∘ each. Thus the area of the pentagon is
5 ∗ 2 1 a ∗ 2 a tan ( 5 4 ∘ ) = 4 5 a 2 tan ( 5 4 ∘ ) .
Substituting in the value for a 2 found above, we see that the area of the pentagon is
4 5 ∗ sin ( 7 2 ∘ ) 2 ∗ tan ( 5 4 ∘ ) = 2 5 2 sin ( 3 6 ∘ ) cos ( 3 6 ∘ ) cot ( 3 6 ∘ ) = 4 5 csc 2 ( 3 6 ∘ ) .
Now sin ( 3 6 ∘ ) = cos ( 5 4 ∘ ) ⟹ sin ( 2 ∗ 1 8 ∘ ) = cos ( 3 ∗ 1 8 ∘ ) .
Now using the identities
sin ( 2 x ) = 2 sin ( x ) cos ( x ) and cos ( 3 x ) = 4 cos 3 ( x ) − 3 cos ( x ) , we see that
sin ( 2 x ) = cos ( 3 x ) ⟹ 2 sin ( x ) cos ( x ) = 4 cos 3 ( x ) − 3 cos ( x )
⟹ cos ( x ) ( 2 sin ( x ) − 4 cos 2 ( x ) + 3 ) = 0 .
Now since cos ( x ) = 0 when x = 1 8 ∘ we must have that
2 sin ( x ) − 4 cos 2 ( x ) + 3 = 0 ⟹ 4 sin 2 ( x ) + 2 sin ( x ) − 1 = 0
⟹ sin ( x ) = 8 − 2 + 4 + 1 6 = 4 − 1 + 5 ,
where we took the positive root since we know that sin ( 1 8 ∘ ) > 0 .
Now cos ( 1 8 ∘ ) = 1 − sin 2 ( 1 8 ∘ ) = 4 1 1 0 + 2 5 , so
sin ( 3 6 ∘ ) = 2 sin ( 3 6 ∘ ) cos ( 3 6 ∘ ) = 8 1 ( − 1 + 5 ) 1 0 + 2 5 .
and so sin 2 ( 3 6 ∘ ) = 8 1 ( 5 − 5 ) .
Thus the area of the given pentagon is
5 − 5 1 0 = 2 5 + 5 = 3 . 6 1 8 to 3 decimal places.