Pentagons in Pentagons 2
The midpoints of adjacent sides of a regular pentagon are joined to make a smaller second pentagon, the midpoints of adjacent sides of the second pentagon are joined to make an even smaller third pentagon, and the diagonals of the third pentagon are joined to make the smallest fourth pentagon.
Find the ratio of the area of the largest pentagon to the area of the smallest pentagon.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I didn't think of this approach, but I love it! It's simple and clean.
Log in to reply
I tried all kinds of way to "neatly tesselate the large pentagon", but couldn't come up with anything nice. It seemed very tantalizing that the space between the large and small pentagon is 15 times the smaller one, or 3 of the small pentagon repeated 5 times around. No luck yet.
Log in to reply
Your comments inspired me to break the whole diagram up into 2 different types of congruent triangles:
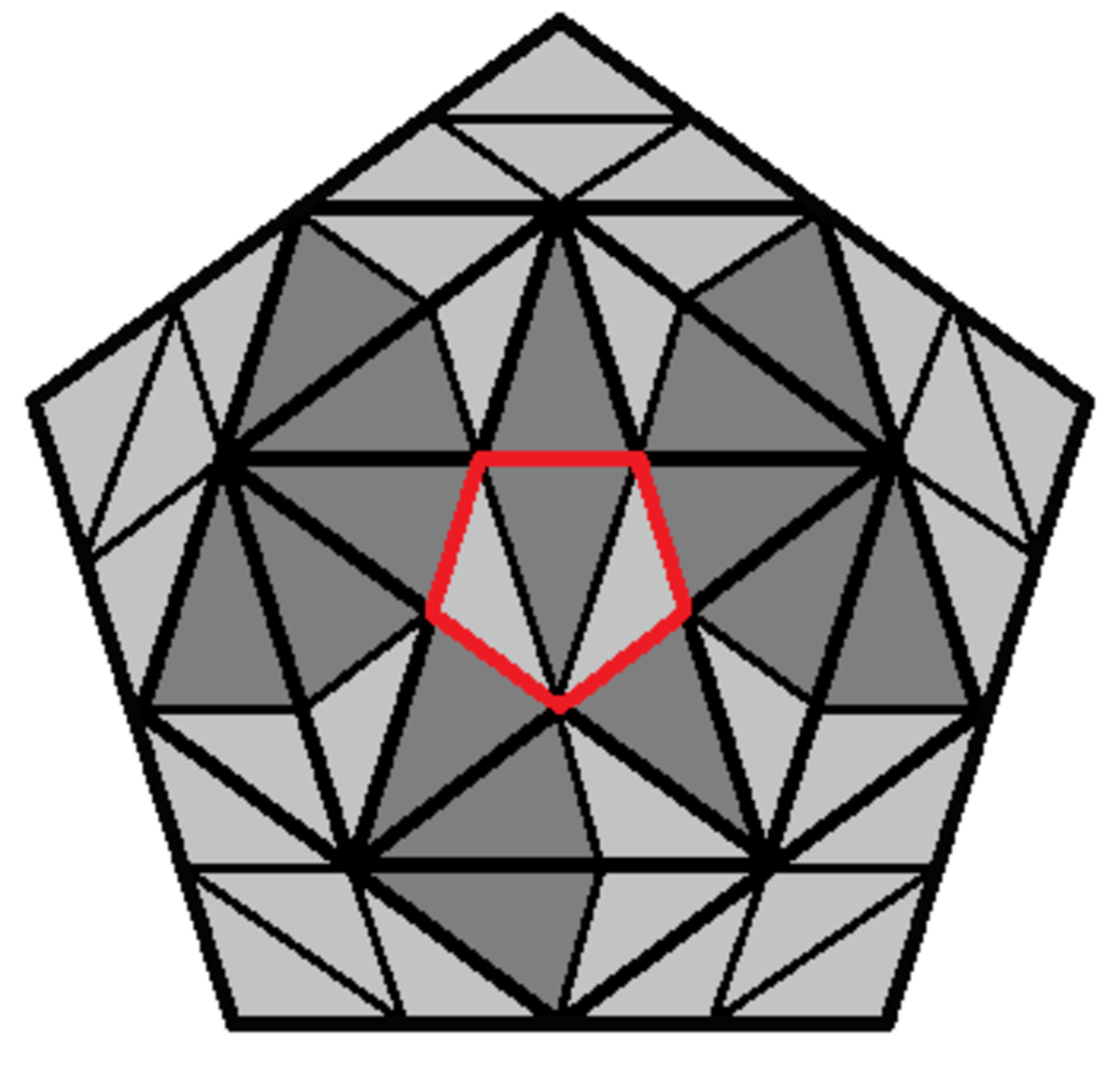
The small pentagon in the center has 2 light gray triangles and 1 dark gray triangle, and the whole pentagon has 3 2 light gray triangles and 1 6 dark gray triangles, which is 1 6 times as many.
Log in to reply
@David Vreken – Yes, this is one of the configurations I've considered, except that I made the area outside of the small pentagon rotationally symmetric. In any case, it sufficiently proves the answer. How are you able to use MS Paint to draw something like this? I've looked at MS Paint.
Log in to reply
@Michael Mendrin – By the way, this is the genesis of Penrose Tiling . I wonder if he went through the same thing in coming up with his tiles?
Log in to reply
@Michael Mendrin – Thanks for sharing the article! I love stuff like this.
@Michael Mendrin – To draw this in MS Paint, I used the pentagon drawing tool (but had to guess at what size made it regular) and then the line tool (approximating where to start and end segments) and then lastly the fill function to color it in. With all the approximations and guesswork MS Paint is probably not the best choice for drawing math diagrams but it is what I am most comfortable with and it gets the job done.
Consider the relationship between a regular pentagon and the regular pentagon formed by the star inside it (the yellow, orange, and red below), and consider the relationship between a regular pentagon and the regular pentagon formed by joining its midsegments (the green and blue below), all labelled by the letters in the picture given. Let the sides of the red pentagon be x , the sides of the yellow pentagon be y , the sides of the green pentagon be v , and the sides of the blue pentagon be w .
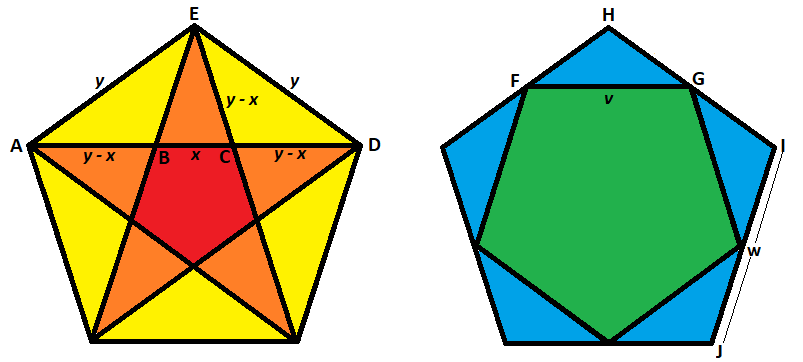
Then C D = B D − B C , and since B D = D E = y and B C = x , C D = y − x . By symmetry, C D = C E = B E = A B = y − x . So A D = A B + B C + C D = ( y − x ) + x + ( y − x ) = 2 y − x .
Since △ A E D is similar to △ D C E , A D D E = D E C D , or 2 y − x y = y y − x , and this solves to y = 2 3 + 5 x , or y = ϕ 2 x , where ϕ = 2 1 + 5 , the golden ratio. So the sides of a regular pentagon are greater than the sides of the regular pentagon formed by the star inside it by a factor of ϕ 2 .
Additionally, since △ F H G is also similar to △ D C E , F G D E = H G C D , or v y = 2 1 w y − x , and since y = ϕ 2 x and ϕ 2 − 1 = ϕ , this solves to w = ϕ 2 v . So the sides of a regular pentagon are greater than the sides of the regular pentagon formed by joining its midsegments by a factor of ϕ 2 .
In the problem, the smallest pentagon is formed by a star in a pentagon formed by the joining the midsegments of a pentagon formed by joining the midsegments of the largest pentagon, so the sides increased by a factor of ϕ 2 ⋅ ϕ 2 ⋅ ϕ 2 = 4 . Therefore, the areas increased by a factor of 4 2 = 1 6 .
Follow the side length 1 of the small pentagon in the center. Using isosceles triangles and a parallelgram, it can be readily seen that the side length of the large pentagon is 4 .