Pentallipse

Computer Science Level 5

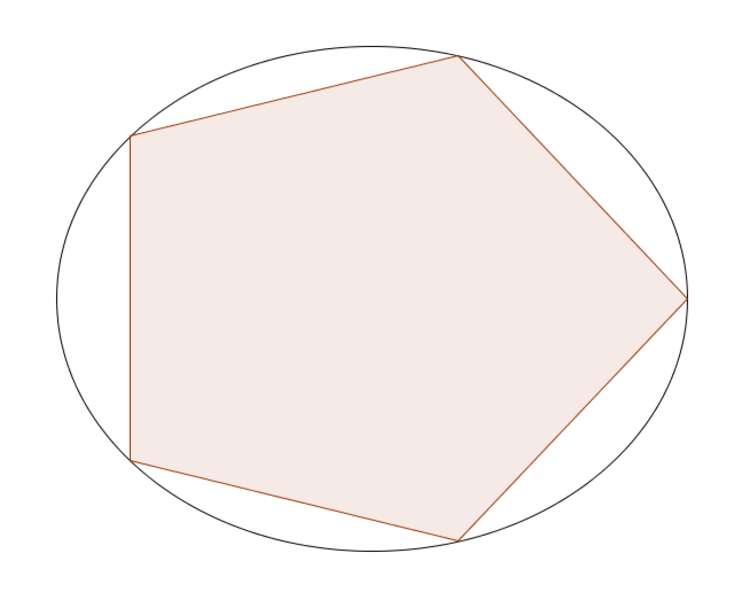Construct an ellipse with major axis 3 and minor axis 4. Now arrange 5 points on the ellipse such that the arc length between each pair of consecutive points is equal. What is the area of the pentagon formed by these points? (Image not to scale).

The answer is 28.403.

2 solutions

Chandler West
May 26, 2014

The parametric equation of an ellipse is

$x(t) = a*cos(t)$

$y(t) = b*sin(t)$

The arc length formula between $t_1$ and $t_2$ on the ellipse is therefore:

$f(t_1, t_2)$ = $\int_{t_1}^{t_2} \sqrt{(-a sin(t))^2 + (b cos(t))^2} dt$

This is an elliptic integral, so we will use a numerical integrator as well as a binary search to find the angles:

import math
import mpmath

def binary_search(f, t1, goal, a, b):

    m = (a+b)/2.0
    t = f(t1, m)
    if abs(t - goal) < 10**-12: # stop when precision is reached
        return m
    if t < goal:
        return binary_search(f, t1, goal, m, b)
    else:
        return binary_search(f, t1, goal, a, m)

a = 3 # major axis
b = 4 # minor axis

f = lambda t: math.sqrt((-a*math.sin(t))**2 + (b*math.cos(t))**2) # arc length formula
g = lambda t1, t2: mpmath.quad(f, [t1, t2]) # finds the arc length between t1 and t2

P = 5 # number of points we want to find
C = g(0.0, 2*math.pi) # total circumference of the ellipse, integrating from 0 to 2*pi
goal = C / P # each segment should be this long

L = [0.0] # initialize our list
for i in range(P-1): # find the next angle from the previous
    L.append(binary_search(g, L[-1], goal, 0.0, 2*math.pi))

print [[a*math.cos(t), b*math.sin(t)] for t in L] # coordinates of points

Now use whatever method you like to find the area of the points.

Actually a=3 and b=4 are the semi-major and semi-minor axes of the ellipse, not the major and minor axes.

Mark Hennings - 7 years ago

This seems to suggest that the area is independent of the initial point chosen. Is there a mathematical explanation for that?

Note that you can edit the solution, by clicking on the pencil to the top right.

Calvin Lin Staff - 7 years ago

Honestly, I don't know. Empirically it seems to be true (just from testing random points a bunch of times), but I'm having trouble justifying that since I don't know how to formulate the problem without using inverse elliptic integrals.

Chandler West - 7 years ago

The more I think about it the less convinced I am the area is independent. I believe the difference is very small however, which led to the confusion since my solution to the problem isn't exact.

Chandler West - 7 years ago

@Chandler West – I'm inclined to agree with you, that the difference in area was small and hence not noticed. This ellipse to too 'close' to a circle, which is why we seem to get the result.

Calvin Lin Staff - 7 years ago

Awesome problem!

Thaddeus Abiy - 7 years ago

Sweet! I just have a 2 questions.

1.) How accurate/precise is your numeric approximation? If you can, could you provide an extremely approximate answer?

2.) How much does the area deviate as the starting point is changed (if any deviation at all occurs)

Milly Choochoo - 7 years ago

Aayush Mani
Jun 6, 2014

The parametric equation of an ellipse is The arc length formula between and on the ellipse is therefore: = This is an elliptic integral, so we will use a numerical integrator as well as a binary search to find the angles: import math import mpmath

def binary_search(f, t1, goal, a, b):

m = (a+b)/2.0
t = f(t1, m)
if abs(t - goal) < 10**-12: # stop when precision is reached
    return m
if t < goal:
    return binary_search(f, t1, goal, m, b)
else:
    return binary_search(f, t1, goal, a, m)

a = 3 # major axis b = 4 # minor axis

f = lambda t: math.sqrt((-a math.sin(t)) 2 + (b math.cos(t)) 2) # arc length formula g = lambda t1, t2: mpmath.quad(f, [t1, t2]) # finds the arc length between t1 and t2

P = 5 # number of points we want to find C = g(0.0, 2 math.pi) # total circumference of the ellipse, integrating from 0 to 2 pi goal = C / P # each segment should be this long

L = [0.0] # initialize our list for i in range(P-1): # find the next angle from the previous L.append(binary_search(g, L[-1], goal, 0.0, 2*math.pi))

print [[a math.cos(t), b math.sin(t)] for t in L] # coordinates of points Now use whatever method you like to find the area of the points.

@Calvin Lin

Thaddeus Abiy - 7 years ago

Pentallipse

The answer is 28.403.

2 solutions

0 pending reports