Perfect In-Shuffles

Probability Level 2

A magician is so good at shuffling that his shuffles are always perfect in-shuffles. That means his shuffles are done in the following two steps:

Split the pile of cards exactly in half.
Interleave the top half with the bottom half such that every second card is from the top half.

If he started with six cards and shuffled thrice, he would get the original arrangement back.

If he started with a deck of 52 cards, how many shuffles would he need to get the original arrangement back?

The answer is 52.

10 solutions

Mark Hennings
Feb 10, 2018

If the cards positions are numbered $1$ to $52$ (with $1$ being the top card), then the perfect Faro in-shuffle (as it is called) provides the following permutation of the cards: $j \; \mapsto \; 2j \hspace{1cm},\hspace{1cm} 26+j \; \mapsto 2j-1 \hspace{3cm} (1 \le j \le 26)$ In cycle notation we discover that this is a $52$ -cycle: $\begin{array}{cccccccccccccccccccccccccc} (1 & 2 & 4 & 8 & 16 & 32 &11 & 22 & 44 & 35 & 17 & 34 & 15 & 30 & 7 & 14 & 28 & 3 & 6 & 12 & 24 & 48 & 43 & 33 & 13 & 26 \\ 52 & 51 & 49 & 45 & 37 & 21 & 42 & 31 & 9 & 18 & 36 & 19 & 38 & 23 & 46 & 39 & 25 & 50 & 47 & 41 & 29 & 5 & 10 & 20 & 40 & 27 ) \end{array}$ which therefore has order $\boxed{52}$ .

If the riffle shuffle is done the other way, so that the top card always remains on top and the bottom card always remains on the bottom (this is the Faro out-shuffle), the order of the corresponding permutation is only $8$ (a fact well-known to stage magicians).

More succinctly, the mapping is $j \mapsto 2j \pmod{53}$ . It then remains to show that the smallest solution to $2^n \equiv 1 \pmod{53}$ is $n= 52$ , or equivalently that 2 is a primitive root mod 53.

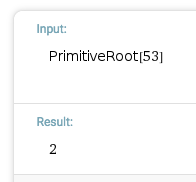
Calvin Lin Staff - 3 years, 3 months ago

One could save some time by only calculating the cycle to element 26 since its length must be a divisor of 52.

Keine Angabe - 3 years, 3 months ago

It is not true that all elements of the group $S_n$ of permutations of $n$ symbols have order dividing $n$ (you seem to be claiming that this is true for $S_{52}$ ). For example, $S_5$ contains $(12)(345)$ , which has order $6$ .

Mark Hennings - 3 years, 3 months ago

To add on, the assumption that Keine was making is "the cycles of the elements have the same length". For example, it might have been possible that cards 1 and 52 just swap positions, while the other cards cycle through.

And that is why my interpretation of the group action as "multiplication by 2 in $\mathbb{Z}_{n+1}$ " gives us so much more information. E.g. In the illustrated case of $n=6$ , note that $2^3 \equiv 1 \pmod{7}$ (hence 2 isn't a primitive root so the answer isn't 6).

(Edit: This line is false.) We know what the group action is, and can properly conclude that "the cycles have the same length" and that the "answer is the order of 2 mod n, hence is a divisor of n".

Calvin Lin Staff - 3 years, 3 months ago

@Calvin Lin – Agreed, the structure of $\mathbb{Z}_{53}^\times$ is really useful, particularly since we know that it is a cyclic group of order $52$ . In fact, the fact that the order of the shuffle is the order of $2$ in this cyclic group is what makes Keine's observation true after all! We do need to note, however, that we are working with an element of $C_{52}$ , and not just an element of $S_{52}$ .

Mark Hennings - 3 years, 3 months ago

@Mark Hennings – Oh, actually I lied in my last comment. Let me write it up properly.

Calvin Lin Staff - 3 years, 3 months ago

So what size of cycle of this type, besides 6, will have its order less than its size?

Nicholas Palevsky - 3 years, 3 months ago

Thanks for your solution Mark. There is one small mistake in your list, after the 50 there should follow a 47 (and then the 41). (50-26)*2-1=47

Edit: Thanks Calvin, I have corrected my mistake.

Alexander Zwink - 3 years, 3 months ago

Thanks for checking the details and noticing that typo! It should be $50 \rightarrow 47 \rightarrow 41$ . I have updated the entry accordingly.

Note that your arithmetic is incorrect, as $(50-26) \times 2 - 1 = 47$ .

Calvin Lin Staff - 3 years, 3 months ago

Thanks for spotting the typo...

Mark Hennings - 3 years, 3 months ago

8 was my answer...

Krzysztof Komarnicki - 3 years, 3 months ago

I think it started getting the same number from 10 cards onwards.

Adarsh Adi - 3 years, 3 months ago

Calvin Lin Staff
Feb 20, 2018

This is a generalization where $n = 26$ is used in the problem, and $n = 3$ is used in the illustrated example.

As Mark pointed out, the permutation is:

$j \; \mapsto \; 2j \hspace{1cm},\hspace{1cm} n+j \; \mapsto 2j-1 \hspace{3cm} (1 \le j \le n)$

Notice that we can simplify this to $j \mapsto 2j \pmod{2n+1}$ , where we restrict to the cannonical residue classes (IE from 0 to $2n$ ).

Let's write this out explicitly.
Consider $\mathbb{Z}_{2n+1} ^\times$ , where the $^\times$ indicates that we removed the 0 element (and there is no card corresponding to position 0).
Then, shuffling the cards can be represented as $\phi : \mathbb{Z}_{2n+1} ^\times \rightarrow \mathbb{Z}_{2n+1} ^\times$ , $\phi (x) = 2x$ .
The problem is equivalent to asking for the smallest $k$ such that $\phi^k (x) = x \, \forall x$ . (This is equivalent to saying that $\phi^k$ is the identity function on $\mathbb{Z}_{2n+1}$ .)

Clearly, if $k = ord_{2n+1} (2)$ , then by definition $2^k \equiv 1 \pmod{2n+1}$ and hence $2^k x \equiv x \pmod{2n+1} \forall x$ .
Conversely, by picking $x=1$ , we require that $2^k \equiv 1 \pmod{2n+1}$ . Hence, $k$ must be a multiple of $ord_{2n+1} (2)$ .
Thus, this shows that the smallest $k = ord_ {2n+1} (2)$ .

For $n = 3$ , we can check that $2^1 \equiv 2, 2^2 \equiv 4, 2^3 \equiv 1 \pmod{7}$ , and hence $k = ord_7 2 = 3$ .
For $n = 26$ , it requires a bit of work to check that $2 ^ 4 \not \equiv 1 \pmod{53}$ and $2^{26} \not \equiv 1 \pmod{53}$ , in order for us to conclude that since the order is a divisor of 52, but not a divisor of 4 or 26, hence it can only be 52.

Food for thought:

True or false: The answer must divide $2n$ . (Hint: False. What is the smallest counterexample?)
True or false: Fix $n$ . Each card cycles through the same number of positions. (Hint: False. What is the smallest counterexample?)
How does this change if there is an odd number of cards? The bottom half would have more cards, so that every second card is from the top half.

(Read the comments after you have thought about this.)

In general, $\mathbb{Z}_{2n+1}$ is a ring, but not a field. Consequently, the set $\mathbb{Z}_{2n+1}^\times$ of nonzero numbers modulo $2n+1$ does not form a group (except when $2n+1$ is prime). However the set $\mathcal{U}(\mathbb{Z}_{2n+1})$ of numbers modulo $2n+1$ that are coprime to $2n+1$ (the units of $\mathbb{Z}_{2n+1}$ ) do form a group of order $\phi(2n+1)$ , and $2$ is an element of this group. Thus the order of $2$ divides $\phi(2n+1)$ .

If $n$ is $1,2$ , then $2n+1$ is prime and $2$ is a primitive root, so generates a $2n$ -cycle. If $n=3$ then $2n+1$ is prime, but $2$ is not a primitive root. It generates the $3\times3$ -cycle $(1\;2\;4)(3\;6\;5)$ .

When $n=4$ we see that $\phi(9) = 6 \neq 8$ , so we are likely to have problems. As a unit, $2$ has order $6$ , and it generates the permutation $(1\;2\;4\;8\;7\;5)(3\;6)$ . This makes the answer to both question 1 and question 2 "false, consider $n=4$ ".

If there are an odd number of cards, the bottom card always stays on the bottom, and we are performing a perfect in-shuffle on the other cards on top of it

Mark Hennings - 3 years, 3 months ago

Perfect! After making a false comment, I decided to layout the underlying structure of the shuffle, in which case our understanding of abstract algebra allows us to conclude what is going on.

To provide a more layman explanation of the food for thought:

In actuality, the answer must divide $\phi(2n+1)$ . In the cases where $2n + 1$ is prime (e.g. $n = 3, 26$ ) then $\phi(2n+1) = 2n$ and so the answer must divide $2n$ . In cases when $2n+1$ is composite, then we cannot conclude that the answer must divide $2n$ .
Each card cycles through the same number of positions if and only if the smallest positive integer value of $k_i$ satisfying $2^{ k_i} \times i \equiv i \pmod{2n+1}$ is the same for all $i$ . The latter is clearly true if $2n + 1$ is prime. If $2n+1$ is composite, I do not yet know if this could be true. For example, when $2n+1 = 9$ , we obtain the cycles $(1 \, 2 \, 4 \, 8 \, 7 \, 5 ) (3 \, 6 )$ .
Using the language in the solution, the bottom card corresponds to the residue class of $2n+1$ , and the permutation is $\phi : \mathbb{Z}_{2n+1} \rightarrow \mathbb{Z}_{2n+1}$ , $\phi (x) = 2x$ . We can make similar conclusions about the behvaiour, and in particular, as Mark pointed out, 0 will always be in it's own orbit.

Calvin Lin Staff - 3 years, 3 months ago

For 2, why they are equivalent?

Wong Kwym - 3 years, 1 month ago

@Wong Kwym – Ah, that is a good point. I don't see a proof of that as yet, so I changed it to a single-sided implication.

Calvin Lin Staff - 3 years, 1 month ago

Recognising that for an odd number of cards, if the odd card were in the second pile the last card would always remain last (contrary to Matt 20:16), I put the odd card in the FIRST pile. (I know that the last 2 cards in the first pile will therefore remain adjacent, but only in the first shuffle). This produced some amusing results: for 2n+1 = 13 there were 2 sub-cycles of 4, one of 3 and one of 2, so 12 shuffles are required (LCM of 2,3,4). For 2n+1 = 15 there were sub-cycles of 7 and 8, so to return to starting point we require 56 shuffles. And so on. Whenever 2n cards required 2n shuffles to return to the starting position, then 2n-1 cards required 2n-1 shuffles. This is pretty obvious, come to think about it, as both situations involve doubling mod 2n+1, so the sequences are the same apart from position n in the 2n-1 pack then becoming 2n-1, so that the sequence is n, 2n-1, 2n-3 ..., whereas for the 2n pack it's n, 2n, 2n-1, 2n-3, ...

A Former Brilliant Member - 3 years, 1 month ago

Ovidiu Dumitrescu
Feb 21, 2018

size = 52 #even
deck = *(1..size)
shuffle = deck.dup
shuffle2 =[]
n=0
loop do
    n+=1
    for i in 0..(size-1)
        shuffle2[2*i+1] = shuffle[i] if i<size/2
        shuffle2[2*(i-size/2)] = shuffle[i] if i>=size/2
    end
    shuffle = shuffle2.dup
    break if deck == shuffle
end
puts n

$\boxed{52}$

This is optimizable:

def cycleLength(n, L, deck):

    nn = n
    count = 0
    while True:
        nn = 2*nn % (L + 1)
        count += 1

        if nn in deck:
            deck.remove(nn)

        if nn == n:
            break

    return count

def findLongestCycle(deck):

    L = len(deck)
    maxShuff = 0
    while len(deck) > 0:
        card = deck.pop()
        count = cycleLength(card, L, deck)
        maxShuff = max(count, maxShuff)
        if len(deck) < maxShuff:
            break

    return maxShuff

n = 52
deck = range(1, n + 1)
print findLongestCycle(deck)

And Yag - 3 years, 3 months ago

Uros Stojkovic
Feb 21, 2018

import numpy as np

count = np.zeros((52))

for i in range(52):
    if (np.floor((i+1)/26 - 0.0001) % 2 == 0): #had to include -0.0001 to make program consistent for i = 25 and i = 51
        A = (2*(i+1)) % 52
    else:
        A = (2*(i+1)-1) % 52
    count[i] +=1

    if i+1 != 52:

        while (A != i+1):
            if (np.floor(A/26 - 0.0001) % 2 == 0):
                A = (2*A) % 52
                count[i] += 1
            else:
                A = (2*A-1) % 52
                count[i] += 1
    else:
        while (A != 0):
            if (np.floor(A/26 - 0.0001) % 2 == 0):
                A = (2*A) % 52
                count[i] += 1
            else:
                A = (2*A-1) % 52
                count[i] += 1

print(count)

Output:

[ 52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.
  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.
  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.  52.
  52.  52.  52.  52.  52.  52.  52.]

Arthur Wang
Feb 25, 2018

Python

  l = [i for i in range(52)]

  def s(l):
    p = []
    a = l[:len(l)/2]
    b = l[len(l)/2:]
    for i in range(len(l)/2):
      p.append(b[i])
      p.append(a[i])
    print p
    return p

  print l
  for i in range(1, 53):
    print i
    l = s(l)

Yuriy Kazakov
Feb 25, 2018

It is very fine rezult
A002326

Matthew Hellwig
Feb 24, 2018

The way I saw it, the first card has to travel down one side and back up the other, 26 times each way.

Tommy Hu
Feb 22, 2018

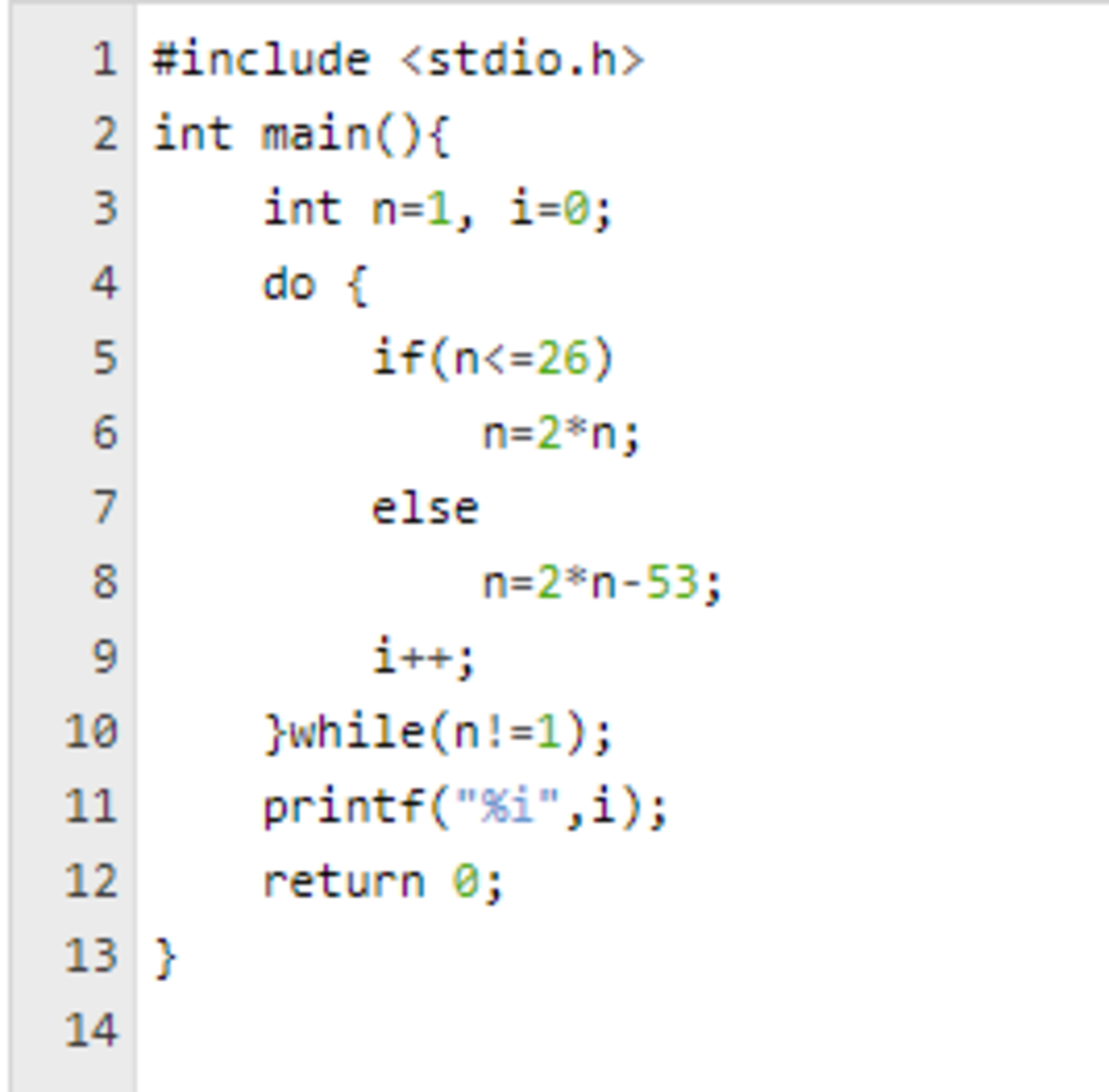
include<iostream>

define N 60

define M 52

using namespace std; int card[N],card1[N]; void change(int arry[]) { for(int i=1;i<=M/2;i++) { card1[2 i-1]=card[M/2+i]; card1[2 i]=card[i]; } for(int j=1;j<=M;j++) card[j]=card1[j]; } int main() { int cnt=0,flag=0; for(int i=1;i<=M;i++) card[i]=i; while(flag==0) { flag=1; change(card); cnt++; for(int i=0;i<=M;i++) if(card[i]!=i) { flag=0; break; }
} printf("%d\n",cnt); return 0; }

Zaldi Zaldivar
Feb 22, 2018

Output 52

Oscar Langarica
Feb 22, 2018

Solution in Microsoft Excel VBA

Sub shuffling_deck()

Dim list

Dim reference

Dim newarrangement

Count = 0

n = InputBox("Deck Size", "Magician's perfect shuffling")

ReDim list(1 To n)

ReDim reference(1 To n)

ReDim newarrangement(1 To n)

    For i = 1 To n
        list(i) = i
        reference(i) = i
    Next

equal = False

    Do While equal = False

        For i = 1 To n / 2
            newarrangement(2 * i - 1) = list(n / 2 + i)
            newarrangement(2 * i) = list(i)
        Next

        Count = Count + 1

        For i = 1 To n
            list(i) = newarrangement(i)
        Next

        equal = True

        For i = 1 To n
            If reference(i) = list(i) Then
            Else
                equal = False
                Exit For
            End If
        Next

    Loop

MsgBox (Count)

End Sub

Perfect In-Shuffles

The answer is 52.

10 solutions

include<iostream>

define N 60

define M 52

0 pending reports