Periodicity of a Block on a Ramp

Conservation of energy tells us that, when the particle is at the point $(x,x)$ , the particle has kinetic energy $8\dot{x}^2$ , and hence it follows that $8\dot{x}^2 + V(x) \; = \; V(2)$ where $V(x) \; = \; 4g\sqrt{2}x + 10\big[\sqrt{(x - 3)^2 + (x - 5)^2} - 1\big]^2$ is the total potential energy of the system.

When $g=0$ we find that $\dot{x}=0$ when $V(x) = V(2)$ , which occurs when $x = 2,6$ . Thus the particle oscillates between $x=2$ and $x=6$ with period $T_1 \; = \; 2\int_2^6 \frac{dx}{\dot{x}} \; = \; 4\sqrt{2}\int_2^6 \frac{dx}{\sqrt{V(2) - V(x)}} \; = \; 4.99869593...$ making $a=5$ .

On the other hand, when $g=10$ we find that $\dot{x}=0$ when $x = 2$ and $x= X = 1.90061716$ , so the particle oscillates between $x=2$ and $x=X$ with period $T_2 \; =\; 2\int_X^2 \frac{dx}{\dot{x}} \; = \; 4\sqrt{2}\int_X^2 \frac{dx}{\sqrt{V(2) - V(x)}} \; = \; 4.09792111...$ (not $4.060$ ) which makes $b=4$ . Thus the desired answer is $5 + 4 = \boxed{9}$ .

When $g=0$ , the starting point is the low point of the oscillation. When $g=10$ the starting point is the high point of the oscillation.

@Steven Chase , @Krishna Karthik

Without gravity, the block initially slides up the ramp. With gravity, the block initially slides down the ramp. So I had to use different loop termination conditions in each case. I resolved the spring force into a component parallel to the ramp, and a component normal to the ramp. Without gravity, the period is $\approx 4.999$ and with gravity, the period is $\approx 4.060$ .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98

import math
import numpy as np

#######################################

# Constants

xh = 3.0   # hinge coordinates
yh = 5.0

x0 = 2.0   # coordinates of start point
y0 = 2.0

theta = math.pi/4.0  # ramp angle

g = 10.0  # gravity

m = 8.0   # mass

k = 20.0  # spring constant
L0 = 1.0  # spring natural length

dt = 10.0**(-5.0)  # time step

u1x = -1.0/math.sqrt(2.0)  # unit vector down ramp
u1y = -1.0/math.sqrt(2.0)

u2x = -1.0/math.sqrt(2.0)  # unit vector normal to ramp
u2y = 1.0/math.sqrt(2.0)

#######################################

# Initialize simulation

t = 0.0
count = 0

D = 0.0  # distance from start point along ramp
Dd = 0.0
Ddd = 0.0

#######################################

while Ddd >= 0.0:     # loop condition with gravity (sliding down ramp initially)
#while Ddd <= 0.0:    # loop condition without gravity (sliding up ramp initially)

    D = D + Dd*dt     # numerical integration
    Dd = Dd + Ddd*dt

    x = x0 + D*u1x   # xy coordinates
    y = y0 + D*u1y

    Sx = xh - x     # vector from block to hinge
    Sy = yh - y

    S = math.hypot(Sx,Sy)   # spring length

    sx = Sx/S   # unit vector from block to hinge
    sy = Sy/S

    Fs = k*(S-L0) # spring force magnitude

    Fsx = Fs * sx  # spring force vector
    Fsy = Fs * sy

    # Resolve spring force into components down ramp and perpendicular to ramp

    # Fsx = F1*u1x + F2*u2x   
    # Fsy = F1*u1y + F2*u2y

    M11 = u1x
    M12 = u2x

    M21 = u1y
    M22 = u2y

    M =  np.array([[M11,M12],[M21,M22]])
    vec = np.array([Fsx,Fsy])

    Sol = np.linalg.solve(M, vec)

    F1 = Sol[0]
    F2 = Sol[1]

    Ddd = (m*g*math.sin(theta) + F1)/m  # acceleration of block along ramp

    t = t + dt
    count = count + 1

    #if count % 1000 == 0:
        #print t,D,Dd

 #######################################   

print ""
print ""  
print dt
print (4.0*t)

Goteeem.

I did a similar method to Steven. I wonder what @Mark Hennings would like to offer to this problem. He mostly attempts physics problems using pure mathematics.

Of course, to find the time period one would have to compute an integral.

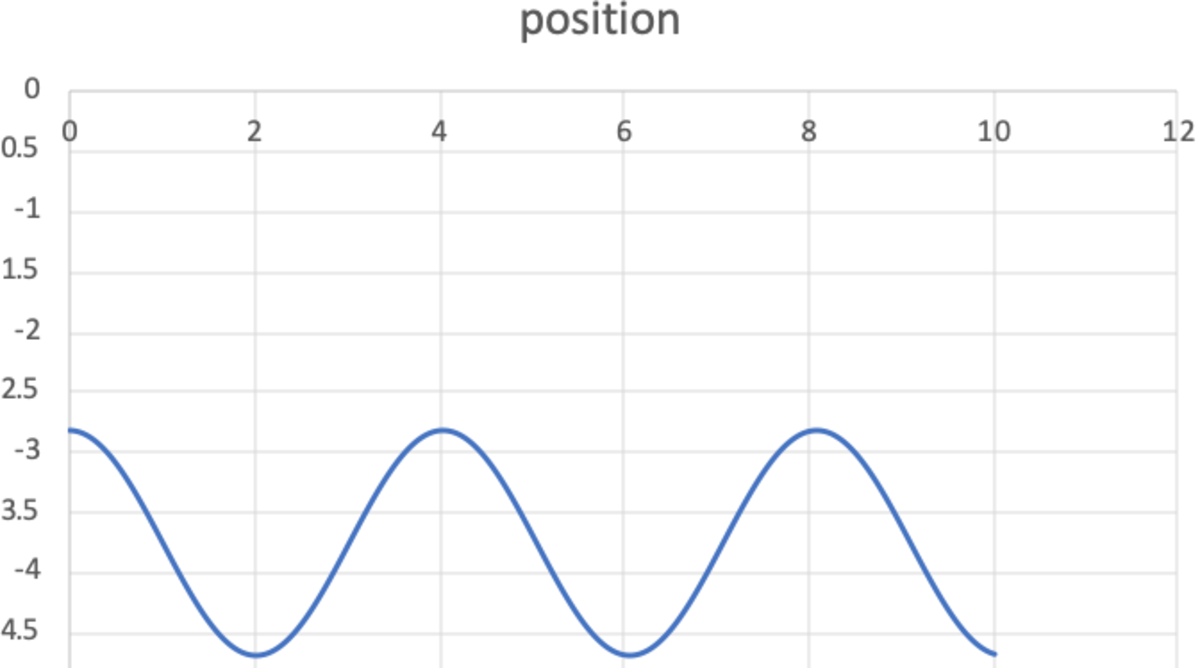
Here are two graphs showing the motion in the two cases:

g = 10

g = 0

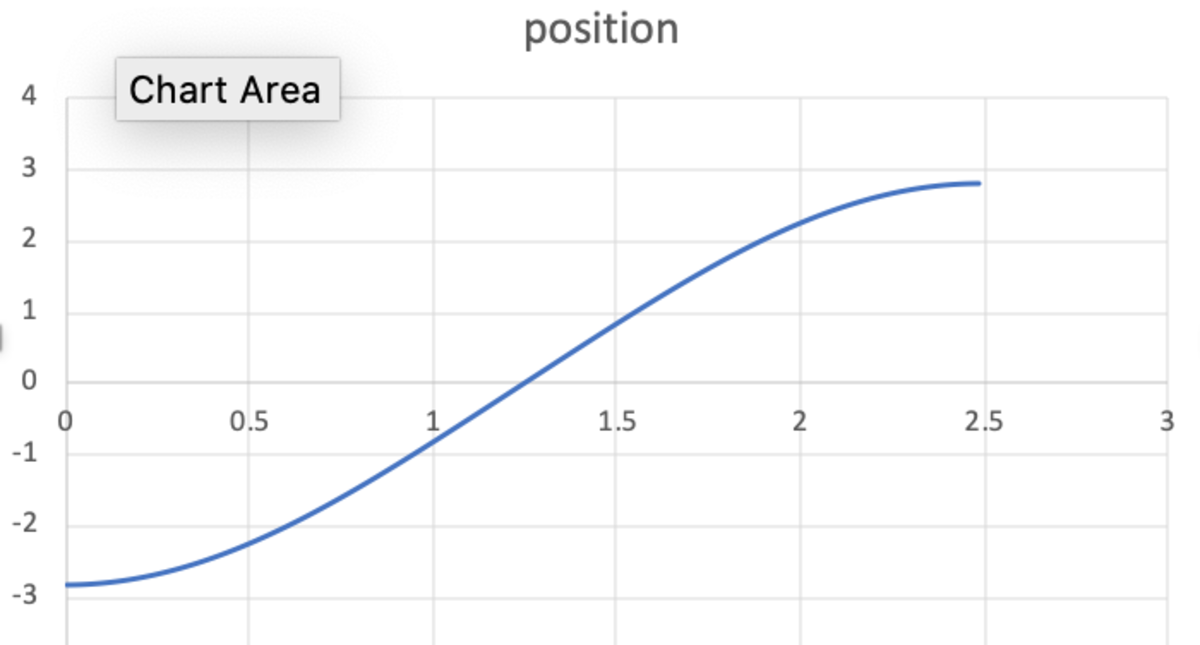
Without gravity, it is expected that the period is longer. This is due to less forces constantly opposing each other, because gravity is always opposing the spring force and slowing the oscillation. The block always stays below $(4, 4)$ with gravity, and without gravity it oscillates evenly between $(4, 4)$ in the positive and negative displacement from $(4, 4)$ .

One can imagine the "zero- $g$ " scenario to be just like a block oscillating on a horizontal surface in space. It simplifies things. Fun problem.