Perplexing Pyramid Problem

Let $a$ be the base side length and let $h$ be the height.

$S = V \\ a(a + \sqrt{a^2 + 4 h^2}) = \frac{1}{3} a^2 h \\ 3 a + 3 \sqrt{a^2 + 4 h^2} = a h \\ 3 \sqrt{a^2 + 4 h^2} = a h - 3a \\ 9 (a^2 + 4 h^2) = a^2 h^2 -6 a^2 h + 9a^2 \\ 36 h^2 = a^2 h^2 -6 a^2 h \\ a^2 = \frac{36 h^2}{h^2 - 6 h} = \frac{36 h}{h - 6 }$

Plugging back into the volume equation:

$V = \frac{1}{3} a^2 h = \frac{12 h^2}{h - 6}$

We are told that for a particular volume, there should only be one value of $h$ at which it occurs. This is equivalent to saying that the $h$ value should correspond to a local minimum or maximum of $V$ , when $V$ is plotted against $h$ .

$\frac{d}{dh} V = 0 \\ (h-6)(24 h) - 12 h^2 = 0 \\ 12 h^2 = 144 h \\ \boxed{h = 12}$

Let the $h$ be the height of the pyramid, $s$ be the slant height, $2x$ be the side of the square base, $V$ be the volume, and $S$ be the surface area.

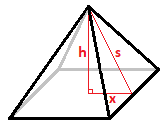
By Pythagorean's Theorem, $x^2 + h^2 = s^2$ , so $S = 4x^2 + 4x \sqrt{x^2 + h^2}$ and $V = \frac{1}{3}4x^2h$ . Since $S = V$ and $x = \sqrt{\frac{3V}{4h}}$ , substituting into $S$ we have $V = 4(\sqrt{\frac{3V}{4h}})^2 + 4\sqrt{\frac{3V}{4h}}\sqrt{(\sqrt{\frac{3V}{4h}})^2 + h^2}$ which simplifies to $12h^2 - Vh + 6V = 0$ (for $V > 0$ ), which by the quadratic equation solves to $h = \frac{V \pm \sqrt{V^2 - 288V}}{24}$ .

To be the only right pyramid to have that volume, the discriminant $V^2 - 288V = 0$ , which is at $V = 288$ (for $V > 0$ ), and this volume gives the pyramid a height of $h = \frac{288 \pm 0}{24} = \boxed{12}$ .