Perps in a Cyclic Quad

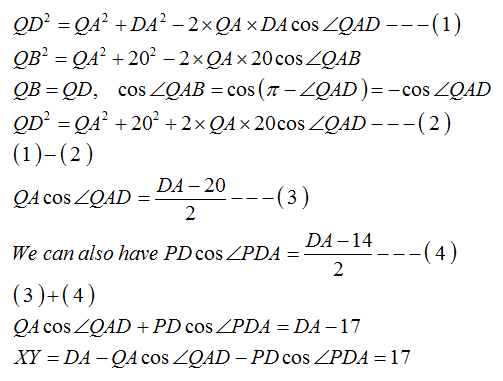
Locate the point $A'$ on line $AD$ such that $A'\ne A$ and $A'Y=AY$ .

Note that $QB=QD$ by definition.

Also, $\angle ABQ=\angle ADQ=\angle A'DQ$ .

Angle chasing more, we see that

$\begin{aligned} \angle QAB &= 180^{\circ}-\angle QDB \\ &=180^{\circ}-\angle QBD \\ &=180^{\circ}-\angle QAD\\ &=180^{\circ}-\angle QA'A \\ &= \angle QA'D \end{aligned}$

Thus, $\triangle QAB\sim \triangle QA'D$ by AA-similarity. However, $QB=QD$ so actually $\triangle QAB \cong \triangle QA'D$ .

Thus, $AB=A'D$ . Thus $DY = A'D+A'Y = AB+AY$

Similarly for the other side, we get that $AX=CD+DX$

Summing these two equations together, we get $AX+DY = AB+CD+AY+DX$

but $AX=AY+XY$ and $DY=DX+XY$ so the equation simplifies after cancellation into $2XY = AB+CD$

Plugging in values we know, $XY=\dfrac{20+14}{2}=\boxed{17}$ and we're done. $\Box$

Note the Red Herrings in this problem:

The length of $BC$

$BC\approx XY$

$PC \stackrel{\approx}{\parallel} BQ$

The distance in the AD direction between points P and Q is the same as the corresponding distance between points P' and Q' on the opposite side of the circle from them. The dimensions given do not determine the radius of the circle. If the distance sought is indeed independent of the radius of the circle, it has to work for any radius, specifically in the limit it has to work for the radius going to infinity. If all the distances - 20, 16, and 14 - are aligned on a straight line, point Q' is 1 left of point C and point P' is 2 left of point B. Distance P'Q' is then obviously 17.