Pi Day Ellipse

Let put the center of the square as the origin of the coordinate (x,y). The area of the ellips is πab = π, so ab = 1, ..... (1) the equation of the ellips is x^2/b^2 + y^2/a^2 = 1, ........... (2), and the equation of tangent is : x + y = √5/√2 . ............... (3) Substitute y = √5/√2 – x, and a = 1/b, to eqs.(2) (b^4 + 1) x^2 - √10 b^4 x + (5/2 b^4 - b^2) = 0. Discriminant of this quadratics eqs. D = 0, then 2 b^4 – 5 b^2 + 2 = 0, b= √2

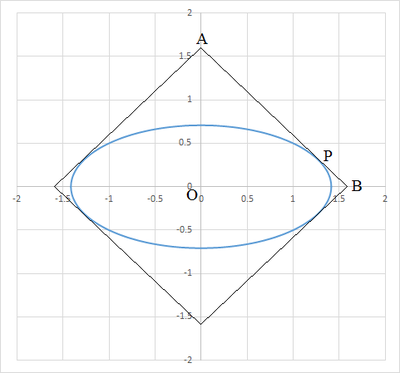
Let us rotate the square by $45^\circ$ , the center of the ellipse be the origin $O$ of the $xy$ -plane, the semi-major axis be $a$ and semi-minor axis be $b$ . Then the equation of the ellipse is $\dfrac {x^2}{a^2} + \dfrac {y^2}{b^2} = 1$ , where we can assign $x=a\cos \theta$ and $y=b\sin \theta$ . Since area of the ellipse is given by $\pi ab = \pi$ , $\implies b = \dfrac 1a$ .

Since the area of the square is $5$ , then its side length is $\sqrt 5$ and that of its diagonal is $\sqrt{10}$ . Let $P$ be the point where the side $AB$ is tangent to the ellipse. We note that the gradient of $AB$ is $-1$ and its equation is $y = \dfrac {\sqrt{10}}2 - x$ .

The gradient of the ellipse at point $P$ is $-1$ . Differentiating the equation of the ellipse, we have:

$\begin{aligned} \frac {2x}{a^2} + \frac {2y}{b^2} \color{#3D99F6} \frac {dy}{dx} & = 0 & \small \color{#3D99F6} \text{Note that }\frac {dy}{dx} = -1 \text{ at }P. \\ \frac x{a^2} & = \frac y{b^2} \\ \frac {\cos \theta}a & = \frac {\sin \theta}b \\ \implies \tan \theta & = \frac 1{a^2} & \small \color{#3D99F6} \implies \sin \theta = \frac 1{\sqrt{1+a^4}}, \ \cos \theta = \frac {a^2}{\sqrt{1+a^4}} \end{aligned}$

From

$\begin{aligned} y & = \frac {\sqrt{10}}2 - x \\ y + x & = \frac {\sqrt{10}}2 \\ \frac {\sin \theta}a + a \cos \theta & = \frac {\sqrt{10}}2 & \small \color{#3D99F6} \text{Multiply both sides by }a \\ \frac 1{\sqrt{1+a^4}} + \frac {a^4}{\sqrt{1+a^4}} & = \frac {\sqrt{10}}2a \\ \sqrt{1+a^4} & = \frac {\sqrt{10}}2a & \small \color{#3D99F6} \text{Squaring both sides} \\ 1+a^4 & = \frac 52 a^2 & \small \color{#3D99F6} \text{Rearranging} \\ 2a^4 - 5a^2 + 2 & = 0 \\ (2a^2 - 1)(a^2-2) & = 0 \end{aligned}$

$\implies \begin{cases} a = \sqrt 2 \\ b = \frac 1{\sqrt 2} \end{cases}$ , since $a > b$ .

Therefore, $p = \boxed 2$ .

Sorry I can't do the maths formulae nicely but..... Rotate the set-up till the semi-major axis is on the x-axis.

The ellipse has equation
p y^2 +x^2 / p = 1

And the top left side of the square y = x + sqrt (5) / 2

Now there must be ONE simultaneous solution so after reduction to one quadratic equation in x, the quadratic discriminant in terms of p must be zero.

I don't know how to write it....

It does work, I promise!

Since the area of an ellipse with a major axis $a$ and a minor axis $b$ is $A = \pi ab$ , and this ellipse has an area of $\pi$ , so $b = \frac{1}{a}$ . The equation of a vertical ellipse is $\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1$ , and if $b = \frac{1}{a}$ , this is equivalent to $a^4x^2 + y^2 = a^2$ .

Since the area of the square is $5$ , its sides are $\sqrt{5}$ . Let the square be centered at the origin. Then the sides of the square are on the lines $y = \pm \frac{\sqrt{5}}{2}$ and $x = \pm \frac{\sqrt{5}}{2}$ .

Rotating the ellipse $45°$ to align with the square’s diagonal gives a new equation $(a^4 + 1)x^2 + 2(1 - a^4)xy + (a^4 + 1)y^2 = 2a^2$ . Since the ellipse is tangent to the square, the discriminant must be zero at $y = \frac{\sqrt{5}}{2}$ , so $4(1 - a^4)(\frac{\sqrt{5}}{2})^2 - 4(a^4 + 1)((a^4 + 1) (\frac{\sqrt{5}}{2})^2 - 2a^2) = 0$ , whose largest solution is $a = \sqrt{2}$ , so $p = \boxed{2}$ .