Pillowed Diamond
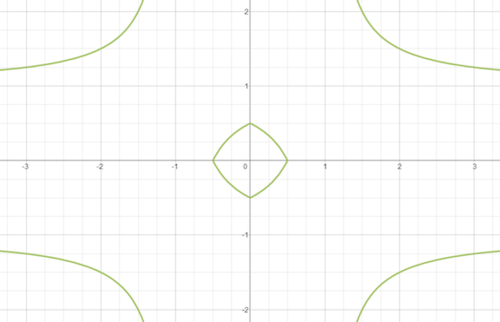 Above is the graph of the equation
∣
x
∣
+
∣
y
∣
−
∣
x
∣
∣
y
∣
=
0
.
5
Let the area of the
cute little pillowed diamond
in the middle be
A
. What is the value of
⌊
1
0
0
0
A
⌋
?
Above is the graph of the equation
∣
x
∣
+
∣
y
∣
−
∣
x
∣
∣
y
∣
=
0
.
5
Let the area of the
cute little pillowed diamond
in the middle be
A
. What is the value of
⌊
1
0
0
0
A
⌋
?
The answer is 613.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You have the right answer, but there's a mistake in the solution. When you make the u -substitution , saying this, 2 1 ∫ 0 0 . 5 x − 1 1 d x = ∫ 0 0 . 5 u 1 d x You are wrong because you forgot to adjust the bounds of the integral to 1 and 1 . 5 . Luckily, you resubstituted for u = x − 1 and then used the bounds of 0 and 0 . 5 .
Generalized, when making a u -substitution, if g ( x ) = u , ∫ f ( g ( x ) ) × g ′ ( x ) d x = ∫ f ( u ) d u ∫ a b f ( g ( x ) ) × g ′ ( x ) d x = ∫ g ( a ) g ( b ) f ( u ) d u
Log in to reply
Ah shoot, thanks for correcting me. Fixed.
Log in to reply
No problem!
To be honest, I was a little surprised when you put x − 1 back in for the substitution. You could have just evaluated it at the u stage.
It's a lot easier to find ∫ 2 9 u d u than ∫ 0 1 x 4 − 2 x 3 + 8 x + 2 4 x 3 − 6 x 2 + 8 d x
Log in to reply
@Trevor B. – The reason I didn't just evaluate it is because I am a total noob at Calculus :P
Log in to reply
@Daniel Liu – Oops, I made a mistake myself. What I should have said was that it is harder to find ln ( x 4 − 2 x 3 + 8 x + 2 ) ∣ ∣ 0 1
Oops half the solution is missing. In the process of fixing it right now...
Done. Also, did I overrate the difficulty of this problem? Seeing that the little fine loops is level 3, then this should be level 2 or 1. Oops? Well I guess free extra rating for everyone... ⌣ ¨
Log in to reply
it got so hard that this happened: I multiplied by 5 and I divided by yⁿ. then. I needed to add x. Then I multiplied by ∞. So. 0 + 0 ÷ x² = d dx.
You can also be clever by working in the first quadrant therefore eliminating need for absolute value. Reaarange equation and integrate. Then times the quarter by 4. :)
Log in to reply
If you read my solution, that is exactly what I did. ;)
I have a doubt. |y| = 0.5 - |X|/ 1- |X|
For the region of the pillowed diamond to the left hand part of the x-axis |X| = -X & |Y| = Y Shouldn't the equation become y = 0.5 - (-X)/ 1 - (-x) => 0.5+x/1+x ?
Area under the curve=4*integral of the limits between 0-0.5....not just one times ,since its a diamond shape,for all four quadrants,we need to find the area for all the four quadrants
I answered 614 first because 1000A is 613,7...., so if you ask me you have cut the round off to early.
I too answered 614 please set both the answers to be correct
Because working with absolute values is hard, let us confine our working space to non-negative x and y . This way, we can get rid of the absolute values and find the area of one fourth of the pillowed diamond, then multiply by 4 to find the total area.
Since x , y > 0 , our equation simplifies to x + y − x y = 0 . 5 .
Factoring y out gives x + y ( 1 − x ) = 0 . 5 .
Now we can isolate y and create a function of x : y = 1 − x 0 . 5 − x
This can be simplified to y = 2 x − 2 1 + 1
Now that we have found our bounding equation for the top right side of the pillowed diamond, we can take the integral if the equation to ind the area underneath it.
First, we must find the upper and lower bound. The lower bound is obviously 0 . The upper bound occurs when y = 0 , which gives ∣ x ∣ = 0 . 5 . Since we are only considering positive x , the upper bound is 0 . 5 .
Thus, we want to find the value of ∫ 0 0 . 5 2 x − 2 1 + 1 d x
First, we can divide it into two sections: ∫ 0 0 . 5 1 d x + ∫ 0 0 . 5 2 x − 2 1 d x which simplifies into x + 2 1 ∫ 0 0 . 5 x − 1 1 d x
Substituting u = x − 1 (which means d u = d x ) we simplify it into x + 2 1 ∫ 1 1 . 5 u 1 d u
This is simply x + 2 1 ( ln ∣ u ∣ ) ∣ ∣ ∣ ∣ 1 1 . 5 which becomes x + 2 1 ( ln ∣ x − 1 ∣ ) ∣ ∣ ∣ ∣ 0 0 . 5
This evaluates as ( 2 1 + 2 1 ( ln 2 1 ) ) − ( 0 + 2 1 ( ln 1 ) ) = 2 1 − 2 1 ln 2
This is the area of a quadrant of the pillowed diamond. The area of the entire diamond is thus 4 ( 2 1 − 2 1 ln 2 ) = 2 − 2 ln 2 ≈ 0 . 6 1 3 and our answer is 6 1 3 .