7 Piece Pizza
What's the minimum number of straight cuts required to cut a pizza into 7 pieces of equal area?
Details and Assumptions:
- A straight cut may start and end anywhere on the pizza—not just on the circumference.
- The pizza comes uncut and round in the box.
- You cannot take the pizza out of the box or move any part of it.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
What do you mean by uniquely determines the unequal areas of regions?
Log in to reply
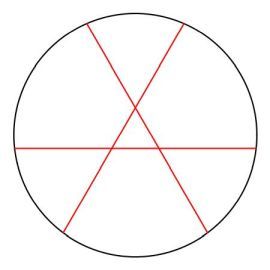
If we start with cuts that divide the pizza into areas of ratio 7 3 , 7 4 , then making 3 such cuts at 6 0 degrees apart will establish that the pizza is divided into 7 pieces of unequal areas. Let's look at it another way: The first chord cut has 1 degree of freedom, the next two chord cuts have 2 degrees of freedom each, making it 5 degrees of freedom. But there are 7 regions such cuts must divide the pizza into, which means after choosing the areas of 5 regions, the last two are determined.
Log in to reply
Oh, I think I start to understand. By the way, could you explain a little bit more about degree of freedom because I don't really get it? Thanks a lot in advance.
Log in to reply
@Donglin Loo – I'll give you an easy example: Let's say that I want to find a , b such that
a
+
b
=
3
a
2
+
b
2
=
5
a
3
+
b
3
=
7
Does there exist a , b that can meet the condtions? No, because each a , b has one degree of freedom, making it a total of 2 degrees of freedom in which to determine 3 outcomes. We can find a , b that will meet any two of the condtions, but not all three. it's a very useful concept in solving problems with many variables. If there are n degrees of freedom to determine n outcomes, then usually there is a finite number of solutions. If there's fewer, then usually no solution is possible. If greater, then usually there's infinitely many solutions possible. Check out solving Systems of inear equations as one application where it talks about this.
I say, "usually", because sometimes there are degeneracies or constraints, it isn't always so simple. It depends on the problem.
Log in to reply
@Michael Mendrin – Oh I totally get it, Thanks for that detailed explanation. @Michael Mendrin
nice. you have given a proof using intermediate value theorem that such a cut exists. but we need to do lot of calculations to find out how to cut the pieces as all the pieces have same area. something which blocked me from reaching the solution is i was always thinking the cuts should be chords of the circle. thanks for the nice solution. this problem is funny because you want to do this without opening the box.
a bit unfair if you ask me, all should get the same amount of crust (jk)
The question didnt specify if you had to use the whole pizza just 7 equal slices. I can do it in one continuous looping slice with each person receiving a circle. The problem stated a straight cut must go from side to side but did not exclude any other type of cut. Thus my solution of one looping cut is the least.
This is not "Advanced" level. It fits the second level.
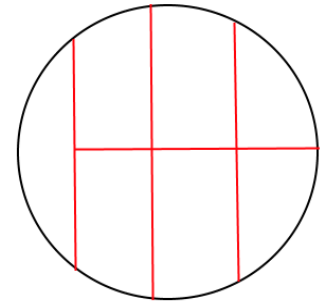
A vertical line to cut 1/7 of the pizza (on the left). Another vertical line to cut 2/7 of the pizza (on the right).
A vertical cut to divide the center piece in half.
At last a horizontal line passing thru the center of the pizza to divide in half the three pieces on the right.
Hey, that works too!
Same solution as me. Good job!
This was the solution I arrived at as well, though I think Michael's diagram is a bit more elegant.
This qustion is easy to solve by only analysing the least number of straight cut to devide pizza into 7 piece. The equal area is not that important since you can always find a good way to slightly adjast the cut and gain equal area.
I can make 7 slices with three cuts
Log in to reply
7 equal slices?
Can you please show how?
Lol guess who guessed correctly
"easy to solve"
No - you cannot always find a way to adjust the cut to gain equal areas if you have only used the minimum number of cuts to divide the pizza into 7 pieces. That number is 3, and Michael Mendrin's answer above explains why a solution with 3 cuts is impossible.
Not only you got the minumun cuts to divde it into 7 pieces wrong (the ans which is 3), you wrongly assume you can always adjust the area with said number of cuts so all areas are the same, and thus wrongly assume it to be the same solution as this question. You just had a lucky strike through wrong assumptions.
The answer of 4 is wrong, it can be done with 3 lines unless I am missing something
You can cut the pizza into 7 pieces with 3 straight cuts. It's just that you can't make them all equal.
It is not possible for 3 cuts to divide the pizza into 7 regions of equal areas, as that would require 3 chords each having an area of 7 3 of the whole pizza cutting each other into thirds, or 6 pieces with a crust and 1 in the center. For reasons of symmetry, the chords will have to be at 6 0 degrees apart, which uniquely determines the unequal areas of the regions, as the following figure shows.