Planet 9 From Outer Space
8 points with integer coordinates are located on a 8 × 8 lattice
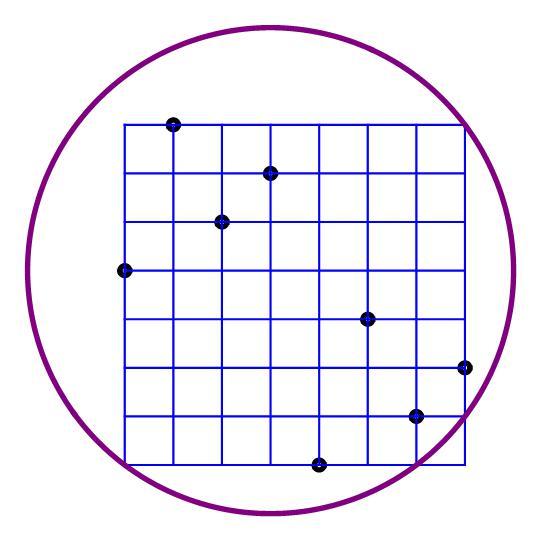
such that the sum of the squares of all 28 distances between each pair of them is 1216. There exists a locus of a 9 th point such that the sum of the squares of all the distances between it and each of the 8 points on the lattice is 800. This locus is a circle. Find the radius of that circle.
Note: The graphic posted does not show actual locations of points or circle or radius.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I like your "physics" solution! I wonder if it has any applicability in classical mechanics, though?
n 1 i ∑ r i 2 should be 2 n 2 n − 1 i ∑ r i 2 . It still cancels out in the end though, so it doesn't really matter
Log in to reply
Not really-- on the second line of that set of equations, I replaced the sum over i , j < i by half of the sum over i , j , thus smuggling in the "diagonal" entries for which i = j . This does not change the sum because these entries contribute zeroes anyway.
In the last step, I split the sum ∑ i , j r i 2 + r j 2 = n ∑ i r i 2 + n ∑ j r j 2 = 2 n ∑ i r i 2 .
how does this math work even know i'm a little bit smart
Here's one solution, showing the locations of the 8 points such that the sum of squares of the 2 8 distances is 1 2 1 6 , and showing the locus of the 9 th point which is a circle of radius 9 , and such that the sum of the squares of the distances from any point on it to each of the 8 points on the lattice is 8 0 0 . The radius is independent of the locations of the 8 points provided the sum of the squares of the 2 8 distances is 1 2 1 6 .
However, one need not even determine the locations of the 8 points on the lattice to find R . Let n be the number of points, T be the sum of the squares of the distances of each of the 2 1 n ( n − 1 ) pairs of points, S be the sum of the squares of the distances from any point on the locus to each of the n points on the lattice, and let R be the radius of the locus which is always a circle. Then the following relation holds
n S = n 2 R 2 + T
Thus, for n = 8 , S = 8 0 0 , R = 9 , T = 1 2 1 6 , we have
8 ⋅ 8 0 0 = 6 4 ⋅ 8 1 + 1 2 1 6 = 6 4 0 0
The algebra works out as follows, where ( x , y ) is the coordinate of any point on the locus, and ( x i , y i ) the coordinates of the n points.
n S = n ( i = 1 ∑ n ( x i − x ) 2 + i = 1 ∑ n ( y i − y ) 2 )
n 2 R 2 = n 2 ⎝ ⎛ ( x − n 1 i = 1 ∑ n x i ) 2 + ( y − n 1 i = 1 ∑ n y i ) 2 ⎠ ⎞
T = 2 1 ( i = 1 ∑ n j = 1 ∑ n ( x i − x j ) 2 + i = 1 ∑ n j = 1 ∑ n ( y i − y j ) 2 )
From these, it can be determined that for any n the relation holds, as all the variables drop out.
Note that the center of the circle locus is the centroid of the n points.
Very interesting question again. I was expecting all points to be on a circle and thought of this post . In fact this would work for eight points on a circle of radius 1 9 forming regular octagon. They would not have integer coordinates though. The points in the configuration in your solution are placed symmetrically on three concentric circles with weighted squared radius average of 1 9 .
Log in to reply
The relation described in my solution works for n points in general. The only reason why I discussed 8 points in a 8 × 8 lattice is to make people work to find which ones will have the sum of 1 2 1 6 for the 2 8 squares of distances--even though it was never necessary to do so. I'll have to look at that note you've linked and see what bearing this relation has in the special case of regular polygons of n vertices.
It is not fair to give a task without necessity solving the cernel problem which is in this case finding the location of the 8 points. Achieving this (= a bit difficult) it is then easy to calculate the equation of the circle via quadratic addition. Furthermore it is not so clear that the middle point of the circle is identical the centroid of the 8 points. Who says this, God? Do you have some connection?
Log in to reply
People have a choice of how to solve this problem. One way would be to find an arrangement of 8 points that meets the criteria, from which the radius of the "orbit" of the 9th point can be determined. The other way is to look for a general relation that avoids having to find any such arrangements. Arjen Vreugdenhil has posted an excellent solution using that other approach.
This problem only asks for the radius of the "orbit" circle of the 9th point.
The center of the "orbit" circle is indeed always at the centroid of any number of arbitrary points on the plane. It just works out that way, and Arjen has explained this very well.
Log in to reply
Yes, thank you! But the bottom line is: A far-fetched problem!
Log in to reply
@Andreas Wendler – Well, you know, the title, "Planet 9 from Outer Space", which is rip-off of a famous "bad" 1959 sci-fi movie Plan 9 from Outer Space That should have been a hint. Read where it says in the Wikipedia that it was "..the worst film in the history of cinema".
It works for this configuration of points as well.

Distance between two points can be seen as result of addition of two vectors which have common center of all circles as one endpoint. Sum of squares of distances works out as sum of radii of circles giving the value of 1216. The weighted squared radii average for 3 circles is ( 2 ∗ 2 4 . 5 + 4 ∗ 1 8 . 5 + 2 ∗ 1 4 . 5 ) / 8 = 1 9 ,
The radius of the circle for the 9th point can be calculated as 8 0 0 / 8 − 1 9 = 9 .
This is more irregular configuration with center of mass having integer coordinates.

This kind of opens up another kind of problem, which is about finding which arrays of n points yields the same sum. I hadn't thought much about it until just now. Your take on this is interesting. I wonder if this has applicability in number theory?
In the question it is written integral coordinates but the middle point in your solution is not an integral coordinate
Log in to reply
So? The radius is still 9, which the question was asking for.
The fact that the coordinates are integral is irrelevant to the relation, which holds for arbitrary reals.
n S = n 2 R 2 + T
It is not included in 8 points in question, just center of the circle. I should have marked it differently, so it is not confusing.
A physics approach: work with vectors, and make a good choice of coordinates.
Let n = 8 be the number of points, with coordinates r i . Without loss of generality we can choose the origin of our coordinate system lies at the center of mass, so that ∑ r i = 0 .
Let n 2 D the sum of squares of distances between the points. (We choose n 2 because we expect this sum to increase quadratically in the number of points.) We can write D = n 2 1 i ∑ j < i ∑ ∣ r i − r j ∣ 2 = 2 n 2 1 i ∑ j ∑ ( r i 2 + r j 2 − 2 ( r i ⋅ r j ) ) = n 1 i ∑ r i 2 . (The sum of the dot product r i ⋅ r j equals zero because of our assumption about the coordinate system.)
We add a new point at position p . Let n E be the sum of squares of distances between this point and the other points. Then E = n 1 i ∑ ∣ r i − p ∣ 2 = n 1 i ∑ r i 2 + p 2 . (Again, the mixed products r i ⋅ p add up to zero.)
Subtracting the equation for D from the equation for E , we obtain E − D = ( n 1 i ∑ r i 2 + p 2 ) − ( n 1 i ∑ r i 2 ) = p 2 . It follows that the position of the new point, p , satisfies the equation p 2 = E − D , in other words, it lies anywhere on a circle around the origin (= center of mass of the original points) with radius R = E − D . Plugging in the given values we have D = 8 2 1 2 1 6 = 1 9 , E = 8 8 0 0 = 1 0 0 , R = 1 0 0 − 1 9 = 9 .