Playing with rods and sticks

We have two rods A B and C D touching each other and placed on the ground in the position as shown in the figure. At t = 0 the system is set free to move, find the normal force (in Newtons) between the two rods at this instant.
Details and Assumptions
- Mass of rod A B = 3 5 3 kg , mass of rod C D = 2 6 3 kg, θ = 3 0 ∘ .
- There is no friction between the ground and the rod and also there is no friction between the two rods, (In the diagram it may seem that the rods are stuck to the ground but it's not so, they can freely slip on the ground)
- The ends of both the rods are perfectly curved and assume they are perfectly rigid and very thin.
- Rod A B is perpendicular to C D (i.e ∠ A D C = 9 0 ∘ ) and rod C D touches rod A B at its mid-point(i.e A D = D B )
- g = 1 0 m/s 2
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yeah ! It takes time because I generalise This Question ,And Good Problem Ronak ! Slight Variation Can be done in it By Putting Sufficient Friction between Two rods ! I have Analysed This too , Will You Guys Too analyse it ? So That We Can Create this question's Part 2 !
@Ronak agarwal @Mvs Saketh
Log in to reply
Is this is not big enough for you, you want friction in there as well? :P
Log in to reply
Ha! Ha! Ha! , I formed 9 equations in 9 variables and solved to get the answer to this question, and posted the beautiful equation below.
By the Way putting sufficient friction in the doesn't make it any more harder , but putting insufficient friction makes this a freak.
I Spent almost hour To analyse Both Cases ! (including the case when we can use IAOR or not) And I think it is not as much Long Since We can use Some Fact's from this question's ! Did you Dare to analyse it ? What did you Think about that ? :)
Log in to reply
@Deepanshu Gupta – Thanks for giving the idea, but can you please give me the priviledge of making part 2 of this question.
Log in to reply
@Ronak Agarwal – Sorry For Late Response , I was Busy in Preparing for My Sunday Review Test . And Yes Ronak It is Your Patent :) .
And Also Ronak Congratulation For Selecting in Chemistry Olympiad Stage-1 (\ddot\smily) Today I read in Newspaper That You got Selected in it , Great , Once Again Congo Bro :D
And In That Question I Think We have already 9 equation's and We have one more Variable that is : friction , Then We Can Simply Use The Constrained that "Net Relative acceleration along common Tangent is also zero " . So we have 10 equation and 10 variable which can be solved easily (Not So But Yet It can be :D)
And Saketh No I want to say That I checked whether we can use ICR or not , But instead I have Lot of Doubt's in it ! when Sufficient friction is present b/w rods ! when I'am Trying To use IAOR then I got Some Doubt's Can You guys Please clear that ? @Ronak Agarwal @Mvs Saketh
Doubt's :

1) What is ICR of this System ? Since There is Two Point of intersection of Perpendicular Velocity and If we Consider P as ICR then Velocity of 'C' is not not Permissible , And Similarly for 'Q' .
Note : Here I Used Fact That there is No Horizontal Force on System of Combined Both rods , So velocity of System Should be in vertical Direction only !
2)- Does it is Possible That Any Rigid Body doesn't have any ICR ?
3) - How You Defined an Rigid Body ?
4)- why This Question is Shows Flag ?
Note : (Here I assumed Combination of Two rods as Rigid Body Because There is no relative Motion b/w Point of Contact Since There is Sufficient Friction ( which We already assumed it) )
Log in to reply
@Deepanshu Gupta – Yep the seperation between two points , like take the distance between foot of both the rods,, it is changeing,, so the system aint a rigid body, also the w need not be same for both rods, let alone the individuals IAOR, , but yes to apply no slipping, u can apply the fact that relative acceleration along common tangent is 0, which easily gives another constraint, so we have ax1, ay1, ax2,ay2 , f, N , R1, R2, alpha 1, alpha 2, as 10 varriables and also 10 equations , for the instant immediately after, for any later instant, we need ofcourse to use conservation of energy, but that would become way more clumsy, But think if friction is insufficient, then too its not so hard, because it means maximum friction acts, and if we know coefficient of friction, its a piece of cake, we got 9 varriables 9 eqn just like original problem, but in any later instant, if we want to calculate, then we cant use energy conservation because there will be heat dissipation, then we will be done with , because we will need to find out how far the friction point has travelled,
@Deepanshu Gupta – Can you please review my problem @Deepanshu Gupta and remove it's flag
Log in to reply
@Ronak Agarwal – I reviewed it , But it Still Shows error ! I Think we should call @Calvin Lin Sir !
@Deepanshu Gupta – Ans to 3)We define a rigid body in very simple terms, that is it is a body in which velocity of seperation between any two points is zero.
Ans to 1)Also the system you took can't be considered a rigid body. Hence ICR of your system is not defined.
Ans to 2) If a rigid body is not rotating then is not having an unique ICR.
Ans to 4) Well someone reported it by saying that please specify the units in which you want the answer, I was extremely angry at this thing and my problem got unneccasarily flagged.
Log in to reply
@Ronak Agarwal – I agreed with This Explanation ! But What Can You Say About This Question ( when friction is present b/w Cylinders ) Ignore what is written on Image ( Consider friction only b/w cylinders) Click here
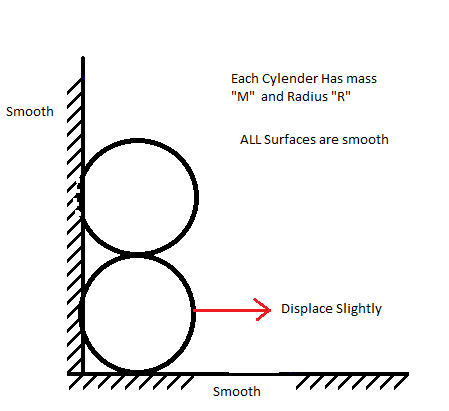
Log in to reply
@Deepanshu Gupta – Here because there is no slipping and because, u showed in ur other post that both have same w, and also because the centre of mass of two cylinders is always at their contact point, and the contact point is clearly constrained to move in a circle till in any loss of contact occurs with wall so , u can give an ICAR to the COM of the system
@Deepanshu Gupta – I didnt think about it actually, as for IAOR, having only one constraint makes it hard to locate the point, but if you managed to solve that way, do share your method
Beautiful problem! Did the same way! (+1)
I am giving only formula for calculating N in terms of m A B , m C D , θ
N = m A B ( 1 + 3 c o s 2 θ ) ( 4 s i n 2 θ ) + m B C ( 1 + 3 s i n 2 θ ) ( 1 + 2 c o s 2 θ ) 3 ( m A B m C D ) ( g ) ( c o s θ ) ( c o s 2 θ )
i'm back , why still show my name as brilliant member ;p ?
Actually , problem is simpler than it looks, i really thank you for giving good angles and for connecting the rods normally that too at mid point,,
and i must say, how did you know that all those weird numbers would add up to finally give such a simple integer result, it was hard to expect, and at the end i see them cancel out so fine,
ok so heres my way, a bit hectic though, and i will just drop in the equations and the reasons, solve them yourself, , (dont worry its simple to solve them, just dont make calculation mistakes)
ok, consider first rod,, the forces on it are
1) Mg 2) normal reaction of rod acting perpendicularly upon it at midpoint 3) ground reaction
and torque is only provided by ground reaction obviously,
so let the centre of mass move right with a1 and down with a2 as acceleration and let rod rotate about it with acceleration alpha,
also note that its end touching ground has no vertical acceleration,
Now equations concerned are
M g − N c o s ( x ) − R = m a 2 R c o s ( x ) 2 l = I α N s i n ( x ) = m a 1 2 α l c o s ( x ) = a 2
Now these effectively yield two equations that we will use later (basically since i dont give a shit about ground reaction, i eliminate that, also i express angular accelration in terms of a2)
Note that R is ground reaction, N is what we want,
m g − N c o s ( x ) = 9 1 3 m a 2 N s i n ( x ) = m a 1
Now note that i have skipped some steps and input some angle values,
Now similarly solving for second rod yields me the two effective equations
N c o s ( x ) + M g = 3 7 M b 2 N s i n ( x ) = M b 1
Where b1 is acceleration of com of 2nd rod (right side one) along x and b2 along y,,
Now focus, this is the real thing,, since the rods are in contact, and it has been very intelligently mentioned that the ends of the rod are smooth and curved, so at all instants i can draw a common normal at the contact point and obviously they must have similar accelerations along normal, so we have
a 2 c o s ( x ) − a 1 s i n ( x ) = b 1 s i n ( x ) + b 2 c o s ( x )
Now input the values of a1 a2 b1 b2 which i have given and isolate N, and finally everything messy cancels out to yield 9g,
It should have been mentioned to take g as 10m/s^2 btw
answer is 90N,
Nice problem,