Playing with the Glome
2 x y + 4 y z + 6 z w
Let M be the maximum of the expression above if x 2 + y 2 + z 2 + w 2 = 1 , where x , y , z and w are real numbers. Write M = p + q for two positive integers p and q , and enter p + q .
Bonus question : For a x y + b y z + c z w , with the same constraint, express the maximum M in terms of a , b and c .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, exactly! Very nice exposition! That's what I had in mind (+1).
Just a small detail to show that I have read your work: There are some square roots missing where you should have ± 7 ± 4 0
Log in to reply
Thanks for spotting the typo. Correction made.
Log in to reply
Oh you're back to Brilliant? My favorite user is back!!!! YIPEEE! Let's celebrate!
So by your Spectral Theorem ,
min ( 2 x y + 4 y z + 6 z w ) max ( 2 x y + 4 y z + 6 z w ) = − 5 − 2 5 + 2 = − 1
Right?
Log in to reply
Right!
The Spectral Theorem is a general result from Functional Analysis. In a very special case (finite-dimensional and real) it gives us the SED (symmetric eigenvalue decomposition) that Dr. Hennings explained so well: For any symmetric matrix A there exists an orthogonal matrix S such that S − 1 A S = S T A S is diagonal.
The SED implies that the maximum and minimum of q on unit vectors are the largest and smallest eigenvalues, respectively.
In this example, we could conclude that min ( q ) max ( q ) = − 1 without any computation, of course, just by switching two signs, x and z , say.
Log in to reply
@Otto Bretscher – .
The Spectral Theorem is a general result from Functional Analysis. In a very special case (finite-dimensional and real) it gives us the SED (symmetric eigenvalue decomposition)...
I'm already lost here. Haha. Anyway thanks for your reply! Comrade Otto
Log in to reply
@Pi Han Goh – Just start reading at "SED" then, Comrade... ;)
There is a complex version of this... just replace "symmetric" by "Hermitian" and "orthogonal" by "unitary"
Log in to reply
@Otto Bretscher – Is this problem solvable by quadratic forms?
Edit: Wait. Nevermind... there's a x y z term.
Log in to reply
@Pi Han Goh – No, this is definitely not a quadratic form... not a single quadratic term! It looks like the kind of contrived problem that would have been created for the sole purpose of amusing the fans of classic inequalities.
Quadratic forms (as well as the closely related bilinear forms) are so important, among other things, because they are linked to the geometry of space: length, angles, distance, etc., that can be expressed in terms of inner products.
To both Comrade Otto and Mr @Mark Hennings , I have some inquiries:
Question 1 : We must find convert the constraint to the sum of squares of variables = 1 first right? That is, if x 2 + y 2 + z 2 + w 2 = 2 , then we must first make the substitution of x = 2 X , y = 2 Y , z = 2 Z , w = 2 W . And if the answer is yes, why is it so? And does this method extends any number of variables (in this problem, there's 4 variables)?
Question 2
:
(a) So if I change the expression from
(
2
x
y
+
4
y
z
+
6
z
w
)
to
(
2
x
y
+
2
x
z
+
2
x
w
+
2
y
z
+
2
y
w
+
2
z
w
)
, then the matrix is:
A = ⎝ ⎜ ⎜ ⎛ 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 ⎠ ⎟ ⎟ ⎞
Right?
(b) With det ( λ I − A ) = 0 , we get λ is equal to the roots to the equation x 4 − 6 x 2 − 8 x − 3 = ( x − 3 ) ( x + 1 ) 3 = 0 right?
(c) And thus the maximum value for this new expression is 3 and the minimum value is -1 right?
Question 3 : Why must the matrix be symmetric? Is there a theoretical reason for it?
Question 4 : What does it mean if the characteristic polynomial have no real roots? Or is it impossible to occur? If it can occur, does it mean the expression has no max/min value? Is there any significance for non-real eigenvalues?
Question 5 : If the characteristic polynomial only has 1 distinct root? Does that mean that it is equal to the maximum and/or minimum value of the expression? Or is it impossible to occur?
Question 6 : How do you construct an expression like 2 x y + 4 y z + 6 z w such that the eigenvalues are "nice" values like 5 + 2 ? This time, the matrix MUST be symmetric.
Log in to reply
Any quadratic form q ( x 1 , x 2 , … , x n ) = 1 ≤ i , j ≤ n ∑ a i j x i x j can be written in the form x T A x where x = ( x 1 x 2 ⋯ x n ) T and A is a n × n real symmetric matrix. The matrix A need not be symmetric, but it always can be, and there is a rich theory of symmetric matrices which we are using.
To be specific, for any real symmetric n × n matrix A there is associated an orthonormal basis of eigenvectors. In particular, the characteristic polynomial of A factorizes completely over the reals. This is equivalent to saying that there exists an orthogonal matrix P such that P A P T is diagonal. Thus, if we change variables by setting X = P x then the quadratic form becomes λ 1 X 1 2 + λ 2 X 2 2 + ⋯ + λ n X n 2 where λ 1 , λ 2 , … , λ n are the diagonal entries of P A P T . Since, moreover, X 1 2 + X 2 2 + ⋯ + X n 2 = x 1 2 + x 2 2 + ⋯ + x n 2 (because P is orthogonal), maximizing/minimizing q ( x ) over the unit hypersphere is just a matter of maximizing/minimizing λ 1 X 1 2 + λ 2 X 2 2 + ⋯ + λ n X n 2 over the same unit hypersphere. It is easy to see that the result is just the largest/smallest eigenvalue of A .
To answer one of your particular questions, if a symmetric matric has a single eigenvalue, then P A P T is a multiple of the identity matrix, and hence A is a multiple of the identity matrix.
To find particular quadratic form with particular eigenvalues, start with the diagonal matrix that you want (pick the eigenvalues that you would like, say 5 + 2 , 5 − 2 and 3 ), and play around with a choice of orthogonal matrix P .
To learn the theory of all this, you need to check out books on Linear Algebra and on bilinear forms in particular.
Log in to reply
Thank you for your detailed answer. Your explanation via hypersphere really nails it! Some follow up questions:
Question 7 :
The matrix A need not be symmetric, but it always can be...
Can you give me an explicit example? Are you just performing some row operations? Or is there something more specific/in depth knowledge to it?
Question 8 :
To find particular quadratic form with particular eigenvalues, start with the diagonal matrix that you want (pick the eigenvalues that you would like, say 5 + 2 , 5 − 2 and 3 ), and play around with a choice of orthogonal matrix P .
Can you explain what "play around" means in this context?
Once again, thank you for being so patient in explaining all these to me. I learned some linear algebra in college via brainwashing, so I don't know what I'm actually learning. I think I only remembered what Gram Schmidt algorithm is for.
- BIGGEST FAN!!!!
Log in to reply
@Pi Han Goh – to Question 7: The construction of the symmetric matrix A of a quadratic form is straightforward: Make a k k the coefficient of x k 2 and a i j = a j i half the coefficient of x i x j .
to Question 8 (we discussed this issue before): If you have a diagonal matrix D and you want a symmetric matrix A whose eigenvalues are the diagonal entries of D , compute A = S − 1 D S = S T D S for any orthogonal matrix S .
Log in to reply
@Otto Bretscher – This sounds too easy to be true. Let me peruse it a few more times.
Log in to reply
@Pi Han Goh – Easy indeed... nobody said this stuff was hard.
@Pi Han Goh – The result we are using is elegant and easy to apply, with implications that are very simply expressed. The theory, while involved, is also very elegant. The ability to diagonalize matrices, as we do here, is an important weapon in the Linear Analyst's arsenal. That symmetric matrices are diagonalizable has many applications; the existence of principal modes of oscillation about a point of stable equilibrium in mechanics problems, and the existence of energy levels in quantum mechanics are (basically) two of them!
Log in to reply
@Mark Hennings – Wow! You really do know everything! Thanks for the conversation!
Wow, I see that while I was sleeping you guys had a wonderful discussion on quadratic forms. Thank you so much for this lucid explanation, Dr. Hennings.
Can you show us that the maximum is attained?
Log in to reply
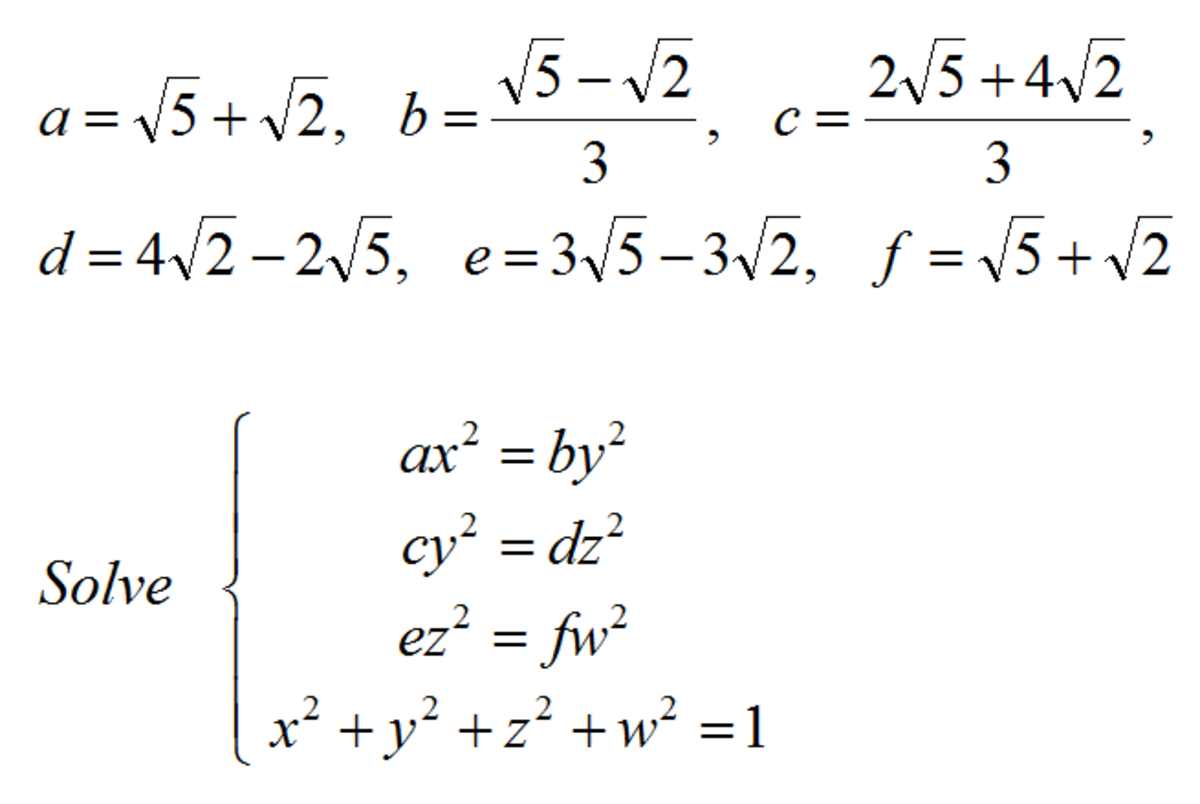
Log in to reply
Yes, that will work, but the solution involves some pretty tedious computations (finding a , b , c , d , e , f ). This seems like an interesting alternative, but Dr. Hennings' solution is more direct and general. Mathematically, solving your six equations is equivalent to finding the roots of the characteristic polynomial.
Log in to reply
@Otto Bretscher – Yes! Dr. Hennings' solution is more direct and general. But how to get the value of x, y, z, w when the maximum occur?
Log in to reply
@汶良 林 – The maximum of the quadratic form is attained at the two unit eigenvectors associated with the maximum eigenvalue λ = 2 + 5 . To find these eigenvectors, solve the linear system A v = λ v , a quick and routine task. One eigenvector is v = ( 6 , 6 λ , 3 λ 2 − 3 , λ 3 − 5 λ ) ... now normalize.
Log in to reply
@Otto Bretscher – Thank you very much!
Log in to reply
@汶良 林 – I thank you for your solution! It is good to see that, with great effort, this problem can be solved with algebra alone (in the old sense of "algebra": solving equations)

The maximum of the quadratic form 2 x y + 4 y z + 6 z w subject to the constraint x 2 + y 2 + z 2 + w 2 = 1 is, as usual, the maximum eigenvalue of the symmetric matrix defining the quadratic form. In this case the matrix is A = ⎝ ⎜ ⎜ ⎛ 0 1 0 0 1 0 2 0 0 2 0 3 0 0 3 0 ⎠ ⎟ ⎟ ⎞ The characteristic polynomial of this matrix is d e t ( λ I − A ) = λ 4 − 1 4 λ 2 + 9 = ( λ 2 − 7 ) 2 − 4 0 and so the eigenvalues of the matrix are ± 7 + 4 0 = ± ( 5 + 2 ) ± 7 − 4 0 = ± ( 5 − 2 ) Thus M = 5 + 2 , so the answer is 7 .
In general, repeating these calculations for the matrix B = ⎝ ⎜ ⎜ ⎛ 0 a / 2 0 0 a / 2 0 b / 2 0 0 b / 2 0 c / 2 0 0 c / 2 0 ⎠ ⎟ ⎟ ⎞ yields the characteristic polynomial λ 4 − 4 1 ( a 2 + b 2 + c 2 ) + 1 6 1 a 2 c 2 = ( λ 2 − 8 1 ( a 2 + b 2 + c 2 ) ) 2 − 6 4 1 ( ( a + c ) 2 + b 2 ) ( ( a − c ) 2 + b 2 ) so that the largest eigenvalue is ( 8 1 ( a 2 + b 2 + c 2 ) + 8 1 ( ( a + c ) 2 + b 2 ) ( ( a − c ) 2 + b 2 ) ) 2 1 . After some algebra, this can be shown to to equal to 4 1 [ ( a + c ) 2 + b 2 + ( a − c ) 2 + b 2 ] .