One left, one right

Probability Level 1

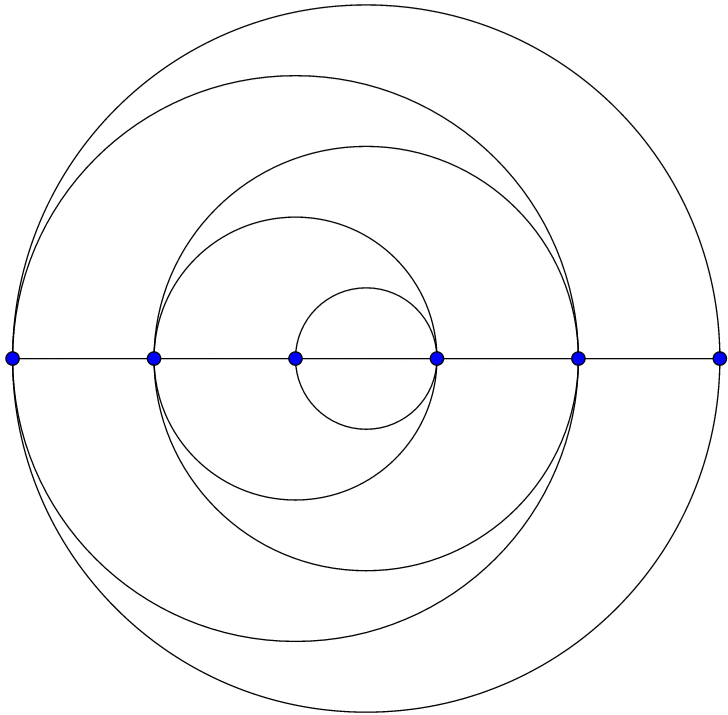
Find the total number of semicircles in the given figure.

The answer is 10.

1 solution

Ashish Menon
Apr 19, 2016

In the upper half of the figure, there are $5$ semicircles.
In the lower half of the figure, there are $5$ semicircles.
So, totally, there are $\boxed{10}$ semicircles in the given figure.

Abhay Tiwari - 5 years, 1 month ago

Hmm.. I didnt get your question properly, are not infinitely many shapes possible, by moving the squares one inc further then another inch, then another inch . Seems like a great question to me ;)

Ashish Menon - 5 years, 1 month ago

Ashish, I have made the correction, thanks a lot. I was thinking from my side and from the solver's side. You can check it now. :)

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – It was my pleasure, seriously te question is cool, I am still figuring out how the answer is more than 2 XD.

Ashish Menon - 5 years, 1 month ago

@Ashish Menon – Swapnil,

a small version of this question.

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – Swapnil? Or Ashish :P

Ashish Menon - 5 years, 1 month ago

@Ashish Menon – Sorry i am getting mixed up here, I was responding to his problem simultaneously. Any ways, do check it. :P ;)

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – Are we allowed to use different combinations of squares to obtain the same pattern like putting green above red above black, and the red above black above green.

Ashish Menon - 5 years, 1 month ago

@Ashish Menon – Yes you can do as you like, You have to make one and only one combination by which maximum squares can be drawn out.

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – I understand the question now and I think I get the proper figure in my mind too, I try will solve it rigt away.

Ashish Menon - 5 years, 1 month ago