Points On A Circle
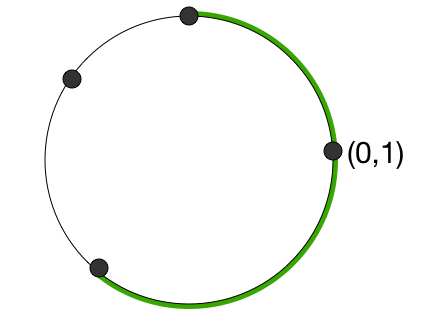
Consider the unit circle
x
2
+
y
2
=
1
.
Choose 3 points uniformly at random on the circumference, which divides the circle into 3 arcs.
What is the expected length of the arc that contains the point ( 1 , 0 ) ?
Technical details: We pick a point on the circumference uniformly at random in the following manner.
1. First select
θ
∼
U
[
0
,
1
]
, the uniform distribution on the unit interval
2. Next, we pick the point
p
=
(
cos
(
2
π
θ
)
,
sin
(
2
π
θ
)
)
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The reason why we can't just take the average is that these lengths are not independent (?)
Log in to reply
Not quite. Even though it is true that the lengths are not independent, however the linearity of expectation still applies to the result.
Think about the "2 arc" case. What is the probability that the point is in the shorter arc? Is it going to be 2 1 ?
"Choose 3 points randomly on the circumference." Problems like this one have at their root the difficulty that "choose three points randomly on the circumference" is not a clearly-defined procedure. There are multiple different ways of defining this, and hence your answer can very well depend on which definition of this procedure you chose to adopt. I have seen this corundum demonstrated in several different kinds of geometrical problems like this one, and you just have to look them up in the right library or the right Web page.
Log in to reply
Technically yes, that in order to choose randomly, we need to specify what the actual "random" approach is.
Because we are essentially in 1-D, I have let that slide. Let me clarify that in the question.
Note that this isn't the reason for why we can't just take the average.
Log in to reply
There is a physical reason why the expected value of that arc [containing the point (1, 0)] is so large. Note that it is pi rather than (2/3)pi. Repeating the experiment many times, no matter how you do it, in a significant number of cases all three points will be in the left half-plane (e.g. on the left half of the circle, or in Quadrants II and III). All of these cases contribute an arc length of greater than pi to the solution. However, there are other cases in which the arc length is less than pi. When you work out the details, the expected value works out to be exactly pi.
Log in to reply
@Dale Wood – There is a slightly different problem. Forget about the specified point (1, 0), and just work out the expected value of the length of ANY of the three arcs. I haven't worked out the details, but I think that this answer will work out to be 2pi/3 from sheer symmetry. Frequently, some of the arcs can be much shorter than 2pi/3, but then there are many arcs that are longer than 2pi/3. I would work out the details but it is getting quite late where I live.
Log in to reply
@Dale Wood – Now, let (a, b) be ANY point on the circle, and not just (1, 0), and its central angle is "ohm". From the previous results, we can find that E[L | ohm] = [the expected value of L given ohm], which is the same as [the expected value of L given (a, b)] = 2pi/3. Next, we can average over all possible values of ohm, assuming that this is uniformly distributed: f(ohm) = 1/(2pi) over the 2pi length of the circle. We integrate: E(L) = Integral of E[L | ohm] f(ohm)d(ohm) = (2pi/3)(1/2pi)(2pi) = 2pi/3. By the arbitrariness of (a, b) and "ohm", this is expected value of ANY of the three arcs that you care to choose.
Log in to reply
@Dale Wood – There are probably other ways of solving the problem if you don't know the concept of conditional expectation, yet. This is one that comes in handy in simplifying the math of many expectation problems.
@Dale Wood – Great! That's indeed the reason why the first solution is wrong.
To put it mathematically, the probability that the point lies within a line segment is proportional to the length of the segment (divided by the circumference). Longer line segments are much more likely to contain the point, than are shorter line segments. As such, we are not just looking for E ( l 1 ) , but more like E ( l 1 2 ) (possibly with some scaling factor), where we also account for the likelihood that the point lies in the line segment. As Dale elaborates, calculating E ( l 1 ) gives the expected length of any segment, and not the segment containing the point.
The good answer is 2*pi/3 An'y thing else is wrong.
"It doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong. Richard P. Feynman"
Log in to reply
Substantiate your reasoning. What is the series of steps that you made?
Read Dale's comments. How do they relate to your steps?
Since you mentioned Richard Feynman's comment, have you done up the monte-carlo simulation of these values? If so, please share the data, and we can verify if the answer is indeed 2 pi / 3.
Log in to reply
Yes, you are right. The answer is pi/2.
To who come by here and thing the answer is 2*pi/3 as I wrongly thought at a certain moment: CHANGE YOUR MIND. I tested it in many different ways and gave always pi/2.
I put this citation again. But this time to myself : "doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong. Richard P. Feynman"
Log in to reply
@N S – I believe most people would make that similar misconception. Do you understand why your initial reasoning is incorrect? If so, how would you explain the error to convince someone to "change your mind"?
Log in to reply
@Calvin Lin – Yes. First thing I did was to calculate the probability in a completely different way.
Take three points x y and z on a circle of perimeter 1. Each point is represented by it's arc length starting from the origin O For the 3 points x y and z the arc length around the origin O equals 1 - 0.25 ( 2|y-x| + |(2 z -y-x- |y-x|) | + |(2*z -y-x+|y-x|)| ) Now just use wolfram to integrate it over x y and z and see the result =0.5
Integral 1- (2 abs(y-x)+abs ( 2 z -y-x-abs(y-x) )+abs ( 2*z -y-x+abs(y-x) )) /4 dx dy dz, x from 0 to 1,y from 0 to 1, z from 0 to 1
@Calvin Lin – Easy way to solve the problem. Let S (0,1) our origin point. Let A B and C the 3 random points on the circle.
The 4 points A B C and S will form respectively 4 arcs of lengths L1 L2 L3 and L4. E(L1)+(EL2)+EL(3)+EL(4)=2*pi
So each expected arc length is pi/2 and the expected length of the arc the point S (0,1) is pi
In the general case: if we have n random points the expected arc length around the point S (0) = 4*pi/(n+1)
Log in to reply
@N S – I disagree that is an easy way. While it gives the correct numerical answer, it doesn't have proper substantiation. In particular, you made the assumption that E ( L 1 ) = E ( L 2 ) = … = E ( L n ) , which does not seem justified to me.
Log in to reply
@Calvin Lin – Yes it is. Just think of it like this: fix the origin point then chose n points randomly. Then ask someone else who doesn' know your origin point to descripe the circle, he will see 12 random points.
Any way, I already did the experience and tested it. Up to you this time to make your integrals in the general case and come to the same result.
Log in to reply
@N S – I am not disagreeing with the final result.
I am merely pointing out that even though it might seem like an intuitive approach, if it doesn't have a proper reasoning/explanation, then it could still be wrong. For example, take your initial comment of "The good answer is 2*pi/3. Any thing else is wrong.", which is an intuitive approach that most people would have taken. As it turns out, it is not correct, for a subtle reason.
Log in to reply
@Calvin Lin – That's another story. My first answer matchs the case of a total number of 3 points. I missed taking the origin point in consideration.
So to justify things for you take these 2 similar problems : ●Chose one random point, make it you origin, then chose n other random points. ●chose n+1 random points.
It is clear that the relations between the points are the same.
Log in to reply
@N S – Great! That is the line of reasoning to explain the intuition. It can be rigorized by conditioning on configurations of points, to show why "when we include the 'origin' as a point, these n+1 line segments would have the same expected length".
Log in to reply
@Calvin Lin – Now, will you accept to change the beginning of your answer where you say that the 2pi/3 is wrong.
Both answers are good.
Read my last comments to see more explanation why both are good.
Log in to reply
@N S – No. Clearly, distinct answers cannot both be correct. At most one of them is correct.
The error with your reasoning is in the line "Then you say the origin will be on one of these arcs, thus the answer will be 2 pi / 3". See Dale's comment for why this is wrong. In particular, you are not properly accounting for the probability that a point lies within a line segment, which is proportional to the length of the segment, and not constant across different line segments.
The "origin point" doesn't matter. The expected length of the arc that contains any specific point on the circumference is π .
Log in to reply
@Calvin Lin – I read all the comments before starting the discussion with you.
Not 2 different answers for the same problem. BUT 2 different approachs of understanding this problem.
I am properly accounting for the probability.
Suppose that we forget about the origin point tel we mention it again later: Are the three arcs similar? what is the expected arc length?? Is it 2*pi/3 or No??? Now that we have 3 similar expected arc lengths, the probability that a certain point is on one arc of them is the same. Because all 3 arcs have same expected length.
Thus the origin point will be on an arc of 2pi/3 expected length.
@N S – I come back to clarify why many people did the mistake and answered 2*pi/3
In this question the rule of the origin point is not clearly defined. Thus there is 2 ways to see things:
■ you do the expected arc length between the 3 points witch gives 2 pi/3. Then you say the origin will be on one of these arcs. Thus the answer will be 2 pi/3
■the way to do this problem is to consider from the beginning the origin point as one of the other points and the expected arc length in this case is pi/2. Then at the end you merge the 2 arcs around the origin point. Thus the final result is pi/2
I hope now it's clear to everyone.
By the way, both answers are good for me when things are clearly described.
@Calvin Lin – I also did the integration way and gave same results. but I prefer the simplest solution.
Easy way to solve the problem. Let S (0,1) our origin point. Let A B and C the 3 random points on the circle.
The 4 points A B C and S will form respectively 4 arcs of lengths L1 L2 L3 and L4. E(L1)+(EL2)+EL(3)+EL(4)=2*pi/4
So the expected length of the arc around the point S (0,1) is pi
In the general case: if we have n random points the expected arc length around the point S (0) = 4*pi/(n+1)
Log in to reply
Rectification The 4 points A B C and S will form respectively 4 arcs of lengths L1 L2 L3 and L4. E(L1)+(EL2)+EL(3)+EL(4)=2*pi So each expected arc length is pi/2 and the expected length of the arc around the point S (0,1) is pi
In the general case: if we have n random points the expected arc length around the point S (0) = 4*pi/(n+1)
Solution is wrong. Simple empirical observation based on Technical Details implies all three points lie above or on x-axis which means arc between furthest points will always contain point (1,0) and thus expected length in this case will always include bottom semi-circle. Expected Length>pi P( no point chosen in [0,x] out of [0,pi] )=(1-x/pi)^3 On Solving rigorously, we get E(L)=E(Lc) + E(Lac)+ pi = pi/4 + pi /4 + pi = 3pi/2
Calvin's solution emphasizes the important concept of inspection paradox . Nevertheless, here is an alternative, less mysterious solution.
Let the independent random variables Θ 1 , Θ 2 , Θ 3 denote the polar angles of three randomly chosen points on the unit circle, where Θ i ∼ uniform ( 0 , 2 π ) . . Also. let M = max i Θ i and S = min i Θ i . Clearly, the length of the arc containing the point ( 1 , 0 ) is simply L = 2 π − ( M − S ) . Hence, E L = 2 π − E M + E S Now for any 0 ≤ x ≤ 2 π , due to the independence of the chosen points, we have: P ( M ≤ x ) = i = 1 ∏ 3 P ( Θ i ≤ x ) = ( 2 π x ) 3 Similarly, P ( S ≥ x ) = i = 1 ∏ 3 P ( Θ i ≥ x ) = ( 1 − 2 π x ) 3
Now use the fact that for any positive random variable Z , we can write E Z = ∫ 0 ∞ P ( Z ≥ t ) d t and evaluate the expectations. The answer turns out to be π .
Oh I didn't realize it had a name. Hm, let me read up on Renewal Theory .
Or we could determine that the joint probability distribution function for S and M is f S , M ( s , m ) = { 4 π 3 3 ( m − s ) 0 0 ≤ s ≤ m ≤ 2 π otherwise Integrating this over a suitable trapezoidal region gives P [ M − S ≤ t ] = 4 π 3 t 2 ( 3 π − t ) 0 ≤ t ≤ 2 π so that M − S has probability density function f M − S ( t ) = { 4 π 3 3 t ( 2 π − t ) 0 0 ≤ t ≤ 2 π otherwise leading to E [ M − S ] = ∫ 0 2 π t f M − S ( t ) d t = π It is interesting to note that the distribution of M − S is symmetric about π .
The following solution is wrong . Can you spot the mistake?
Do you know the reason why we can't just take the average? If no, see Dale's "There is a physical reason ..." comment below!
Now, for the correct solution:
Let's find the length of the "clockwise arc" from the point ( 1 , 0 ) . For a unit circle, the arc length is equal to the central angle. Since we have 3 points, thus
P ( L c ≥ x ) = P ( θ ≥ x ) = P ( no point chosen with angle in [0,x) out of [ 0 , 2 π ) ) = ( 1 − 2 π x ) 3
Then, we can calculate that the expected value is
E ( L c ) = ∫ 0 2 π ( 1 − 2 π x ) 3 d x = 2 π
We also have to account for the counter-clockwise arc, and it is clear that E ( L c l o c k w i s e ) = E ( L c o u n t e r c l o c k w i s e ) .
Hence, by linearity of expectation, E ( L ) = E ( L c l o c k w i s e ) + E ( L c o u n t e r c l o c k w i s e ) = π !
Note: The expected value calculation of E ( L ) = E ( θ ) = ∫ x P ( θ = x ) d x = ∫ P ( θ ≥ x ) d x follows by integration by parts . I am using the later integral, which isn't the standard formula used when doing an expected value calculation. This is sometimes called the Law Of The Unconscious Statistician .
Of course, if you do not trust it, you can calculate P ( L = x ) and then do the usual integral.