Points On The Plane, Are Scarier Than Snakes
 6 points are on the plane such that any 2 points are at most distance 2 apart. What is the most number of pairs of points which are strictly greater than
2
apart?
6 points are on the plane such that any 2 points are at most distance 2 apart. What is the most number of pairs of points which are strictly greater than
2
apart?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
In fact, the restriction of the points having distance > 2 can be further restricted to ≥ 2 without the answer changing. Consider an equilateral triangle with side length 2 and two points at each vertex.
Yeah...I think that holds true...
I think there must be an easier solution ...I'd love to see that ;)
Another easy construction of 12 pairs of points, is to take an equilaterial triangle of side length 2, and another set of points that are very close to those vertices.
Your idea in Doodling with points is close to the an important step of my proof. Show that: Given 4 points on the plane, let the maximum distance between 2 points (out of the 4) be M and the minimum distance between 2 points (out of the 4) be m , then m M ≥ 2 .
But Sir how can we put a condition on the minimum distance between two points ???
In the configuration where the 4 points form a square of side length 1 , then the minimum distance between 2 points is 1 and the maximum distance between 2 points is 2 , and we have m M = 2 .
@Calvin Lin – But I think that's a specific case....please can you elaborate a little more....
@Eddie The Head – Ah, I thought you were confused about what the statement meant, and was explaining why there is a minimum distance.
With regards to proving this fact, have fun with it!
@Calvin Lin – But sir it is given that the maximum distance between two points is at most 2.We have to find the configuration in which most number of points are s q r t 2 apart....SO how can we conclude something by taking side length 1 ???
I'm a bit confused about the statement.... :p ..Pleasee help!!
That was my exact solution also.
Why dont we use a hexagon with 1 unit side .. it satisfies all conditions also all diagnols are greater than root 2 ?
We will approach this problem using the following lemmas:
Lemma 1: Given 4 points on the plane, let the maximum distance between 2 points be M and the minimum distance between 2 points be m , then m M ≥ 2 .
Lemma 2: Given a graph with 6 vertices which are connected by 13 edges, there must be a complete graph on 4 vertices.
Then, given these lemmas, for the original set of 6 points, draw an edge in if the length is more than 2 . If there are at least 13 edges, then by Lemma 2, there exist 4 points each of which are distance 2 apart. By Lemma 1, the maximal distance would be greater than 2 × 2 = 2 , which contradicts the assumptions. Hence, there are at most 12 such pairs.
It remains to show that 12 is possible. Let A B C be an equilateral triangle of edge length 2. Take A 1 , B 1 , C 1 just within the triangle, and close to the respective vertices. This gives us 3 × 4 × 2 ÷ 2 = 1 2 edges with length close to 2. Hence we are done.
Proof of Lemma 1: We break into cases depending on the number of points in the convex hull.
If the convex hull consists of 2 points, then we have a straight line. The shortest distance is hence at most 3 1 of the longest distance (the entire line).
If the convex hull consist of 3 points, then we can show that m M ≥ 3 . Let O be the point contained within the convex hull. Then we can find a triangle where ∠ A O B ≥ 1 2 0 ∘ . WLOG, let O A ≥ O B , so ∠ O A B ≤ 3 0 ∘ . Then O B A B = sin ∠ O A B sin ∠ A O B ≥ sin ∠ O A B sin ( 2 ∠ O A B ) ≥ 2 cos ∠ O A B ≥ 2 ⋅ 2 3 = 3 .
If the convex hull consists of 4 points, then one of the angles is at least 9 0 ∘ . Let it be ∠ A B C . Let A B ≥ B C , so ∠ B A C ≤ 4 5 ∘ . Then, B C A C = sin ∠ B A C sin ∠ A B C ≥ sin ∠ B A C sin ( 2 ∠ B A C ) = 2 cos ∠ B A C ≥ 2 cos 4 5 ∘ = 2 .
Proof of Lemma 2: Since there are at most ( 2 6 ) = 1 5 edges, there are 2 edges that are not connected. If these 2 edges share a common vertex V, then any 4 of the other points will work. If the 2 edges do not share a common vertex, take 1 vertex from each of these pairs, and the other 2 vertices.
Okay...understood sir!!
May I ask, what role in the proof does the case of convex hull with 3 points play?
It ensures that we cover all possible cases.
Technically, I should include the case where the convex hull is 2 points (i.e the 4 points form a line), which I'd now edit in.
I see...thanks.
We know that the maximum distance between two pints in a square is along it's diagonal.So for the constraints given in the problem to hold it is essential that the given points should lie inside a square of side length 2 and diagonal length = 2 .
1. Let us first partition this square into 4 parts as show in the figure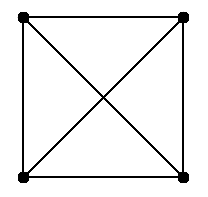 img
So from this figure it is evident that there can be at most 4 points such that the pairwise distance between each of them is is at least
2
.This clearly follows from the pigeonhole principle.
img
So from this figure it is evident that there can be at most 4 points such that the pairwise distance between each of them is is at least
2
.This clearly follows from the pigeonhole principle.
2. If such a construction is possible then since the distance between any 2 sides is 2 we must have a construction like this figure :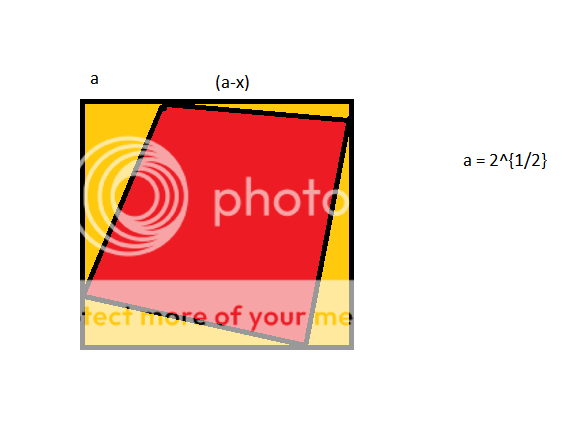 img
img
where x and 2 − x is taken as shown. By the Pythogorean theorem we have x 2 + ( 2 − x ) 2 = 2 2 x 2 + 2 − 2 2 x = 2 2 x 2 − 2 2 x = 0 x = ( 2 ) or x = 0 . According to our case the distance between the points should be greater than s q r t 2 so 4 points cannot be obtained. SO at most 3 points can be put in the region with pairwise distance > 2 .
Such a construction is easily possible by taking the points as close to the vertices as possible.
3. Now we can choose the other 3 points as close as possible(infinitesimally close-how about that??) to the initial 3 points in which case we will again have another triplet of points such that their pairwise distance is strictly greater than 2 .
So clearly from the diagram it is evident that only 3 pairs of points have distance < 2 and hence this is optimal.
The total number of pairs of points = 15.
So the greatest number pairs of points having distance > 2 is 1 2 .