Polygon Mystery
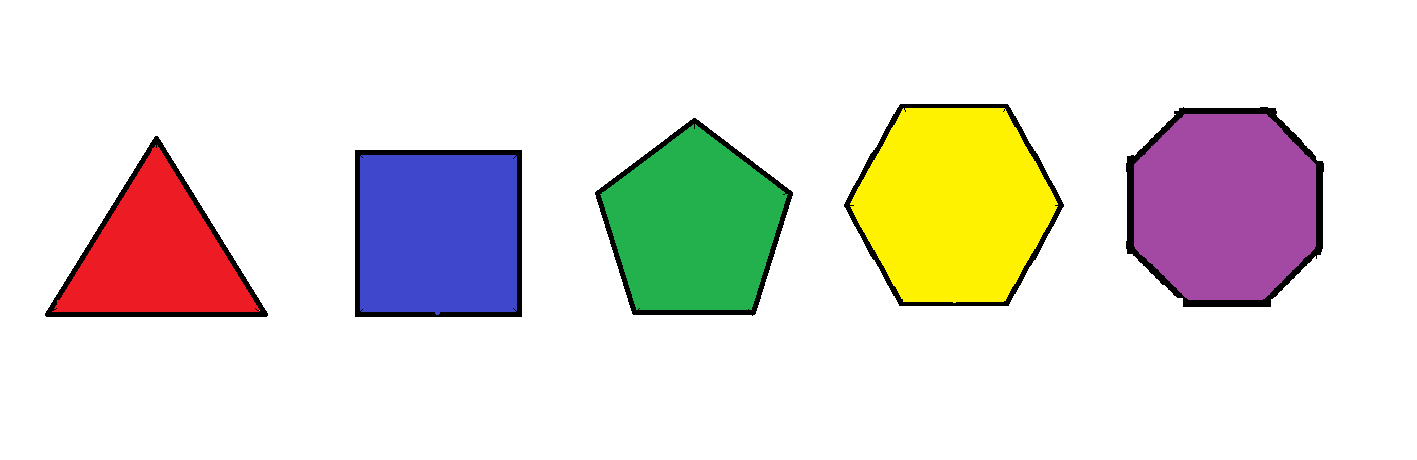
Which of the following regular polygons can be folded into a regular pyramid without cutting or overlapping any area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Why cant a square make a pyramid too ? It can make a square-based pyramid. Anyone mind giving me a better insight? With Thanks.
For completeness, you should explain why a similar folding doesn't work. For example, if we used a square and tried to fold it naively via the midpoints of the sides, then the "apex" of the pyramid would be the midpoint of the square, hence we get a 2-D figure instead of a 3-D figure.
However, it is not apparent to me that there isn't a "smart" way to fold it to obtain a pyramid (of some different base).
I'm sorry, but the solution is not complete without mentioning both square and triangle as correct answers. I did the following to make a triangular pyramid of a square.
Suppose the verteces of the square are A,B,C, and D. Make a point E as the midpoint of side AB. make a point F as the midpoint of side DA. The base of the pyramid is the triangle ECF. Points A, B and D meet as a new vertex above triangle ECF. (Works with a simple post-it note!) It is not a regular pyramid, but it satisfies the problem as a valid solution.
Log in to reply
It should be noted that @Worranat Pakornrat changed the question subsequent to this report. "Pyramid" has been changed to "regular pyramid," so that the square solution no longer applies to the new problem.
Log in to reply
Thanks. Those who previously answered square have been marked correct.
It is still not apparent to me that there isn't a "smart" way to fold the other figures to obtain a regular pyramid.
Log in to reply
@Calvin Lin – I suppose the answer lies in the edges that must be partitioned, and the prohibition against overlap. The square and the hexagon can easily make regular pyramids of zero height: the square by folding midpoints, the hexagon by folding alternating verteces.
Furthermore, the hexagon can be folded into a regular tetrahedron just like the triangle, since creating a zero-height pyramid results in a folded triangle. But the overlapping prohibition invalidates that solution. (For that matter, a regular triangle can likely be inscribed into any regular polygon.)
Of the regular shapes presented, only the triangle makes a non-overlapping regular tetrahedron, and the square makes the irregular tetrahedron given in my 'post-it note' solution. The non-overlapping requisite means that any edge partitioned must match equally against another edge, as a mismatch would result in what the problem describes as "a cut or overlap." Unless...
If "unused" flaps are permitted, it could be as you say: "smart" ways to fold a pyramid, albeit with uncut and unoverlapped flaps. I've just folded a triangular pyramid of small-but-positive volume out of a PENTAGON by inscribing an isosceles triangle against its vertex. It leaves two flaps, but they are neither cut nor overlapped.
Log in to reply
@Joel Nye – Nice analysis into this area. The ability to "fold across multiple vertices" makes it harder to analyze the general case.
Amazing how an innocent question like this leads to many more avenues of research :)
Log in to reply
@Calvin Lin – I would still contend that the question seems lacking in definition. Should it be specified that the pyramid must have positive height/volume or it does not count? Is it adequate to assume there can be no flaps when they do not require "cutting or overlapping?" If not, then every regular polygon can be folded into a regular tetrahedron, without cutting nor overlapping. Otherwise, I would change the question to require "just a regular pyramid, nothing less and nothing more," or maybe "no unused area." http://twisty.org/post/folding-polygons-into-pyramids-2
Log in to reply
@Joel Nye – I agree that "2-D folding into 3-D shapes" can be hard to define concretely. I think that the problem is phrased clearly enough to engage with it, and that trying to be more pedantic would be counter productive.
Re: Lemma 1 in your post, can you generalize it further to other kinds of polygons / curves? Hint: An equilateral triangle is formed by 2 equal lengths at 6 0 ∘ .
Log in to reply
@Calvin Lin – I agree it could be further generalized. It may not contribute toward making regular tetrahedrons, but it may have other uses. Conjecture: Any regular polygon of X sides can be inscribed into another regular polygon of sides ≥ X. It strikes me as likely provable, so long as one begins with an axis of symmetry drawn from the midpoint of a side of the outer polygon.
Yes square base pyramid is also possible
An equilateral triangle can be divided into 4 congruent small equilateral triangles (joining the midpoints) and be folded to form a tetrahedron (one kind of pyramid) as shown below: