Polynomial Function

Calculus Level 4

If a non-zero polynomial f ( x ) f(x) satisfies the condition f ( 2 x ) = f ′ ( x ) f ′ ′ ( x ) f(2x) = f'(x) f''(x) , find the value of f ( 3 ) f(3) .


The answer is 12.

Hardik Gupta by Hardik Gupta , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Hardik Gupta
May 12, 2016

Let degree of function = n n
therefore, D E G f ( 2 x ) DEG{ f(2x) } = n n
D E G f ′ ( x ) DEG{ f '(x) } = ( n − 1 ) (n-1)
D E G f ′ ′ ( x ) DEG{ f ''(x) } = ( n − 2 ) (n-2)
so,
n n = ( n − 1 ) (n-1) + ( n − 2 ) (n-2)
=> n = 3 n = 3
let f ( x ) f(x) = a x 3 ax^3 + b x 2 bx^2 + c x cx + d d
=> f ( 2 x ) f(2x) = 8 a x 3 8ax^3 + 4 b x 2 4bx^2 + 2 c x 2cx + d d
also, f ′ ( x ) f '(x) = 3 a x 2 3ax^2 + 2 b x 2bx + c c
and f ′ ′ ( x ) f ''(x) = 6 a x 6ax + 2 b 2b


as f ( 2 x ) f(2x) = f ′ ( x ) f '(x) . f ′ ′ ( x ) f ''(x)
=> 8 a x 3 8ax^3 + 4 b x 2 4bx^2 + 2 c x 2cx + d d = ( 3 a x 2 + 2 b x + c ) ( 6 a x + 2 b ) ) ({3ax^2} + {2bx} + c)({6ax} + {2b}))
by comparing the coeffs.
8 a 8a = 18 a 2 18a^2
=> a a = 4 9 \frac{4}{9}
also, b = c = d = 0 b=c=d = 0
therefore,
f ( x ) f(x) = 4 9 \frac{4}{9} x 3 x^3
therefore,
f ( 3 ) f(3) = 4 9 \frac{4}{9} * 3 3 3^3
=> f ( 3 ) f(3) = 12. 12.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Use \implies for ⟹ \implies symbol.

Samara Simha Reddy - 5 years, 1 month ago

Note that the case of "n=0" has to be dealt with separately, since the degree of the 0 polynomial is not -1.

This is why your solution missed the crucial requirement that the polynomial is "non-zero".

Calvin Lin Staff - 5 years ago
展豪 張
May 13, 2016

Is f ( x ) = 0 f(x)=0 a polynomial too? If so, the answer could be 12 12 or 0 0

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Read question one more time..it's written that if f(x) be a non zero polynomial.

Hardik Gupta - 5 years ago

Log in to reply

I didn't see it when I answer it......

展豪 張 - 5 years ago

Log in to reply

The problem was edited after the "solution" was posted. Those who answered 0 have been marked correct.

In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator who can fix the issues.

Calvin Lin Staff - 5 years ago

Log in to reply

@Calvin Lin – If I have problems with Latex, where I do report it? (Just kidding). I need the codes of Latex because the ones I know uses the $$$ sign. Where can I find helpful hints with latex codes. Thanks.

Hana Wehbi - 5 years ago

Log in to reply

@Hana Wehbi – We use \ ( \ )instead of $ $ to surround Latex. Otherwise, the "codes" are all the same.

You can hover your mouse over the Latex image to see the underlying code.

E.g.

Calvin Lin Staff - 5 years ago

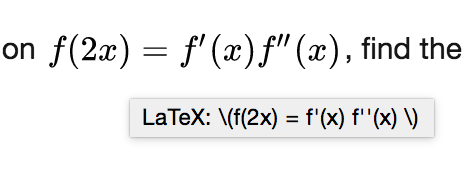
Log in to reply

@Calvin Lin – Thanks, that was really helpful. I will give it a try.

Hana Wehbi - 5 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...