Pool Shark #2
If you have a pool table as shown shaped like an isosceles right triangle, with a ball that starts at the right angle, where should you aim at on the hypotenuse so after one bounce the ball hits the midpoint of the left-hand side of the table?
This problem is part of the Brilliant.org Open Problems Group . The end goal for each open problem is to find a solution, and maybe publish it if it's a nice enough result! You can read about the unsolved billiards problem that this one is related to here .
Assume geometric purity: the "ball" has no mass, the "ball" and "hole" are considered single points, and the ball travels straight.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
You made a mistake, you meant "Since AMP and CPB are similar" instead of "Since AMP and CMB are similar".
This reflection technique is really cool. I also enjoyed the top solution in the Basic section.
How do u know that M is the mid point of AD??
Log in to reply
The goal is the midpoint of AB, and AD is the reflection of AB, and M is the reflection of the goal.
Log in to reply
Thank you so much!!! Nice solution...Keep up the good work.
Relevant wiki: Similar Triangles Problem Solving - Basic
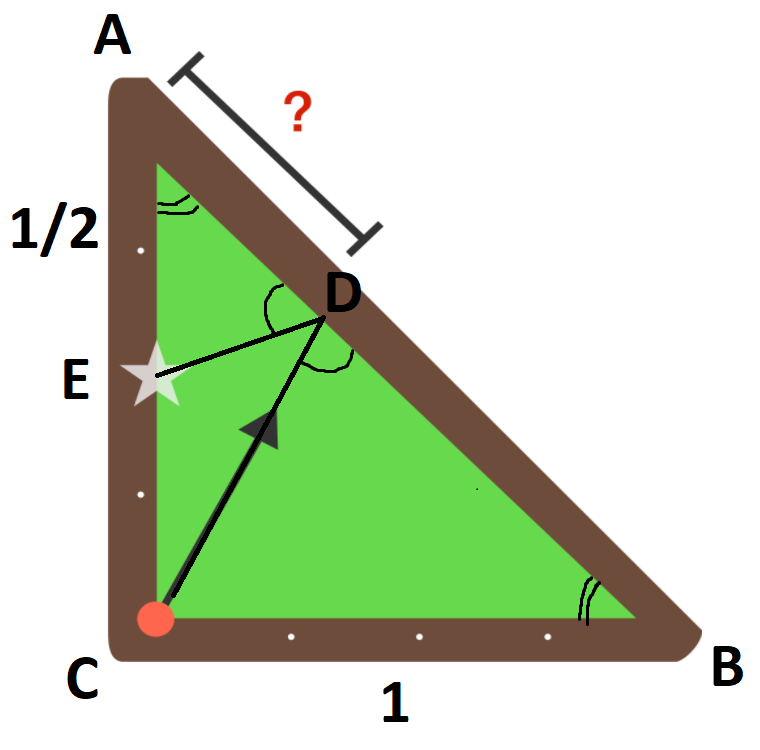
Since the triangle is isosceles, we know ∠ A ≅ ∠ B . Since the ball is reflected back at the same angle after hitting the hypotenuse, ∠ A D E ≅ ∠ B D C . Therefore, △ A D E ∼ △ B D C . Noting that B D = 2 − ? , we set up an equation:
2 − ? ? = 2 1 ⟹ 2 ? = 2 − ? ⟹ ? = 3 2
Therefore, ? is 3 1 of the hypotenuse.
nice solution :) , after you proved △ A D E ∼ △ B D C one could say : since E A = 2 1 C B then A D = 2 1 D B so A B = 3 A D .
Log in to reply
That's a better way of doing it, but I'll keep my solution as it is.
Like the beginning of your slution. Agree with Mehdi, that as soon as it is proved that the triangles are similar, we obtain a ratio of CB:AE. And so can resolve the quiz.
Your question was vague. "along the hypotenuse" does not indicate the starting point. The answer could as easily be 2/3
Log in to reply
The multiple choices also indicate the intent; if 2/3 was also in the multiple choices then there would be ambiguity.
Log in to reply
Plus the "?" segment indicates the starting point is at the top.
This problem assumes that the ball is sliding, not rolling, so the adjustments for moment of inertia falls out of the equation. That rules out both lateral spin (what billiards players call "English") and radius effects (so we have a point ball rather than a physical object). The latter would make the answer slightly larger than 1/3. The former could substitute literally any answer by controlling the magnitude and direction of the spin on the ball.
Log in to reply
I added a comment about assuming geometric purity for the purposes of this problem (watch this space, though - we have "real billiards table" problem for next week).
What exactly is radial effects? I mean if it is spinning, along velocity, from top to bottom or bottom to top won't it give different answers?
Log in to reply
I said "radius" not "radial" -- the target varies based on the size of the ball. The answer given assumes size zero.
 Reflect the goal in the longer side (hypothenuse), and draw a line from the start position to the goal's reflection. Consider the set of equidistant parallel lines as shown in the diagram. Such lines divide any intersecting line in equal parts. It is then clear that the desired segment is
\fbox{\$\frac{1}{3}\$}
of the longer side.
Reflect the goal in the longer side (hypothenuse), and draw a line from the start position to the goal's reflection. Consider the set of equidistant parallel lines as shown in the diagram. Such lines divide any intersecting line in equal parts. It is then clear that the desired segment is
\fbox{\$\frac{1}{3}\$}
of the longer side.
this is art
Would've been my approach, too. Makes sense to pool/snooker players!
The star in the reflection is not representing the half any more. Agreed with the visual representation, it was the simplest in my mind as well. Thanks!
Log in to reply
What do you mean? The stars label the midpoint on both sides. The slanted lines create an optical illusion.
how do we know the parallel lines are all equidistant?
Log in to reply
Create a grid of the squares. Then the parallel lines alternate passing through one corner and one midpoint. Their horizontal distance is half the width of the square.
The question was poorly written... along what from where?
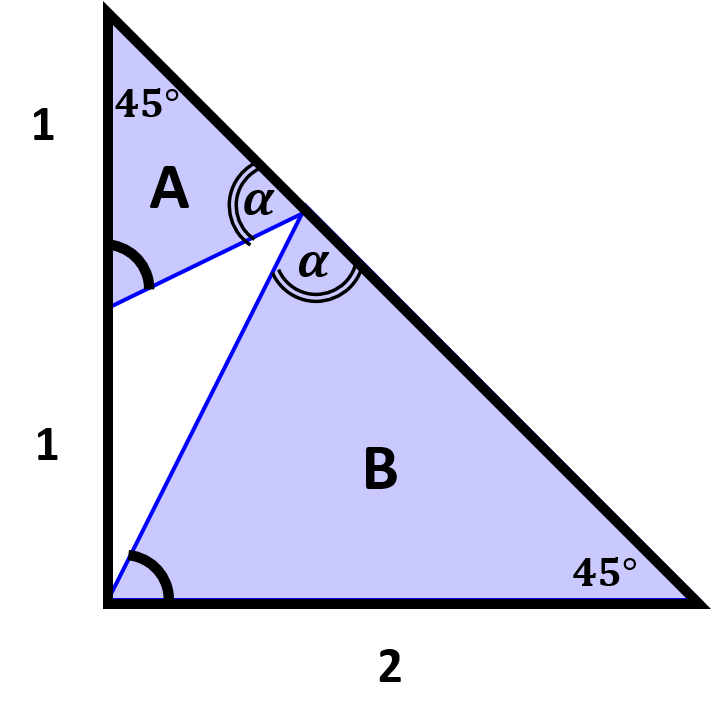
Assuming no trick-shot spin, the ball must bounce of the hypotenuse of the triangle with equal incident-reflection angles (alpha) in the diagram below.
Simple geometry shows that triangle A and B in diagram have same proportions and B is 2 x size of A (length dimensions). Therefore the hypotenuse of the original triangle must be divided by ratio 1:2 or 1/3 : 2/3.
Perfect simple solution!
Applying the same principle of following a line across adjoining reflected tables used in a solution of the 2 bounce center to upper right corner problem.
I got a really easy intuitive solution without maths: Imagine a line parallel to the hypothesis going through the starting point. Then imagine the square with the goal point in its centre. Now complete the path the ball goes in this square so that the path goes through the goal and ends in the corner opposite to the starting corner. The 3 straight segments of this path obviously have the same length. As well as the shadow they throw on the hypothesis. So it's obvious the aim-point is at 2/3 of the side of the square, which is 1/2 of the hypothesis. 2/3 * 1/2 = 1/3
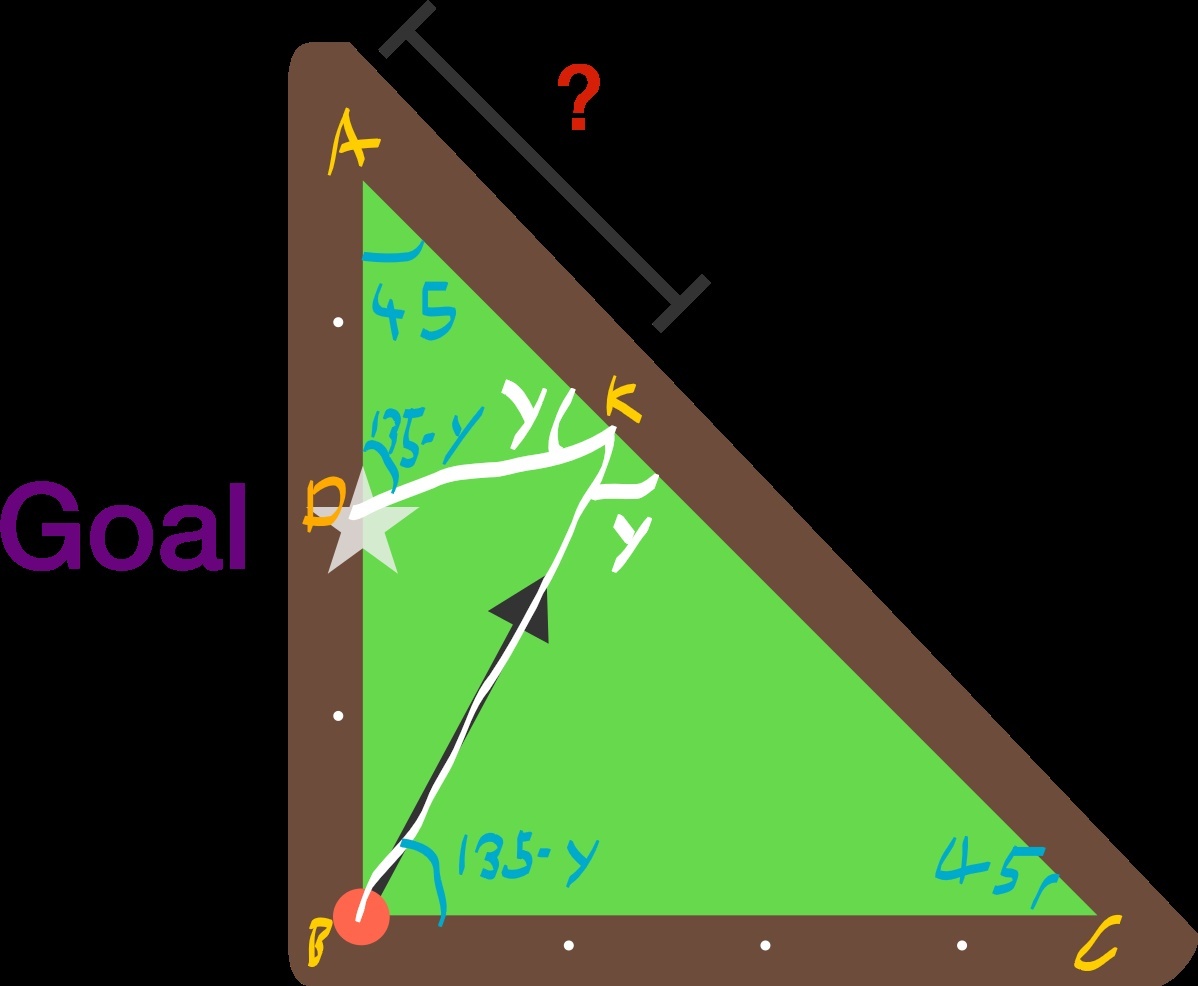
Since D is the center of segment A B , assign A B = 2 . Therefore, A D = D B = 2 1 . ∠ A B C = ∠ A C B = 4 5 ∘ . △ A D K and △ C B K are similar, as their angle measures are the same. This means that A K A D = C K C B . But B C A D = 2 1 , then C K A K = 2 1 , meaning that C K A K = 3 1
Go play pool for a while and you will know that it is about 1/3 down.
Let the triangle vertices be A,B,C, where A is at top and B is the right angle. Let D be the mid-point of the left side, P be the point on the hypotenuse where the ball strikes, and <t = <BPC = <APD, by the reflection law. Let S be a side, S sqrt(2) the hypotenuse, and x = AP. We have the following equations by the Law of Sines: (1) (S/2)/sin(t) = x/sin(135 -t), and (2) (S sqrt(2) - x)/sin(135 - t) = S/sin(t). Substituting, 2x = S sqrt(2) - x, and x = (1/3)S sqrt(2) = (1/3)*hypotenuse. Ed Gray
You do not need fancy maths to solve this problem. Let the Goal be point G. Let the bounce point on AC be D. Let the angle BDC be alpha. If no energy is lost in the bounce then the angle ADG will also be alpha. Angles GAD and DCB are both 45 degrees. So, triangles AGD and BDC are similar triangles. AG is opposite angle ADG (alpha). BC is opposite angle ADG (alpha). BC is twice as long as AG. So, DC is twice as long as AD. So AD is one third as long as AC. So you should aim the ball to hit AC one third of the way between A and C. It takes longer to explain than it does to work it out in your head.
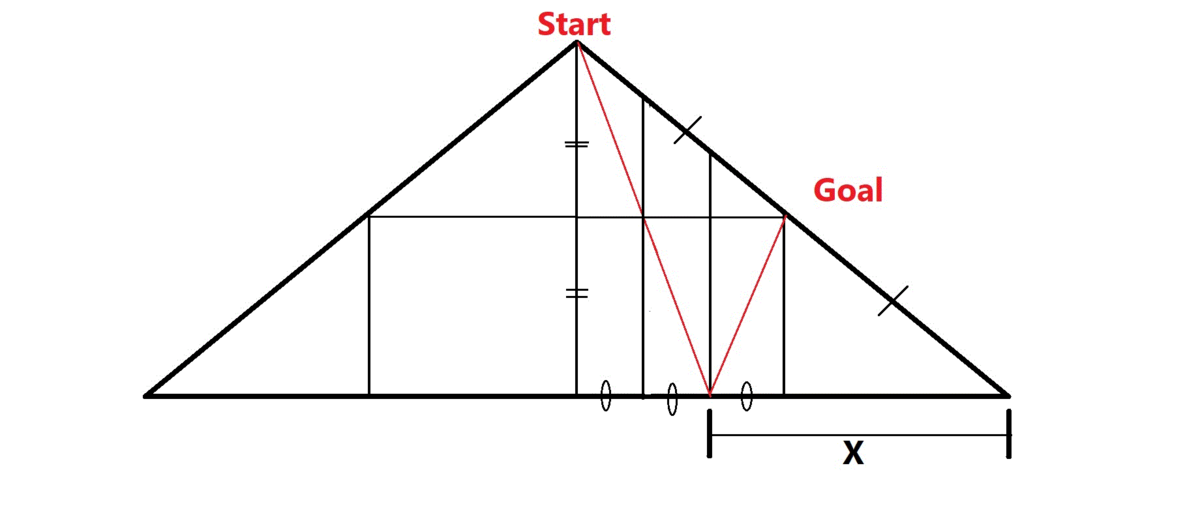
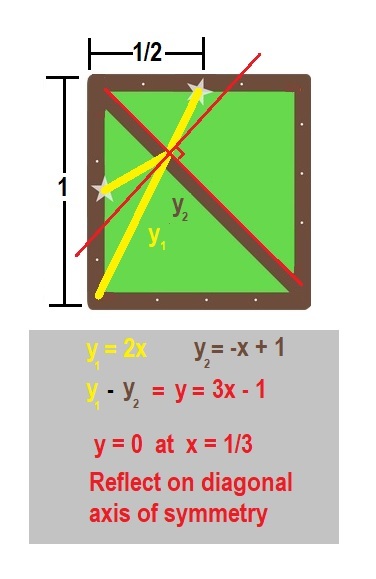
As shown above, reflect the table over the diagonal line to achieve a square.
What you now need to do is aim at the reflected midpoint, M.
Since AMP and CPB are similar with ratio AM:CB=1:2, we achieve AP:CP=1:2, leading to AP= 1/3 AC.