Poor Bug, Will it ever succeed?
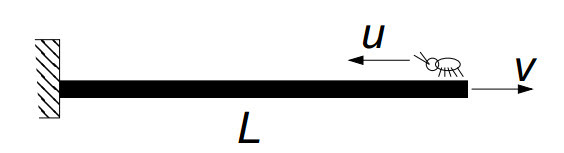 An extremely stretchable rubber band of natural length
L
has its one end tied to a wall.
An extremely stretchable rubber band of natural length
L
has its one end tied to a wall.
A bug peacefully rests at the outer end. Just when it seemed that everything was good, an evil-minded child starts pulling the outer end by a constant velocity
v
. The bug immediately realizes the danger, and simultaneously starts crawling towards the other end at a speed
u
(relative to the band).
Will the bug ever reach the wall? If so, how long (in sec) would it take to reach it?
Answer 0 if you think that the bug will never reach the wall.
Details and Assumptions:
∙
L
=
1
5
cm
∙
v
=
3
cm/s
∙
u
=
1
cm/s
The answer is 95.427.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How to solve that differential equation?
shouldn't it be -(u+v) instead of -u, as it is given relative to the band it is u
speed of stretching at bug position vx/(L+vt) how????????
Log in to reply
Speed varies linearly along the band....
In other words, the speed at the tied end is zero, and the speed at the free end is
v
,
So since the band stretches uniformly, the speed at a general position on the band (measured from the tied end) is given by,
v s t r e t c h = v l e n g t h x
Now, note that the length of the band is varying with time as,
l
e
n
g
t
h
=
L
+
v
t
Hence.
v
s
t
r
e
t
c
h
=
v
L
+
v
t
x
Log in to reply
But, you didn't mention uniform stretching in the question. I assumed all the points on band to be moving with 3cm/s.
Log in to reply
@Shubham Maurya – Then how will the point at the wall move? That proves that you are wrong...
Log in to reply
@Kishore S. Shenoy – yeah I got it now..Thanks
Log in to reply
@Shubham Maurya – I'm happy that I became useful
awesome solution !! truly brilliant
we can also consider fraction of band covered f then df/dt=u/(L+vt) then integrate f from 0 to 1 hence the answer.
How do you solve a differential equation of that type? (I'm young :P) I got stuck there so I tried another approach, evaluating the fraction x(t)/l(t) where x(t) is the distance of the bug from the wall and l(t) is the position of the rubber band at time t. Then I evaluated that fraction at time t+dt, and it allowed me to get an easy ode after approximating to first order in dt (there was a +vdt in a denominator summed to L+vt)
Log in to reply
Substitute. That will work. Please ask if I'm not clear.
the bug can never reach the wall because in frame fixed to the other end of the rubber band the wall appears to be moving at velocity greater than the bug so how can these to reach wall will always a ahead of the bug
x ˙ = 1 5 + 3 t 3 x − 1 = 5 + t x − 1
x ˙ − 5 + t x = − 1
x ˙ + f ( t ) x = g ( t )
The integrating factor is e ∫ f ( t ) d t = e ∫ − 5 + t d t = e − ln ∣ t + 5 ∣ = t + 5 1
Multiplying the whole equation by the integrating factor.
t + 5 x ˙ − ( t + 5 ) 2 x = t + 5 − 1
∫ [ t + 5 x ˙ − ( t + 5 ) 2 x ] d t = ∫ t + 5 − d t
t + 5 x = ∫ t + 5 − d t
t + 5 x = − ln ( t + 5 ) + C
Putting t = 0 and x = 1 5 gives C = 3 + ln 5 .
t + 5 x = − ln ( t + 5 ) + ln 5 + 3 = ln t + 5 5 e 3
x = ( t + 5 ) ln t + 5 5 e 3
Solving x = 0 gives t = 9 5 . 4 3 .
Let x be the distance of the bug from the wall. dx/dt = u + [x/(L+vt)]v
Consider the auxiliary variable z = x/(L+vt). Using this new variable leads to: d/dt[(L+vt)z]=u+vz
or
(L+vt)dz/dt + vz = u + vz
or
dz = u dt/ (L+vt)
Integrating both sides yields z(t) = (u/v) ln [1+vt/L]
By using the condition z=1 when the beg reaches the end of the rubber band, we can get the fllowing through elementary algebra:
t = (L/V) [ exp(v/u) -1] = 5 ( e^3 - 1) = 95.4276846 s
Consider coordinate ψ measured along the band, with the starting fixed point ψ = 0 , and the end point ψ = 1 . In this system, all points on the system remains fixed (in terms of ψ ) as the ropes stretches. A point x = X on the the rope will have a coordinate ϕ ( t ) = ψ = L + v t X , and the speed of the bug is equivalent to ϕ ′ ( t ) = − L + v t u
We thus reduced the requirement of solving the Difference Equation.
So, ϕ ( t ) = − v u ln ( L + v t ) + κ where κ is the constant of integration.
Putting limits to get the value of κ , we know ϕ ( 0 ) = 1 1 κ ⇒ ϕ ( t ) = − v u ln L + κ = 1 + v u ln L = − v u ln ( L + v t ) + 1 + v u ln L = v u ln ( L + v t L + 1 )
Hence, to get time T , ϕ ( T ) = 0 ⇒ 1 ⇒ T = v u ln ( L + v T L + 1 ) = v u ln ( L L + v T ) = v L ⎝ ⎛ e u v − 1 ⎠ ⎞
∴ T = v L ⎝ ⎛ e u v − 1 ⎠ ⎞ ≈ 9 5 . 4 2 7 7
Moderator note:
Good standard solution. Can you think of a way to the answer without solving differential equations?
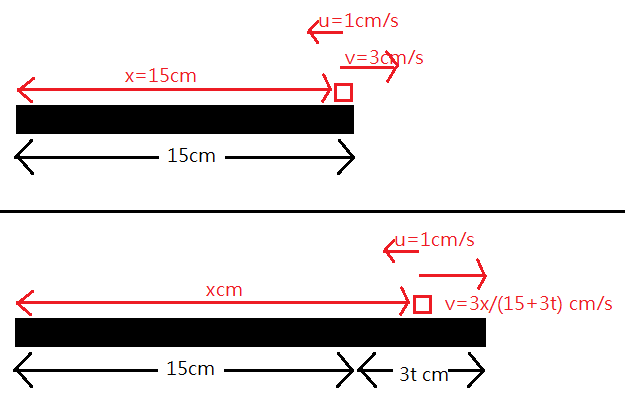
Assume at time t , the bug is at a distance x from the wall.
At the same time, the free end of the rubber band is at a distance L + v t from the wall.
Since the band stretches uniformly,
The speed of stretching at the position of the bug is,
v L + v t x
Thus, the relative velocity of the bug with respect to the wall is,
v L + v t x − u = d t d x
Solving the differential equation, and substituting x = 0 , we get,
t = v L ( e v / u − 1 ) ≈ 9 5 . 4 2 7 s e c